近年来泥沙数学模型要求不仅要能够计算沿程冲淤和总含沙量沿程变化,还要能够计算悬沙与床沙的级配组成及其变化。为此,就必须建立非均匀沙分组输沙能力的计算方法。何明民和韩其为在研究非均匀悬移质不平衡输沙时引进了输沙能力级配的概念,认为一般条件下,输沙能力级配不仅取决于床沙级配,而且还与含沙量级配有关。并且证明,在明显淤积条件下,淤积物级配即为有效床沙级配,含沙量级配即为输沙能力级配。......
2023-06-22
在上述四类方法中,目前还没有一种方法能够给出令人满意的分组输沙能力计算结果。直接分组计算法的结果精度最差,在数学模型中已较少采用;剪切力修正法在推移质分组输沙能力计算中采用较多,该类方法的研究思路和方法应该可以延伸到床沙质分组输沙能力计算中;床沙分组法由于计算简单,在数学模型中应用广泛,但不论是剪切力修正法还是床沙分组法,计算的分组及总输沙能力都不能够令人满意;输沙能力级配法的优点在于能够避免采用分组输沙能力求和计算总输沙能力时带来的误差,并将分组输沙能力的误差控制在一定范围内,此外,还可以将剪切力修正法中考虑隐蔽作用的思路引入到输沙能力级配函数Pci的计算中,从而考虑不同粒径组泥沙对分组输沙能力的影响。下面就基于输沙能力级配法的概念,并考虑粗细颗粒泥沙的掩蔽和暴露作用,建立一种分组输沙能力计算方法。
2.4.3.1 输沙能力级配函数
输沙能力级配法的分组输沙能力计算由两部分组成:一是床沙质总输沙能力Ct;二是输沙能力级配函数Pci。理论上讲,Ct和Pci是相互关联的,但为了简便起见,一般假定这两部分可以分开考虑。
输沙能力级配函数Pci与床沙级配Pbi既有区别又有联系。两者的区别表现在前者是输沙平衡状态下水流中输移泥沙的级配,后者是基本处于静止的河床泥沙的级配,而且前者的泥沙级配较后者为细(吴保生和马吉明,2002)。两者的联系则体现在水流中输移泥沙通过与床面泥沙的不断交换,对河床泥沙有很强的依赖性,这也正是床沙分组法及式 (2-77)表示的剪切力修正法将床沙级配Pbi看作泥沙在河床上的补给率的依据。
考虑到输沙能力级配函数与床沙级配的联系,可以以床沙级配Pbi表示的床沙补给率为基础,首先依据床沙分组法的概念得到输沙能力级配函数的第一近似。为此,Yang的无量纲单位水流功率公式(Yang& Molinas,1982)可以简化为:
![]()
式中:a和b 分别为系数和指数,它们与水流和泥沙特性有关;ω50为相应于粒径D50的泥沙沉速。
根据床沙分组法的概念,第i粒径组泥沙的床沙质含沙量可表示为:
![]()
将式(2-83)和式(2-84)代入式(2-82)得到:
![]()
式 (2-85)与窦国仁等 (1987)提出的悬移质输沙能力级配公式相似,可以作为非均匀沙输沙能力级配的初步近似。图2-17点绘了Pcmi/Pbi随ωi/ω50的变化情况,图中包括了共118组实测数据 (见表2-9)。由图可以看到,除了采用原始泥沙级配代替床面表层泥沙级配的Samaga等的数据之外,Pcmi/Pbi与ωi/ω50之间存在一定的趋势关系。但值得注意的是,它们之间的关系难以用一个简单的幂函数来表示。较小的细颗粒泥沙由于受到较大的粗颗粒泥沙的隐蔽作用,相应的挟沙能力变小;较大的粗颗粒泥沙受到的水流动力作用较它们在均匀沙条件下所受作用力增大,相应的挟沙能力变大。此外,在水流功率小、剪切力小的情况下,特别粗的粗颗粒泥沙可能根本就不会产生运动,出现所谓的部分输沙现象。

图2-17 Pcmi/Pbi随ωi/ω50的变化情况
(a)Einstein水槽资料;(b)Einstein 和Chien水槽资料;(c)Samaga等水槽资料;(d)Niobrara和Loup河资料
前面提到的理论分析指出,较小颗粒所受的隐蔽作用以及粗颗粒所受的暴露作用主要依赖于相对粒径的大小 (Einstein,1950;Misri等,1984;White&Day,1982;Proffitt&Sutherland,1983;Karim&Kennedy,1981),例如Dsi/X、Dsi/D50、Dsi/DA、Dsi/Du和Dsi/Da。与这些相对粒径相似,下面采用ωi/ω50来表示非均匀沙中其余粒径组对某一粒径组的隐蔽与暴露作用,这样可以在式(2-85)的基础上引入表示隐蔽与暴露作用的修正项,由此得到:
![]()
式中:C1和C2为系数;α和β 为指数。
定性地讲α应该是一个负值,结果使得细颗粒泥沙的Pci大于Pbi;而对于粗颗粒泥沙,Pci小于Pbi。如果β取大于零的正值,则对于细颗粒泥沙,式(2-86)中第二项将得出一个较小值;而对于粗颗粒泥沙,式(2-86)中第二项将给出一个较大值。结果,第二项能够补偿第一项对细颗粒输沙能力的过高估计以及对粗颗粒输沙能力的过低估计。也就是说,第二项反映了非均匀沙的隐蔽与暴露作用。
式(2-86)中的ω50可看作是相应于尺度粒径的沉速,实际沉速小于ω50的颗粒受到隐蔽作用,大于ω50的颗粒受到暴露作用。考虑到ω50对应的不一定正好是隐蔽与暴露作用的分界粒径,在更一般的情况下式(2-86)可表示为:
![]()
式中:ωn为相应于尺度粒径的泥沙沉速。把式 (2-82)作为式 (2-87)的约束条件,可得到Pci的如下基本表达式:
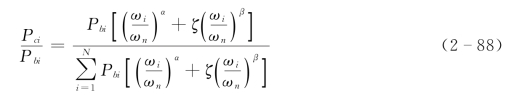
式中:ζ=C2/C1。
为了反映泥沙级配的影响,床沙的尺度粒径可定义为:
![]()
则床沙的尺度粒径所对应的沉速为:
![]()
式中:σg= D84/D16为床沙的几何标准差;D84和D16分别为床沙中以重量计84%和16%较之为小的粒径。
河床上泥沙所受的隐蔽与暴露作用与床面形态的大小、运动速度及河床泥沙的粒径范围有关。随着水流强度的增加,紊动作用加强,隐蔽与暴露作用变成次要因素,所以式(2-88)中的系数和指数不应是常数,而是随水流强度和泥沙特性的变化而变化,可以表示为如下的一般函数关系:
![]()
式中:h 为平均水深;U 为平均流速;Fr为弗劳德数。
式(2-91)中系数和指数的具体表达式需要根据实测输沙数据来确定。为此,选择了实验室水槽和野外实测资料共计118组,891个数据点,见表2-9。这些数据包括Einstein (1978)、Einstein和Chien (1953)、Samaga等(1986a,b)的水槽试验数据,以及从Nebraska州Cody附近的Niobrara河(Colby& Hembree,1955)和位于Nebraska州Dunning的Loup河中游测得的野外实测数据。基于对上述数据的分析,得到α、β和ζ 的具体表达式如下:
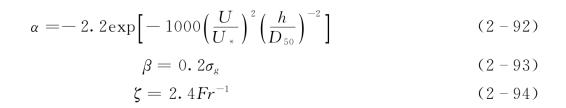
表2-9 实验室水槽数据和野外实测数据汇总表
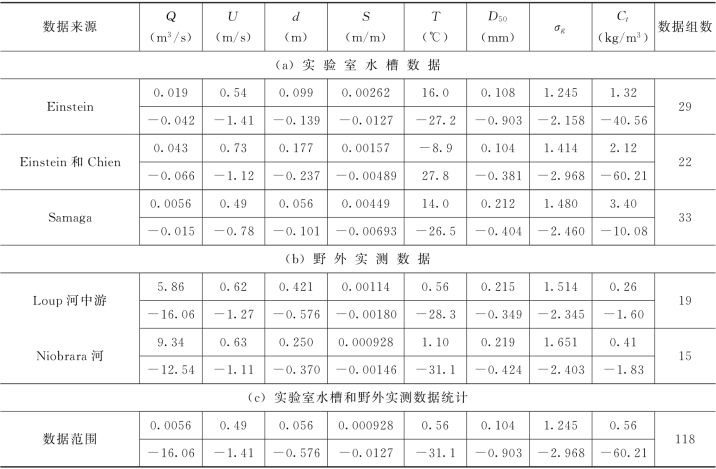
如果以Engelund-Hansen (Engelund& Hansen,1967)公式为基础,经过与式 (2-83)~式(2-88)相似的推导过程,便可以得到以Di/D50表示的挟沙能力级配函数:
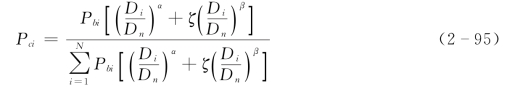
相应系数和指数的表达式为:

式(2-92)和式(2-96)中α的绝对值随着(U/U*)2(h/D50)-2的增大而减小,这意味着Pci/Pbi的变化范围随水流强度的增大而减小,这是因为在水流强度较大时不同粒径组泥沙的可动性更加接近。式(2-93)和式(2-97)中β的值随着σg的增大而增大,说明粗颗粒对细颗粒的隐蔽作用和粗颗粒在床面上的暴露程度随σg的增大而增强。式(2-94)和式(2-98)中ζ的值随着Fr 的增大而变小,这表明随着水流强度的增加,床沙的不均匀性带来的影响在变小。
2.4.3.2 Ct的计算方法
虽然原则上Ct可以选用任何床沙质公式确定,但Ct计算的精确程度影响所有分组输沙能力的大小,从而影响分组输沙能力的预报精度,需要认真对待。
Molinas和 Wu (1998)曾对Engelund-Hansen (1967)公式、Ackers-White(1973)公式、Yang (1973)公式用于计算非均匀沙的床沙质输沙能力的精度进行了分析,认为仅仅选用某一固定不变的特征粒径如D35或D50作为床沙代表粒径来计算床沙质输沙能力时,这个固定不变的粒径不能够反映泥沙的非均匀性对挟沙能力大小的影响。为此,Molinas和Wu提出了一个所谓的床沙等效代表粒径,应用于Engelund-Hansen公式、Ackers-White公式、Yang公式,以修正因采用单个固定不变代表粒径对计算结果带来的偏差。Molinas和Wu提出的等效代表粒径的具体表达式如下:

相应的等效代表沉速为:
![]()
采用式(2-99)表示的等效代表粒径De(或是相应的ωe)代替Engelund-Hansen公式、Ackers-White公式、Yang公式中的代表粒径(或代表沉速),便可以得到考虑床沙非均匀性修正的床沙质输沙能力。
2.4.3.3 各种方法计算结果的比较
下面就以上建立的分组输沙能力计算方法与以往一些具有代表性的方法进行比较。所选方法包括:①直接分组计算法中的Einstein 公式 (1950)、Laursen 公式 (1958)和Toffaleti公式(1968,1969);②采用Engelund-Hansen (1967)公式、Ackers-White(1973)公式和Yang (1973)公式的床沙分组法,以及Karim (1998)修正床沙分组法;③基于输沙能力级配法的方法则是采用Engelund-Hansen (1967)公式计算总输沙能力,采用Karim 和Kennedy (1981)、李义天 (1988)的输沙能力级配函数计算输沙能力级配。考虑到多数基于剪切力修正法的分组输沙能力计算方法只适用于卵石河床,下面的比较中不包括此类方法。
根据输沙能力级配函数式(2-88)计算的输沙能力级配与实测值之间的比较见图2-18。可以看到,式(2-88)计算的Pcmi值与实测值Pcci之间还是比较吻合的,尤其是在Pcmi值较大时。使用式(2-88)与采用De的Engelund-Hansen公式计算分组输沙能力结果如图2-19所示,可以看到,建立的分组输沙能力计算结果基本合理。此外,采用式(2-88)和式(2-95)与Ackers-White公式或Yang公式也可以得到与图2-19类似的结果。

图2-18 输沙能力分布函数式 (2-88)计算分组输沙能力百分数与实测值之间的比较

图2-19 输沙能力级配法计算分组输沙能力与实测值之间的比较
[采用以De作为代表粒径的Engelund-Hansen公式计算Ct,采用输沙能力级配函数式(2-88)计算Pci]
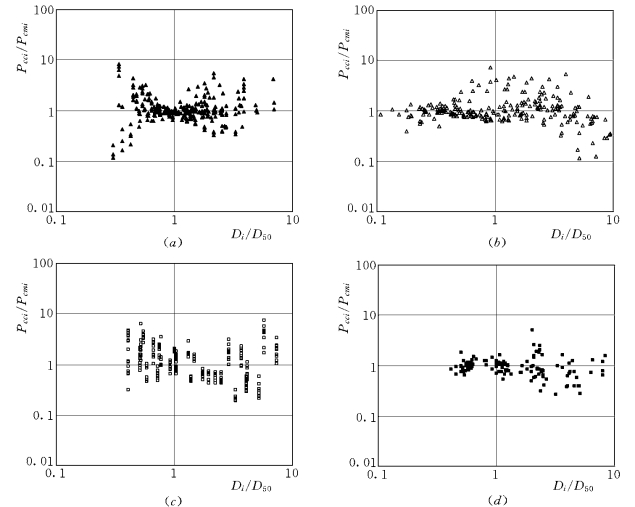
图2-20 采用输沙能力级配函数式 (2-88)计算得到的Pcci/Pcmi随Di/D50的变化情况
(a)Einstein水槽资料;(b)Einstein 和Chien水槽资料;(c)Samaga等水槽资料;(d)Niobrara和Loup河资料
图2-20点绘了Pcci/Pcmi[式(2-88)计算输沙能力级配Pcci与实测床沙质输沙率级配Pcmi之比]随Di/D50的变化,图中的Pcci/Pcmi等于1表示计算值与实测值完全一致。可以看到,大部分的点据都落在Pcci/Pcmi等于1附近。
作为其他方法的代表,图2-21和图2-22给出了Einstein方法和基于Engelund-Hansen公式的床沙分组法所得Pcci/Pcmi随Di/D50的变化。可以看到,较细颗粒和较粗颗粒泥沙的计算结果都很分散,当粒径接近于D50时,Pcci/Pcmi的比值才会比较接近1。
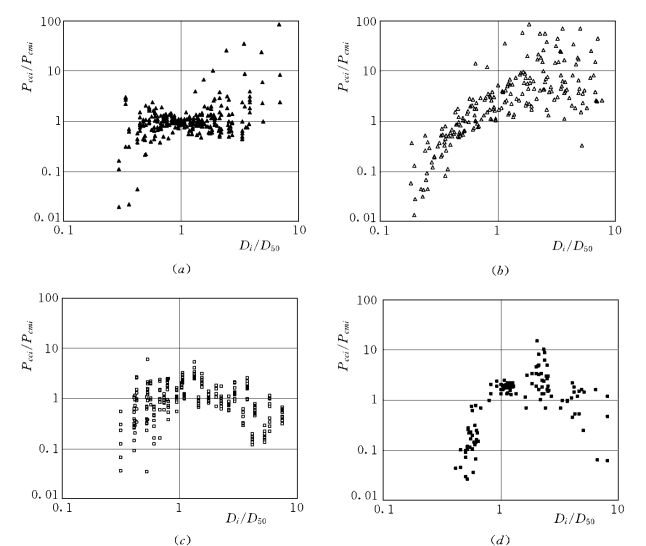
图2-21 采用Einstein方法计算得到的Pcci/Pcmi随Di/D50的变化
(a)Einstein水槽资料;(b)Einstein和Chien水槽资料;(c)Samaga等水槽资料;(d)Niobrara和Loup河资料
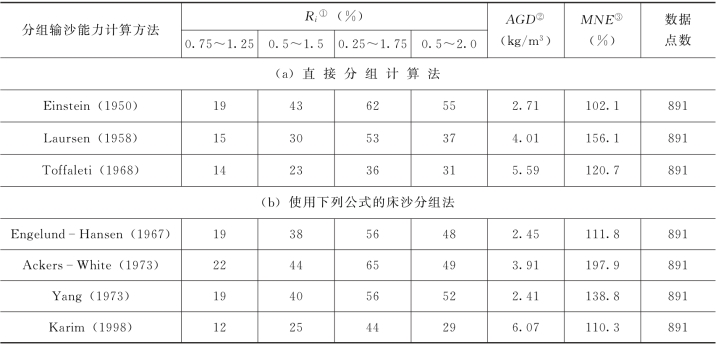
采用不同方法计算所得分组含沙量与实测分组含沙量之间的比较结果见表2-10。表中采用了3种不同的统计方法,包括偏差比Ri、平均几何偏差AGD、平均标准差MNE,每个统计参数从不同侧面说明了计算结果与实测值之间的吻合程度。3 个统计参数Ri、AGD、MNE 均表明,采用式(2-88)和式(2-95)表示的输沙能力级配法函数,得到的分组床沙质输沙能力的结果最好,采用Karim 和Kennedy的输沙能力级配法函数给出的结果也与实测值较为接近。总的说来,直接计算法中的Laursen公式和Toffaleti公式、基于床沙分组法概念的Ackers-White方法和Karim 方法以及基于输沙能力级配法的李义天输沙能力级配法函数给出的计算误差最大,Einstein方法及使用Engelund-Hansen公式和Yang公式的床沙分组法给出的结果稍好些。

图2-22 基于床沙分组法的Engelund-Hansen公式计算Pcci/Pcmi随Di/D50的变化
(a)Einstein水槽资料;(b)Einstein 和Chien水槽资料;(c)Samaga等水槽资料;(d)Niobrara和Loup河资料
表2-10 计算分组含沙量与实测分组含沙量之间的比较结果汇总表
续表
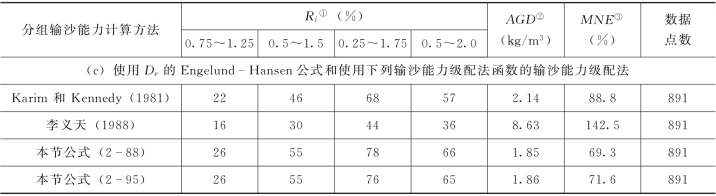
① Ri=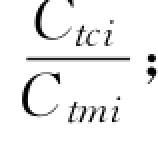 ;
;
② 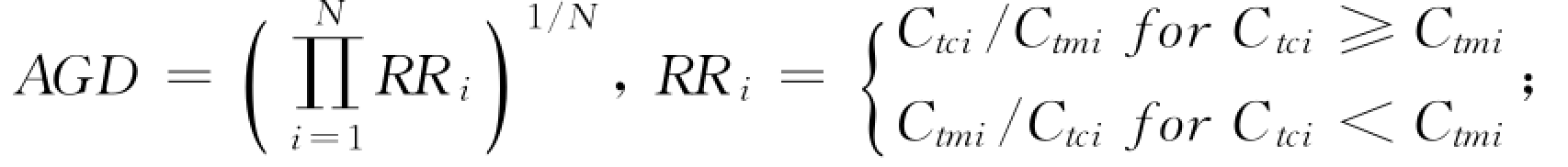
③ 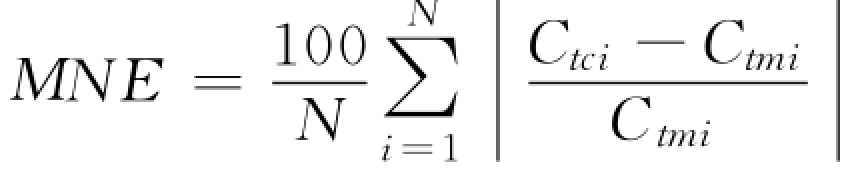 。
。
有关泥沙研究进展的文章

近年来泥沙数学模型要求不仅要能够计算沿程冲淤和总含沙量沿程变化,还要能够计算悬沙与床沙的级配组成及其变化。为此,就必须建立非均匀沙分组输沙能力的计算方法。何明民和韩其为在研究非均匀悬移质不平衡输沙时引进了输沙能力级配的概念,认为一般条件下,输沙能力级配不仅取决于床沙级配,而且还与含沙量级配有关。并且证明,在明显淤积条件下,淤积物级配即为有效床沙级配,含沙量级配即为输沙能力级配。......
2023-06-22

目前比较典型的分组交换数据网有DATAPAC、CHINAPAC、TRANSPAC等。X.25是一组协议,于1976年3月正式成为国际标准,规定了分组终端与分组交换网的接口规程。......
2023-10-22

分组转发又称为分组交付,是指互联网中路由器转发IP 分组的物理传输和转发交付机制。当IP 分组到达与目的主机所在网络的路由器时,进行直接交付,随后分组到达目的主机,在中间路由器的存储转发过程结束。图6.8未划分子网的分组转发以路由器R2 的路由表为例,其路由表中的表项如图6.8所示。图6.9划分子网的分组转发路由器R1 收到这个分组后,就在其路由表中逐行寻找有无匹配的网络地址。......
2023-10-19

碳足迹是指企业机构在生产活动过程中,或个人在食、住、行、游、购、娱等过程中排放的温室气体数量的总和。我们知道,煤炭、石油、木材等自然资源都是由碳元素构成的,所以,我们使用的资源越多,“碳足迹”就越大。有的碳足迹计算器可以计算我们在衣、食、住、行等多个方面的排放量。......
2023-06-21

Einstein 认为,水流的输沙能力与水流克服沙粒阻力所要求的能坡J′有关,而不是总能坡J。式表示的关系式与Velikanov、张瑞瑾、窦国仁分别提出的式 (2-2)、式(2-4)、式(2-5)表示输沙能力关系的形式基本相同。因此,在大河流的输沙能力计算公式中,选择合适的阻力公式,将比降表示为速度和水深的函数,是一种较为有效的处理办法。根据表2-1给出的414组大河流输沙资料点绘了Ct与Ψ 的关系,见图2-4。......
2023-06-22

转子发动机正常工作时受到的机械载荷分别为装配过程的螺栓预紧力以及气体燃烧的爆发压力。根据材料力学公式3.单个螺栓的总载荷气缸盖螺栓受到总拉力根据以上公式,代入相关的参数值后可以计算求得螺栓预紧力。图3.21气缸螺栓预紧力分布情况气体压力的施加方式与温度-对流换热系数的施加方式相同,需根据转子发动机实际工作特点划分区域。图3.22各转速缸内压力图3.22各转速缸内压力......
2023-06-23

图5.15分组交换网示意图值得注意的是,X.25分组交换网是产生于20世纪70年代的第一个商用的分组交换网,本节所讲述的分组交换的概念及技术等,都是基于X.25分组交换网的。图5.16表示分组交换节点在路由选择中的工作原理。......
2023-06-26
相关推荐