修正因子检验的优化方法

2023-06-22 理论教育版权反馈

【摘要】：由于Engelund-Hansen公式是针对粒径相对均匀的沙质河床而建立的，所以Kd修正的适用性应采用沙质河流中具有较大σg值的非均匀沙资料进行检验。表2-5用于检验Kd修正的水槽试验和天然河流资料情况由此得到式中的b值为1.2。由此可以认为，对σg小于1.5的数据，修正因子Kd对输沙率的修正可以忽略，而对σg大于2的数据，计算精度则显著提高。

pagenumber_ebook=80,pagenumber_book=64

图2-11　分组输沙能力随相对粒径的变化

图2-11点绘了所选水槽试验和天然河流资料的相对分组输沙率或输沙能力随相对粒径的变化趋势，图中各粒径组相对输沙能力的计算步骤见表2-4。表中Dk、ΔPbk、Qsk均为实测值，Qspk则是按Qsk/ΔPbk的计算结果。

表2-4　相对输沙率计算举例

pagenumber_ebook=81,pagenumber_book=65

注 1.表中数据摘自Einstein和Chien水槽试验的第22组试验资料;
2.D50=0.135mm;
3.(5)= (4)/ (3);
4.Qsp50是对应于D50的可能输沙能力。

由图2-11可以看到，相对输沙能力随着泥沙粒径的增大而减小。图中所示资料的这种趋势曲线可表示为:

pagenumber_ebook=81,pagenumber_book=65

由此得到式(2-43)中的b值为1.2。一般来讲，b值应随泥沙粒径和水流强度的变化而变化，并呈现出非线性的变化关系，但为简单起见，这里暂取为常数。

由于Engelund-Hansen公式是针对粒径相对均匀的沙质河床而建立的，所以Kd修正的适用性应采用沙质河流中具有较大σg值的非均匀沙资料进行检验。可以预料，按Engelund-Hansen公式计算的输沙能力将会偏低。通过Kd来反映床沙非均匀性的影响，能给出更符合实际的计算结果。

对于沙质河床，尽管不乏水槽试验和天然河流输沙资料，但含有相对较高σg值的资料不多。经过仔细筛选，选用了Einstein 和Chien (1953)和Samaga等 (1986a，b)的水槽试验资料，以及Atchafalaya 河 (Toffaleti，1968)、Mississippi 河 (Toffaleti，1968)、Rio Grande河(Toffaleti，1968)和美国运河 (Simons，1957)的野外资料，见表2-5。Einstein 和Chien及Samaga等人的水槽试验资料中，σg值分别在1.4～3.0和1.6～2.5范围内，绝大部分数据点大于2;D50的值则分别在0.10～0.37mm 和0.21～0.40mm 范围内。Atchafalaya河、Mississippi河、Rio Grande河和美国运河的野外资料中，σg的值则分别在1.5～1.9、1.4～2.0、1.6～1.9 和2.0～3.9 范围内，D50值在0.091～0.31mm、0.178～0.327mm、0.214～0.387mm 和0.096～0.715mm 范围内。

表2-5　用于检验Kd修正的水槽试验和天然河流资料情况

pagenumber_ebook=82,pagenumber_book=66

取σg等于1.5、2、2.5 和3，由式(2-49)得到Kd值依次为1.08、1.41、1.83和2.38。由此可以认为，对σg小于1.5的数据，修正因子Kd对输沙率的修正可以忽略，而对σg大于2的数据，计算精度则显著提高。

采用Kd修正所得结果与实测值的比较见表2-6 (水槽试验资料)和表2-7 (天然河流资料)。表中采用了三个统计参数来表示计算和实测结果的吻合程度，分别是偏差比、几何标准差和均方根。偏差比的定义见式(2-20)，几何标准差和均方根的定义如下:

几何标准差:

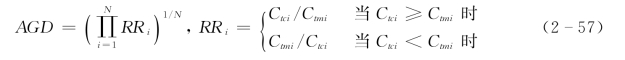
pagenumber_ebook=82,pagenumber_book=66

表2-6　水槽试验数据的计算和实测床沙质含沙量的比较结果

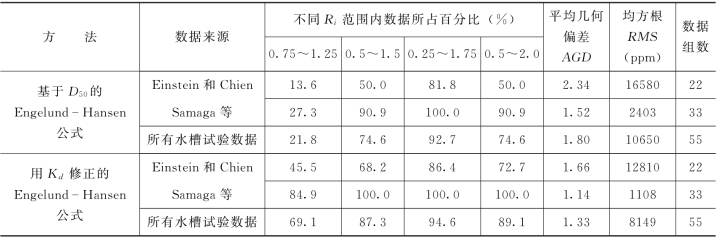
pagenumber_ebook=82,pagenumber_book=66

表2-7　天然河流数据的计算和实测床沙质含沙量的比较结果

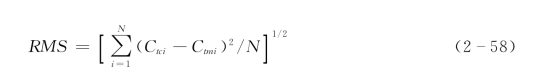
pagenumber_ebook=83,pagenumber_book=67

均方根:

pagenumber_ebook=83,pagenumber_book=67

式中:Ctc和Ctm分别为计算和实测的床沙质含沙量;i为数据编号;N 为数据总数。

从表2-6可见，对于Einstein 和Chien的数据，计算和实测床沙质含沙量的平均几何方差和均方根分别从2.34 和16580 减小到1.66 和12810，对Samaga等的数据则从1.52和2403分别降到1.14 和1108。在所有偏差比范围内，计算结果都有改进，以0.5～2.0的范围为例，对于Einstein和Chien的数据，从50.0% 提高到72.7%，对Samaga等的数据则从90.9%提高到了100.0%。

对于表2-7所示河流数据，计算结果也得到提高。所有河流数据的平均几何方差和均方根分别从2.03和568减小到1.78和492，在0.5～2.0范围内的偏差比则从56.0%提高到了67.4%。

图2-12和图2-13是这些结果的图示比较。图2-12显示了采用Kd修正对水槽试验资料的改进，图2-13则显示了对天然河流资料的改进。对美国运河数据的改进程度高于其他河流数据的改进;而对Atchafalaya河和Mississippi河的改进相对较小，部分归因于这两条大河的σg值较小，此外，对这两条大河的进一步改进需要考虑其他参数。

图2-14显示了相对中值粒径D50t/D50随床沙几何标准差σg的变化。图中共有335个数据点，包括Einstein (1978)、Einstein 和Chien (1953)、Guy等(1966)的水槽资料，位于Nebraska 州Cody 的Niobrara 河 (Colby& Hembree，1955)、位于Nebraska 州Dunning的Loup河中游 (Hubbell& Matejka，1959)的野外资料。资料限制在沙粒范围，其统计结果见表2-5，中值粒径为0.104～1.039mm，几何标准差为1.245～2.968，流量为0.019～16.06m3/s，流速为0.22～1.90m/s，水深为0.058～0.576m，能坡为0.00023～0.0193。

pagenumber_ebook=84,pagenumber_book=68

图2-12　Engelund-Hansen公式用于水槽试验的计算结果与实测床沙质含沙量的对比

(a)基于D50;(b)采用Kd修正

pagenumber_ebook=84,pagenumber_book=68

图2-13　Engelund-Hansen公式用于天然河流的计算结果与实测床沙质含沙量的对比

(a)基于D50;(b)采用Kd修正

图2-14中没有包括那些采用间接方法获得的漏测部分粒径分布的资料。众所周知，在天然河流的输沙率测验中存在底部泥沙的漏测问题。为了得到全沙输沙率，通常不得不采用一些非直接的方法来估算漏测部分的输沙率，如修正Einstein公式 (Modified Einstein Procedure)，这样得到的输移泥沙的粒径分布资料，不可避免地会有一定的误差。为了保证资料的可靠性和精度，在选用天然河流资料时，不包括那些含有用非直接测量方法来估算漏测部分泥沙的资料。美国Niobrara河的输沙率测验是在一个特别的收缩断面进行的，而美国Loup河中游的泥沙测验，则是在一个专门埋设于河底的紊动水槽中开展的。这两条河流泥沙测验的共同特点是不包含任何底部漏测泥沙，所有的输移泥沙都是直接的实测结果，相应的输移泥沙粒径分布资料也是可靠的。

由图2-14可见，D50t小于D50，并且D50t/D50随σg的增加而减小。原因是混合沙中较小的粒径更容易由水流挟带，即通常所说的水力分选作用。图2-14中还绘出了式 (2-48)的曲线，可以看到实测数据与公式计算结果接近。

pagenumber_ebook=85,pagenumber_book=69

图2-14　相对直径D50t/D50与几何标准偏差σg的关系

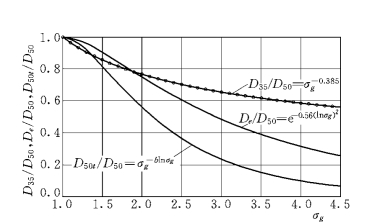
pagenumber_ebook=85,pagenumber_book=69

图2-15　D35/D50、De/D50和D50t/D50随σg的变化

图2-15绘出了相对粒径D35/D50、De/D50和D50t/D50随σg的变化。在σg=1.38时，D35/D50与D50t/D50相等;在σg=1.9时，D35/D50与De/D50相等。D35和D50t的值均小于D50，因此用D35或D50t计算的输沙能力大于用D50给出的输沙能力，但D35作为代表粒径仅在σg为1.9左右时才是正确的，而D50t始终小于可变代表粒径De。

本节所提出的粒径分布修正因子Kd，适用于非均匀沙条件下的床沙质输沙能力计算。以1965年4月16日Tarbert-Landing处的Mississippi河数据为例(Q=24470m3/s，W=1130m，h=14.42m，J=0.0000365，T=15.0℃，D35=0.167mm，D50=0.199mm，σg=1.648，Ct=136ppm，D50t=0.107mm (据悬移质输沙率资料计算))，具体的计算步骤如下:

第一步:以中值粒径D50作为床沙的代表粒径计算输沙能力。从上面所给数据出发，应用Engelund-Hansen公式计算的床沙质含沙量为Ctc=100.7ppm;

第二步:计算Kd，并修正上述计算结果。由式 (2-44)得到Kd=e0.5(1.2ln1.648)2=1.20，由此得到床沙质含沙量Ctc=1.20×100.7=120.5ppm;

第三步:计算D35、De和D50t。由式(2-55)、式(2-54)和式 (2-48)分别计算这三个特征粒径，结果为D35=0.164mm、De=0.171mm、D50t=0.147mm;

第四步:比较计算结果与实测资料的吻合程度。修正后的床沙质含沙量为120.5ppm，与Engelund-Hansen公式给出的100.7ppm 相比，更接近于实测值136ppm。并且床沙可变代表粒径De=0.171，小于实测的床沙D50=0.199mm。计算得到的D50t=0.147mm 则比实测值偏大，这可能是因为D50t=0.107mm 仅是实测悬移质部分的结果。

修正因子检验的优化方法

相关推荐