床沙粒径的对数正态分布探究

2025-09-29 理论教育版权反馈

【摘要】：如果通过对数变换，粒径分布可转换为对称的近似正态分布，则这种粒径分布叫做对数正态分布。图2-8和图2-9所示的床沙粒径分布可以由式或式表示的对数正态分布的累积分布函数描述，上式所表示的对数正态分布属于偏态分布，参数μy和σy确定了其分布特性。上式是均值为零、标准差为1的正态分布。

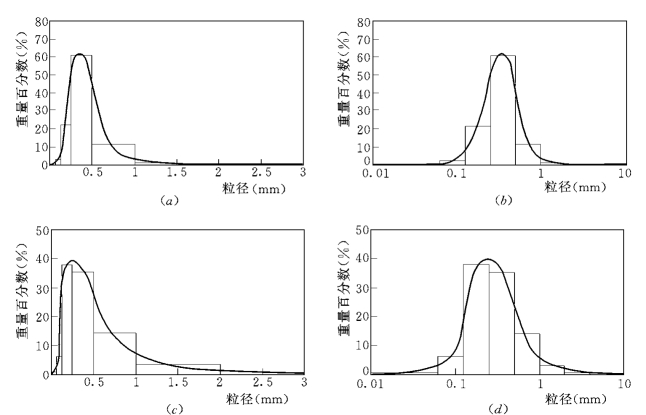
pagenumber_ebook=76,pagenumber_book=60

图2-8　位于New Mexico州Bernalillo附近的Rio Grande河的床沙粒径分布柱状图

(a)和(b)为2025年6月1日观测资料，D50=0.33mm，σg=1.62;(c)和(d)为2025年6月18日观测资料，D50=0.25mm，σg=1.4

床沙粒径的分布通常是偏态的 (Mahmood，1973a，b)。如果通过对数变换，粒径分布可转换为对称的近似正态分布，则这种粒径分布叫做对数正态分布。图2-8中给出了两个对数正态分布的例子，图中资料为位于New Mexico州Bernalillo附近的Rio Grande河的实测级配 (Nordin & Beverage，1965)。图2-8 (a)和2-8 (c)中的粒径分布曲线显然是偏态的。但当粒径采用对数尺度时，便得到了图2-8 (b)和2 8 (d)所示的对数正态分布曲线。图2 9给出了Rio Grande河大量实测床沙资料的对数概率图，可以看到，从10%～90%之间的泥沙十分接近对数正态分布，这种类型的对数正态分布在冲积河流的沙质河床中经常遇到。

考虑变量x 和y，它们之间的关系为y=ln(x)，x 的变化范围为0＜x＜∞，变量y 的平均值和标准方差分别为μy 和σy。如果y 服从如下高斯分布:

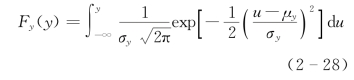
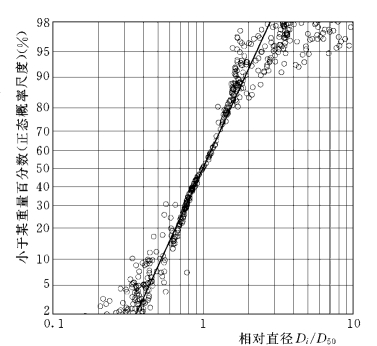
pagenumber_ebook=76,pagenumber_book=60

图2-9　床沙粒径分布图 (位于New Mexico州Albuquerque和Bernalillo附近的Rio Grande河，包括1952～2025年的实测沙样112组，D50=0.18～0.43mm，σg=1.36～2.78，实际粒径按σg=1.8标准化)

则变量x 服从如下对数正态分布:

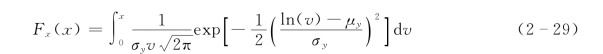
pagenumber_ebook=77,pagenumber_book=61

式中:u 和v 为积分变量。(https://www.chuimin.cn)

图2-8和图2-9所示的床沙粒径分布可以由式(2-28)或式(2-29)表示的对数正态分布的累积分布函数描述，上式所表示的对数正态分布属于偏态分布，参数μy和σy确定了其分布特性。对于非均匀的床沙来说，其颗粒级配一般都服从对数正态分布规律，通常用中值粒径D50和几何标准方差σg来描述。对于由D50和σg两个参数所确定的对数正态分布曲线，D50和σg与μy和σy的关系可以表示为: