大河流输沙能力公式

2023-06-22 理论教育版权反馈

【摘要】：Einstein 认为，水流的输沙能力与水流克服沙粒阻力所要求的能坡J′有关，而不是总能坡J。式表示的关系式与Velikanov、张瑞瑾、窦国仁分别提出的式 (2-2)、式(2-4)、式(2-5)表示输沙能力关系的形式基本相同。因此，在大河流的输沙能力计算公式中，选择合适的阻力公式，将比降表示为速度和水深的函数，是一种较为有效的处理办法。根据表2-1给出的414组大河流输沙资料点绘了Ct与Ψ 的关系，见图2-4。

Einstein (1950)认为，水流的输沙能力与水流克服沙粒阻力所要求的能坡J′有关，而不是总能坡J。将式(2-11)中的J 用J′代替，并考虑到泥沙在水中的相对容重，则基于无量纲的单位水流功率的输沙能力公式可以表示为:

pagenumber_ebook=68,pagenumber_book=52

含沙量Ct与无量纲的单位水流功率参数UJ/ω50之间的关系已经得到了大量实验室资料和一些小河实测输沙资料的证实 (Yang，1973;Yang& Molinas，1982;Yang&Kong，1991;Yang等，1996)。在天然河流上，特别是比降较小的大河流上，水面比降的精确测量具有较大的不确定性，比降测量的误差较大。为了避免比降误差的影响，在实际应用中常用的办法是选择合适的流速公式替换式 (2-11)或式 (2-12)中的比降项。这种替换方法曾得到了Simons和Sentürk (1992)的极力推荐，他们认为，一方面是水面比降的精确测量困难，另一方面是流速及流速分布的测量简单，精度较高，若进一步考虑到能坡与流速之间的密切关系，利用流速替代比降也就是顺理成章的事了。一个简单的方法就是采用Darcy-Weisbach阻力公式替换式(2-12)中的能坡项，即:

式中:f′为相应于沙粒阻力的Darcy-Weisbach 阻力系数。将式 (2-13)代入式 (2-12)并简化得到:

阻力系数f′可以由通用对数流速分布公式得到 (Simons&Sentürk，1992)。对于宽浅河流，垂线平均流速可以表示为:

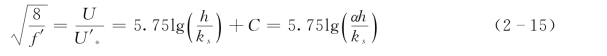
pagenumber_ebook=68,pagenumber_book=52

式中:C 和α 均为系数;ks为河床糙度;U′*为相应于沙粒阻力的摩阻流速。将式 (2-15)中关于f′的表达式代入式(2-14)，并用n D50替换ks，整理并简化后得到:

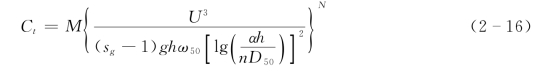
pagenumber_ebook=68,pagenumber_book=52

式中:n为系数。

由于lg(α/n)与lg(h/D50)相比要小得多，可以忽略不计，由此得到:

式中:Ψ 称为通用水流功率参数，具体表达式如下:

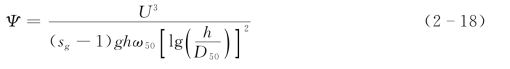
pagenumber_ebook=68,pagenumber_book=52

式(2-16)表示的关系式与Velikanov、张瑞瑾、窦国仁分别提出的式 (2-2)、式(2-4)、式(2-5)表示输沙能力关系的形式基本相同。但式 (2-2)、式 (2-4)、式(2-5)在进一步的处理中，将与水流的阻力有关的参数K、K1、K2均当作常数来处理，忽略了它们随水流条件的变化。虽然式(2-2)、式(2-4)、式(2-5)避免了直接使用比降作为独立变量，但采用忽略阻力影响的简单做法也是不可取的。

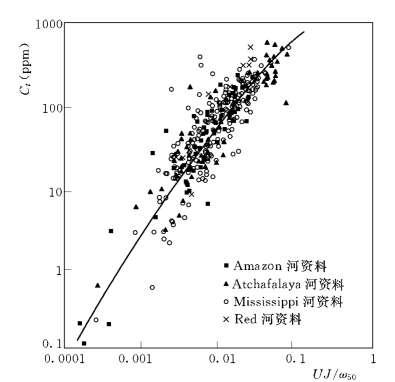
pagenumber_ebook=69,pagenumber_book=53

图2-4　实测床沙质含沙量与通用水流功率参数之间的关系

与本节观点不同，Yang 和Kong(1991)认为，采用阻力公式代替能坡的做法，由阻力公式转换带来的影响，可能远大于能坡测验误差对输沙能力计算精度的影响。这一说法对于那些完全忽略水流阻力影响的作法是有一定道理的。此外，当水面比降的测量精度较高时，比如控制条件较好的实验室水槽试验，也没有必要用流速项来替代比降项。在天然的大河中，水面比降往往极为平缓，比降J 的值在10-5数量级左右。对于比降如此小的河流，实际比降值对于野外测量中的任何微小误差都很敏感。因此，在大河流的输沙能力计算公式中，选择合适的阻力公式，将比降表示为速度和水深的函数，是一种较为有效的处理办法。

根据表2-1给出的414组大河流输沙资料点绘了Ct与Ψ 的关系，见图2-4。可以看到，Ct与Ψ 的关系较为密切。由于式(2-17)中的系数M 和指数N 都不是常数，所以Ct和Ψ 之间表现为非线性的关系。依据图2-4的资料，通过非线性回归得到如下适合于大河流的输沙能力公式(Molinas& Wu，2001):

式中:Ψ 的定义由式(2-18)给出;泥沙沉速的计算采用鲁比方法(Rubey，1933)。

大河流输沙能力公式

相关推荐