对推移质颗粒运动的紊动特性进行统计分析,探讨粒径、比重及水力比降对推移质紊动速度的影响,并定性总结推移层内平均紊动特性的变化规律。......
2023-06-22
1.3.3.1 水流条件的影响
1.紊动强度
各种水流条件下的颗粒三个方向的紊动强度及紊动能量沿垂线的分布见图1-52。从图中可以看出,纵向脉动速度的紊动强度随水深的增加而略有衰减,到接近水面时则减少明显。垂向和横向的紊动强度沿垂线的分布为中部流区稍大,底部流区和接近水面时偏小,在y/hm=0.25左右达到最大值。从数值上看,纵向脉动速度的紊动强度最大,垂向的紊动强度最小。
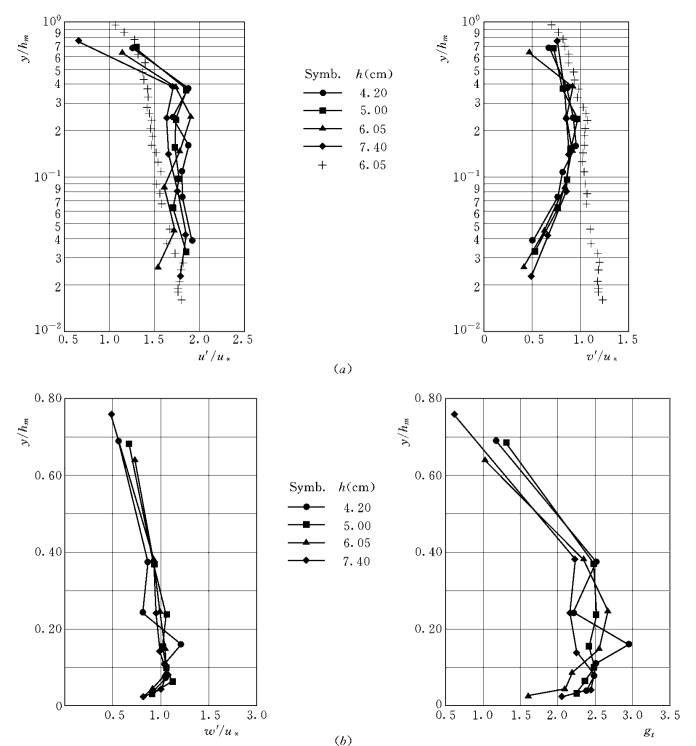
图1-52 颗粒脉动速度的紊动强度和紊动能量分布
图1-52中还画出了清水纵向和垂向紊动强度沿垂线的分布,在近底流区 (y/hm<0.1,大致以推移质运动为主)的颗粒纵向紊动强度与清水紊动强度接近,而垂向的紊动强度则明显偏小,说明在近底流区水流的紊动对颗粒的纵向脉动有重要影响,但颗粒因受空间尺度的限制而使其垂向紊动减弱。在中部主流区,颗粒的纵向紊动强度比清水的紊动强度大,垂向的紊动强度则与清水的紊动强度大致接近,说明在主流区,颗粒具有较大的惯性作用。在上部流区则因水流的紊动减弱而使颗粒的紊动强度明显减小。
如类比于水流的情况,定义颗粒的扩散系数为:
![]()
式中:l为颗粒与流体比拟的掺混长度。
由图1-52可知,就平均值而言有:
![]()
三个方向颗粒的扩散系数(εx、εy和εz)的大小应有如下关系:
![]()
根据试验条件可以推论,颗粒的扩散系数与流动的尺度有关,沿水深方向最小,沿水槽宽度方向次之,沿水流长度方向最大。
颗粒运动的紊动能量定义为:
![]()
其沿垂线的分布见图1-52,随离床面的距离而迅速增加,在y/hm=0.2~0.4之间达到最大值,再往上则逐渐减小。
图1-53 和图1-54分别为颗粒三个方向的紊动强度及紊动能量的垂线平均值随Re和Fr 的变化。颗粒的紊动强度随水流Re加大而减小的结果说明水流重力对减小颗粒紊动有重要作用。因水流的粘度不变,4组试验的平均流速变化不大,即水流的惯性力大致相当,则水深(重力)越大,抑制紊动的能力越强,相应地使颗粒的紊动强度减弱。从图1-54可以看出,各变量都随Fr的增加而加大。Fr表示水流的惯性力与重力之比,当水流的惯性力变化不大时,图1-54的结果同样表明颗粒的紊动随水流重力的减小 (Fr加大)而加大。
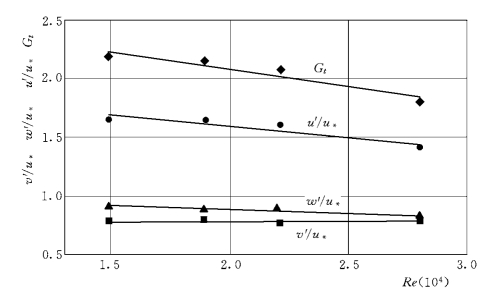
图1-53 紊动参数随Re的变化
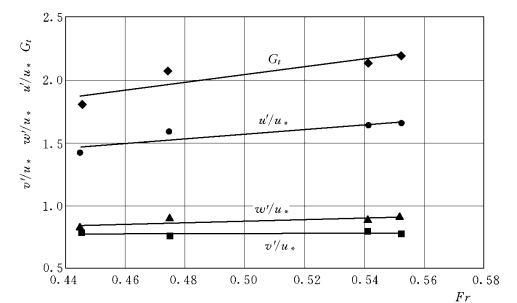
图1-54 紊动参数随Fr的变化
2.颗粒的紊动剪切应力及能量损耗
如定义颗粒的剪切应力为:
![]()
τp沿垂线的分布见图1-55,其绝对值比清水水流的紊动剪切应力小,将图1-55中的直线延长到床面时:
![]()
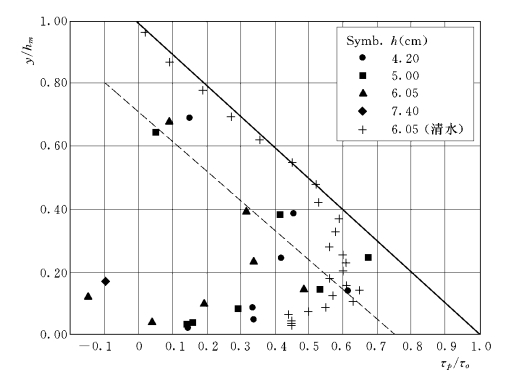
图1-55 颗粒剪切力分布
即按式(1-61)定义的颗粒剪切应力在接近床面时约为水流紊动剪切应力的75%。
定义颗粒因克服当地阻力而损失的能量为:
![]()
根据实测资料计算的结果见图1-56。其沿垂线的分布可用下式表示:

图中“+”为h=6.05cm 组次的清水水流因克服当地阻力而损失能量的分布。从图1-56可以看出,在y/hm>0.2的流区随高度的增加而大致线性减小,当y/hm<0.2时,e随高度的减小而迅速增加,因克服当地阻力而损失的能量主要集中在y/hm<0.2的流区。
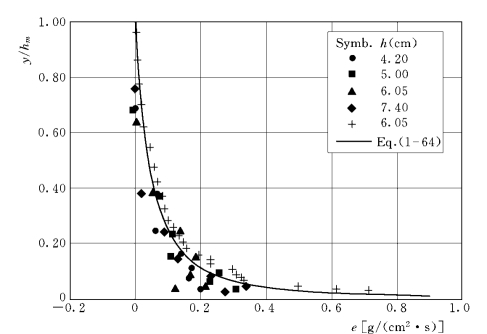
图1-56 颗粒因克服当地阻力而损失的能量
1.3.3.2 粒径的影响
1.紊动强度的变化
实测的紊动强度资料见表1-23,图1-57为颗粒三个方向脉动速度的紊动强度及紊动能量沿垂线的分布。从图中可以看出,在y/hm小于0.25的下部流区,颗粒纵向速度的紊动强度变化不大,在y/hm大于0.25的上部流区则随高度的增加而变小。颗粒垂向和横向流速的紊动强度以及紊动能量沿垂线的分布在中部流区稍大,底部流区和接近水面时偏小,在y/hm=0.25左右达到最大值。从数值上看,颗粒的纵向紊动强度最大,垂向最小,4组资料平均值的比例大致为:u′/v′=2.33,u′/w′=1.91,v′/w′=0.822,即u′>w′>v′。颗粒纵向速度的紊动强度与对应清水的紊动强度差别不大,垂向紊动强度则小于清水。
表1-23 紊动参数统计表
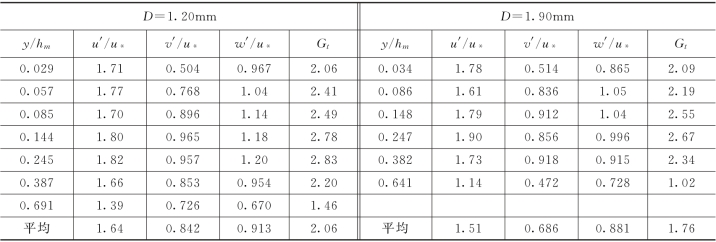
续表
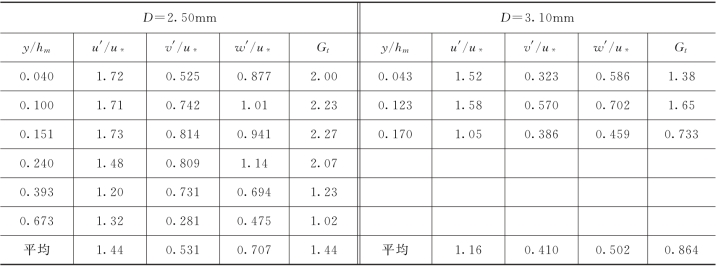
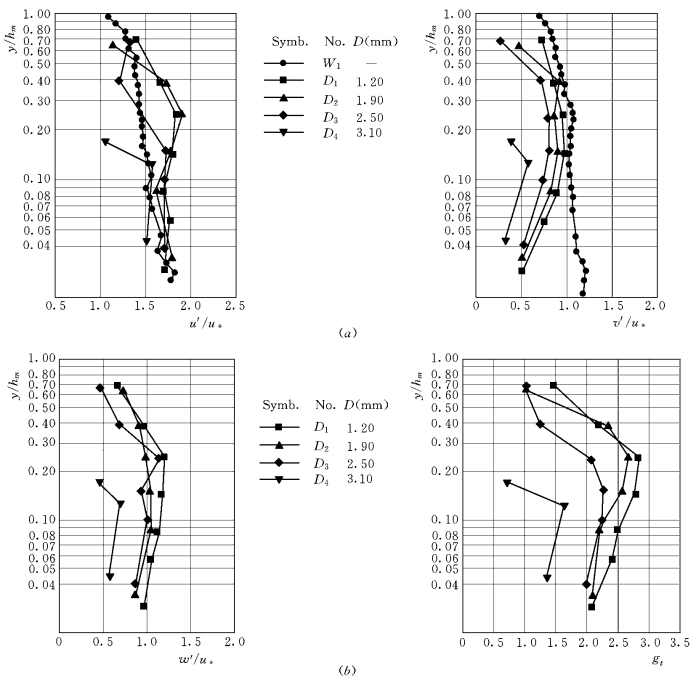
图1-57 颗粒脉动速度的紊动强度分布
图1-58为总体样本的紊动强度u′与颗粒速度空间变化和时间变化共同产生的紊动强度u′t的对比,两者基本一致,说明颗粒速度的紊动强度是由速度的空间变化 (欧拉场)和时间变化(拉格朗日场)共同作用的结果。
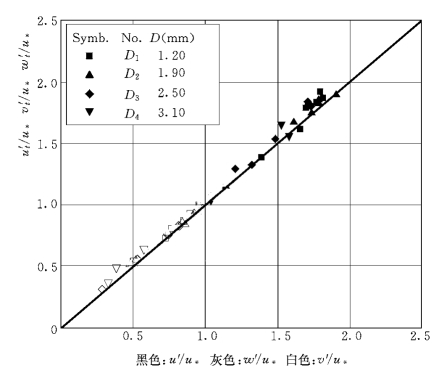
图1-58 两种算法的紊动强度对比
图1-59为颗粒三个方向的紊动强度及紊动能量的垂线平均值随粒径的变化,它们均随粒径的加大而减小。假定尺度比颗粒小的旋涡对颗粒的脉动没有影响,则颗粒越大,对其紊动起作用的旋涡的分界尺度也越大,其总的紊动能量也随之减小。

图1-59 紊动强度随粒径的变化
2.颗粒的紊动应力及能量损失
根据式(1-61)计算的以悬移质运动为主的前三组试验的颗粒紊动剪切应力沿垂线的分布见图1-60 (a),图中的虚线代表流场中总剪切应力的线性分布。在上部流区,清水的紊动应力接近流体的总应力,在下部流区逐渐减小。在y>0.2hm的上部流区,颗粒的紊动应力亦接近直线分布,但数值约为清水紊动应力的75%。在y<0.2hm的底部流区,颗粒的紊动应力逐渐减小,与清水紊动应力的变化趋势一致。

图1-60 紊动应力和能量损失率沿垂线的分布
颗粒因克服当地阻力的能量损失率e沿垂线的分布见图1-60 (b),清水和颗粒的能量损失率基本接近。在y>0.2hm的上部流区,e值往上线性减小,当y<0.2hm后,e值随接近床面的距离而迅速增加,其沿垂线的分布亦可用式(1-64)表示。
试验结果表明,不同水流条件、不同粒径的紊动应力和能量损失率的变化规律是一致的。
3.概率密度的变化
在进行脉动速度的概率密度分布的分析中,将流场分成近壁流区y/hm<0.1 和上部流区y/hm≥0.1。概率密度的三阶矩为偏态系数Cs,四阶矩为峰态系数Ce,正态分布的Cs=0,Ce=3.0。各统计参数见表1-24。
表1-24 脉动速度概率密度分布参数
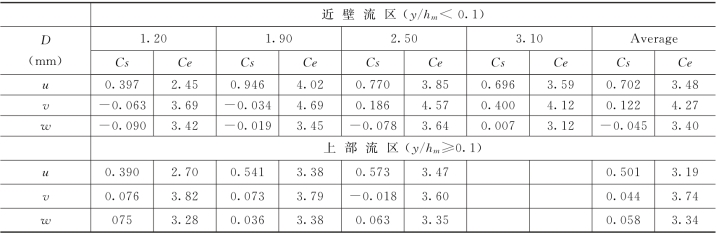
图1-61为颗粒纵向脉动速度的概率密度分布,图中还画出了正态分布曲线以做对比。在近壁流区,各种粒径的纵向脉动流速u/u′的概率密度分布基本一致,平均偏态系数Cs=0.702,中值负偏,长尾在正轴一侧,表明较大纵向速度的比例较大。峰态系数Ce=3.48,大于正态分布的3.0,即概率密度分布相对尖痩,脉动速度分布相对集中。概率密度分布的偏态特性表明,在近壁流区的纵向脉动流速将受到空间条件的约束。上部流区纵向脉动流速u/u′仍存在负偏,Cs=0.501,峰态系数则接近于正态分布的3.0。
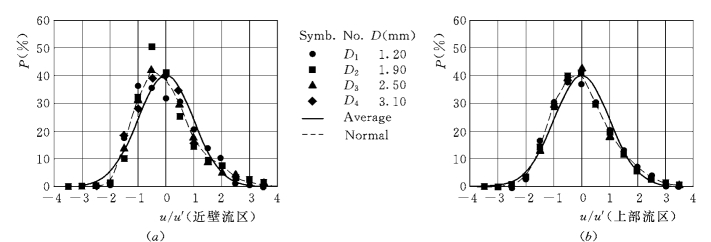
图1-61 纵向脉动速度的概率密度
图1-62为垂向脉动流速v/v′的概率密度分布,近壁流区的偏态系数较小,图形基本对称。由于受到空间尺度的制约,概率密度分布尖痩,表明瞬时速度在垂向上的波动相对较小。上部流区已接近正态分布,即颗粒的运动受边界约束的影响减小,更接近于各向同性的紊动。
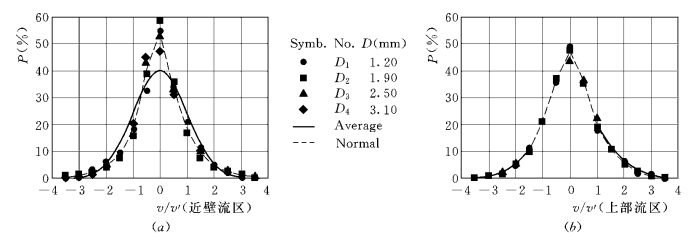
图1-62 垂向脉动速度的概率密度
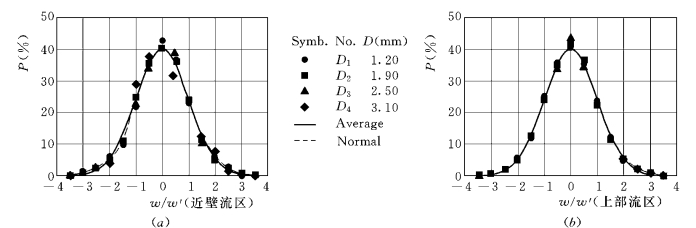
图1-63 横向脉动速度的概率密度
图1-63为横向脉动流速w/w′的概率密度分布,近壁流区和上部流区的图形都基本对称分布,由于在水槽的中线附近量测,颗粒在横向上的运动不受约束,概率密度近似为正态分布。
从上述结果的对比可以看出,粒径对概率密度的分布没有明显的影响,即在本试验的条件下,各种粒径颗粒运动的脉动特性是相似的。
(本章作者:王兴奎)
有关泥沙研究进展的文章

为统计颗粒运动的各种参数,将实测资料沿垂线分区。表1-19实测颗粒速度和浓度的平均值图1-45中Uw为对应组次的清水流速,同时给出了对数区的回归直线。图1-45中近底两个点为推移层内颗粒的平均运动速度。颗粒平均速度与相应清水平均速度的比值的平均值为0.826,说明颗粒的平均速度小于清水。......
2023-06-22

采用三维粒子示踪测速技术,通过分别改变示踪粒子的粒径、比重以及水力比降等条件,观测了10种不同水沙条件下推移质颗粒的三维运动。对推移质颗粒的平均运动规律进行统计分析,探讨粒径、比重及水力比降对推移质运动速度的影响,并分别根据Einstein和Bagnold的研究方法从实测资料得出推移质纵向平均速度的表达式。由图1-12可知,随着坡降的增加,推移质颗粒的速度明显增大,颗粒与水流的相对运动速度减小。......
2023-06-22

分析具有代表性的6组试验的推移质颗粒的单步运动,对大量粒子的运动规律进行统计分析。图1-34典型跃移轨迹xz平面图1-33、图1-34中L 为粒子跃移的单步步长,L1为颗粒起跃至达到最高点的长度,H 为跃高,d 是颗粒单步运动横向摆动幅度,uo、vo、wo分别为起跃点的纵向、垂向和横向速度,ue、ve、we则为降落点的纵向、垂向和横向速度。......
2023-06-22

全动床复式河槽由两个对称的滩地及主槽组成,水槽长50m,宽度6m,深1m,由中值粒径为0.8mm 的天然沙均匀构筑而成。图9-20全动床复式河槽初始断面形态全动床复式河槽水槽试验研究:河道完全粗化后能量损失、阻力系数沿程变化,推移质输沙率的变化特性,床沙中值粒径的横向变化与沿程变化等。这种趋势可以表达为图9-21不同坡度的沿程变化归槽水流;漫滩水流图9-23为清水作用下全动床复式河槽输沙率随时间的变化关系图。......
2023-06-22

运动素质包括耐力、力量、爆发力、速度、柔韧等,是完成专项动作的保证。运动素质具有专项特征,是专项动商的机能保障。足球运动员身体素质必然要适应于足球的运动需求和特征,运动素质不是一成不变的,而是存在高低起伏,这就导致动商产生波动。力量是足球动商的动力之源。运动素质逐渐不再是决定一个足球队最关键的成败因素,依靠几个队员打球的现象会越来越少。......
2023-10-23

所谓电弧的稳态,是指电弧长度、电弧电压和电流在较长时间内不改变数值,处在相对稳定的状态。因此,就要求弧焊电源在焊接中,当电弧长度、电弧电压和电流变化时,必须具有满足动态电弧负载要求的特性,该特性就是弧焊电源的动特性。弧焊电源的动特性对电弧焊中的引弧、燃弧和熔滴过渡状态具有重要的影响,它是能否获得满意焊缝质量的重要因素之一。......
2023-06-30
相关推荐