采用三维粒子示踪测速技术，通过分别改变示踪粒子的粒径、比重以及水力比降等条件，观测了10种不同水沙条件下推移质颗粒的三维运动。对推移质颗粒的平均运动规律进行统计分析，探讨粒径、比重及水力比降对推移质运动速度的影响，并分别根据Einstein和Bagnold的研究方法从实测资料得出推移质纵向平均速度的表达式。由图1-12可知，随着坡降的增加，推移质颗粒的速度明显增大，颗粒与水流的相对运动速度减小。......
2023-06-22
颗粒三维运动的平均特性分析
【摘要】：为统计颗粒运动的各种参数，将实测资料沿垂线分区。表1-19实测颗粒速度和浓度的平均值图1-45中Uw为对应组次的清水流速，同时给出了对数区的回归直线。图1-45中近底两个点为推移层内颗粒的平均运动速度。颗粒平均速度与相应清水平均速度的比值的平均值为0.826，说明颗粒的平均速度小于清水。
1.3.2.1 水流条件的影响
在4种水深条件下进行试验，研究不同水流条件对粗颗粒运动规律的影响。用二维激光流速仪测量观测断面中垂线上的流速。选用粒径D=1.90mm、比重为1.05的均匀轻质塑料圆球做示踪颗粒，其静水沉速用Rubey(1933)公式计算:
计算得出ω=2.20cm/s。
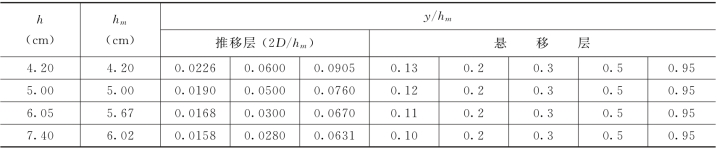
为统计颗粒运动的各种参数，将实测资料沿垂线分区。当y≤2D 时为推移层，将其分为2个区，对y＞2D 的悬移层分5个区，分区结果见表1-17。将实测的单颗粒的速度按相对高度分区，分别计算各区的统计特征值。颗粒的浓度定义为每一区间的平均颗粒数，根据实测的颗粒浓度分布可以算出Rouse方程的悬浮指数Z1。
表1-17 颗粒平均速度统计分区
1.平均速度的变化规律
每组试验先进行清水流场的量测，然后在相同的水流条件下进行颗粒运动的试验，清水和颗粒试验的基本参数见表1-18。
表1-18 试验参数表
式中:Ua为离床面高度y 处的颗粒平均速度;κ为卡门常数;B 为积分常数。
表1-19 实测颗粒速度和浓度的平均值
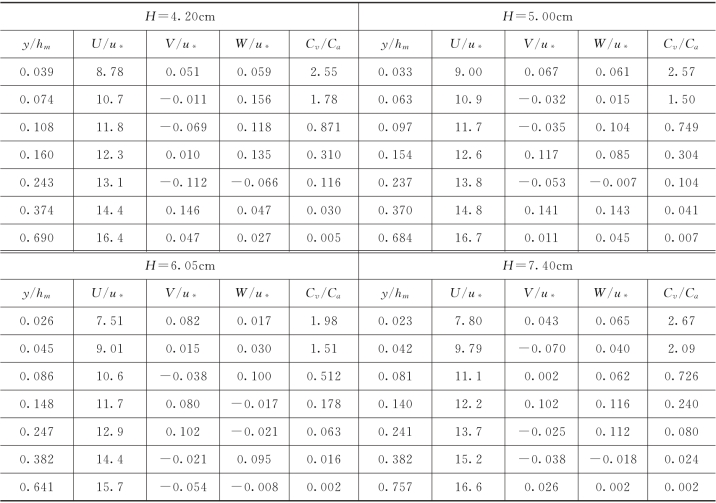
图1-45中Uw为对应组次的清水流速，同时给出了对数区的回归直线。图1-45左上图还给出了Nezu和Rodi(1986)的一组试验资料，可以看出，试验的清水流速分布与Nezu的结果完全一致，说明二维激光流速仪的测量结果是可靠的。图1-45中近底两个点为推移层内颗粒的平均运动速度。用式(1-55)对悬移质运动区域的实测资料进行回归计算得出:各组试验的κ值变化不大，平均为0.393，说明颗粒纵向平均速度沿垂线的分布遵循对数规律，积分常数B 的平均值为17.2。颗粒平均速度与相应清水平均速度的比值的平均值为0.826，说明颗粒的平均速度小于清水。
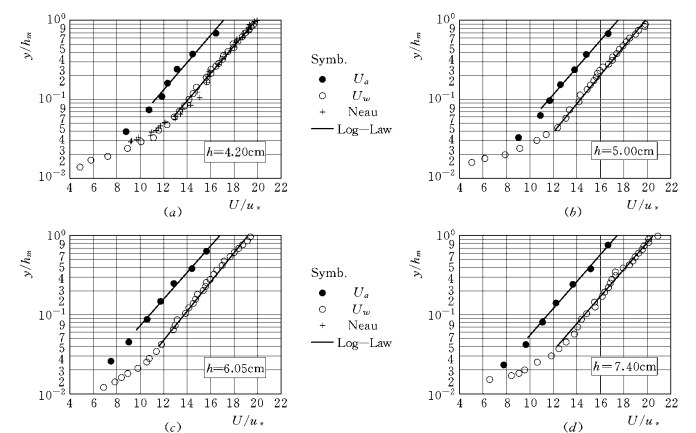
图1-45 纵向平均速度分布
图1-46为垂向和横向平均速度沿垂线的分布。两个方向平均流速的绝对值均小于0.3cm/s，属于量测误差的范畴，即垂向和横向没有明显的时均流动，完全是随机的脉动。
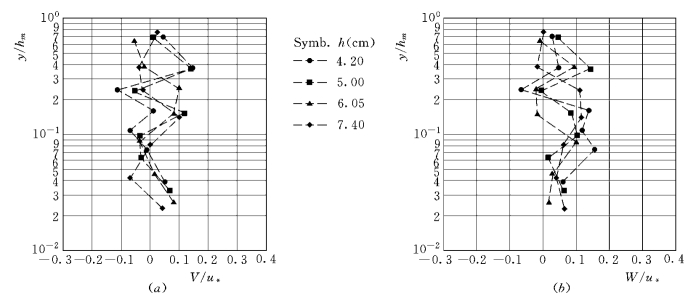
图1-46 垂向和横向平均速度分布
2.平均浓度的垂线分布
对颗粒浓度的垂线分布，邵学军和夏震寰(1990)从泥沙颗粒的随机运动出发进行了理论分析。基于颗粒位移速度的微分方程，推导得出颗粒转移概率密度P′，其物理意义是颗粒于时刻to在点yo投放入紊动流场以后，于时刻t在y 处出现的概率密度。设在时刻to从点yo处同时投放N 个颗粒，到t时刻在y 处有NP个颗粒。如颗粒的密度相同，大小均匀，则NP与颗粒的体积浓度成正比。假定在观测点上游投放的颗粒到达观测区域时在垂线上的位置已处于稳定的随机分布，则可定义颗粒在某一高程出现的概率为颗粒在该位置的浓度，如在某一区间的颗粒数除以该区的高度即为这一区间的平均颗粒浓度。采用Rouse公式对悬浮区的颗粒浓度(图中双对数直线的范围)进行回归:
取推移质与悬移质交界面 (y=2D)上的浓度为Rouse方程中的参考浓度Cva(该数值使y=2D 时Cv=1)，可以算出各点的相对浓度，进而得出颗粒沿垂线的浓度分布。
图1-47为颗粒浓度沿垂线的分布，图中参考浓度的高度取a=2D，此处的Cv/Ca=1。对悬浮区的颗粒浓度进行回归计算，可以得出Rouse公式的悬浮指数Z1，结果见表1-18。实测的悬浮指数Z1小于理论值Z，修正系数β的平均值为1.50，与Vanoni(1946)的研究结果一致。
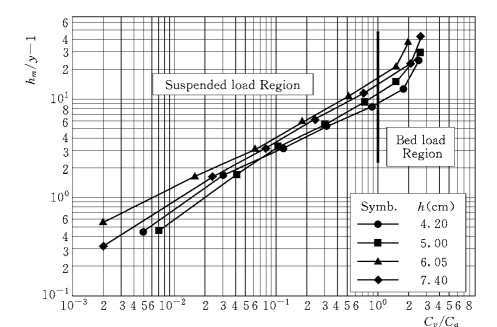
图1-47 平均浓度分布
1.3.2.2 粒径的影响
水流为恒定均匀流，保持水流条件不变，水流能坡Je=0.000868，水深h=6.05cm，垂线平均流速Uw=0.371m/s。当b/h=4.88 时，hm=0.938h=5.67cm。摩阻流速u*=
选用4种不同粒径 (D=1.20、1.90、2.50、3.10mm)、比重为1.05的均匀轻质塑料圆球做示踪颗粒，组次编号为D1～D4，相应的水流试验编号为W1。在量测断面上游4.0m 左右的水面中线按一定的时间间隔放入粒径相同的单个颗粒，颗粒到测量断面时已达到稳定的随机运动状态。当颗粒穿过镜头的测量区时，记录下颗粒的三维运动轨迹，经过校正后即可得出单个颗粒连续运动轨迹的坐标，根据采样频率可以求出三个方向速度的序列值。试验基本参数见表1-20。
从表1-20的资料可知，对前三组以悬移质运动为主的资料，计算的颗粒悬浮指数Z=1.75～2.99。第四组的Z 值较大，颗粒主要以推移质的形式运动。按Einstein的定义，推移层的厚度为2D，图1-48为各组试验推移层内颗粒运动的平均轨迹，计算时先将每个颗粒的起点平移到离床面一个颗粒的高度再进行平均。
表1-20 试验参数表
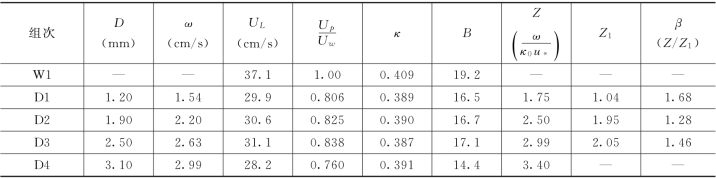
图1-48 推移层内颗粒的平均运动轨迹
从图中的曲线可以看出，当D≤2.50mm 时，近壁处颗粒的平均运动轨迹沿程抬升，即颗粒有离开底部进入主流区的运动趋势，将主要以悬移质的方式运动。对D=3.10mm 的曲线，颗粒先是上升，在y＜2D 的高度内到达顶点，然后下降，表现出明显的推移质运动特性，即该组试验主要是推移质颗粒。实测资料也表明，该组试验的运动颗粒全部集中在y＜0.2h的范围内，且在y＜0.1h(≈2D)的流区内运动的颗粒占98%。根据试验结果，可以取Z=3做为推移质和悬移质的分界指标，这与Bagnold(1966)的研究结果一致。
1.平均速度的变化规律
将实测的颗粒速度沿垂线分区进行统计。根据前面的分析，当y≤2D 时为推移层。当y＞2D 时为悬移层，根据各组试验实测点数的多少分成不同的区，实际分区的结果见表1-21。
表1-21 颗粒平均速度统计分区
表1-22为实测的颗粒时均速度的分区统计值，将颗粒起始点的坐标位于某一流区的点均作为该区的资料进行平均，得出该流区的代表高度和平均速度。
表1-22 实测颗粒平均速度
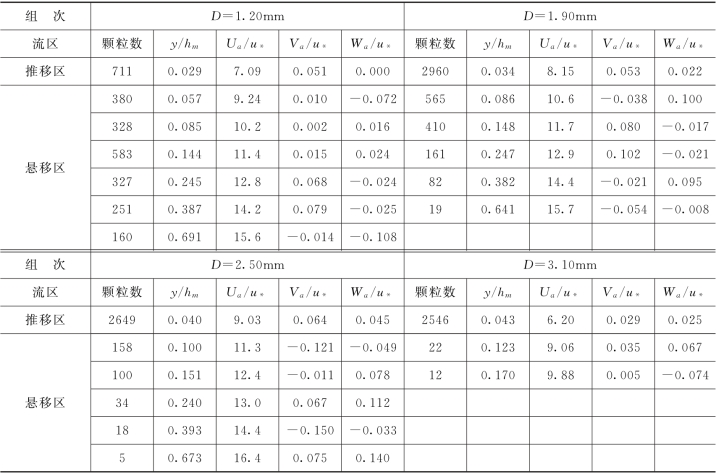
图1-49为颗粒纵向平均速度的垂线分布，图中近底第一点为推移层内颗粒的平均速度。各组试验的κ值变化不大，平均为0.389，与明槽水流的卡门常数κ0值基本一致，说明颗粒纵向平均速度沿垂线的分布仍遵循对数规律。颗粒的运动速度低于清水水流，前3组与清水流速比值的平均值为0.823，第4组的平均流速明显偏小，说明这一组试验的颗粒主要以推移质的形式运动。
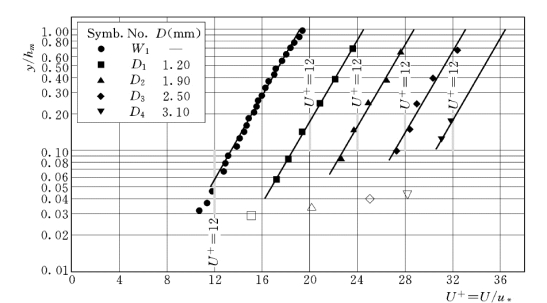
图1-49 纵向平均速度分布
图1-50为垂向和横向平均速度沿垂线的分布。两个方向的平均速度的绝对值一般都小于0.3cm/s，属于量测误差的范围，说明颗粒在垂向和横向上没有趋势性的平均运动，亦间接说明了试验系统处于稳定的状态。
图1-50 垂向和横向平均速度沿垂线的分布
2.平均浓度的变化规律
颗粒浓度由表1-22各区的颗粒数计算。图1-51为颗粒浓度沿垂线的分布，图中的参考浓度的高度取a=2D。图中的 “*”为y=2D 的位置，其上方为推移区，下方为悬移区。
图1-51 平均浓度分布
从图1-51可以看出，颗粒浓度的垂线分布与Rouse公式一致，从回归曲线可以求出实测资料的悬浮指数Z1，见表1-20。对以悬移运动为主的前3组试验，Z1小于理论值Z，修正系数β(=Z/Z1)的平均值为1.47，与Vanoni(1946)的研究结果是一致的。对第4组试验，因颗粒主要为推移质运动而没有可比性。
有关泥沙研究进展的文章
- 详细阅读
-
颗粒三维运动中的紊动特性分析详细阅读
在上部流区则因水流的紊动减弱而使颗粒的紊动强度明显减小。图1-56颗粒因克服当地阻力而损失的能量1.3.3.2粒径的影响1.紊动强度的变化实测的紊动强度资料见表1-23，图1-57为颗粒三个方向脉动速度的紊动强度及紊动能量沿垂线的分布。......
2023-06-22
- 详细阅读
-
推移质颗粒单步运动的统计规律分析详细阅读
分析具有代表性的6组试验的推移质颗粒的单步运动，对大量粒子的运动规律进行统计分析。图1-34典型跃移轨迹xz平面图1-33、图1-34中L 为粒子跃移的单步步长，L1为颗粒起跃至达到最高点的长度，H 为跃高，d 是颗粒单步运动横向摆动幅度，uo、vo、wo分别为起跃点的纵向、垂向和横向速度，ue、ve、we则为降落点的纵向、垂向和横向速度。......
2023-06-22
- 详细阅读
-
颗粒污泥的性质分析详细阅读
成熟的颗粒污泥，VSS/SS一般为7%～80%，但根据废水性质其范围可在30%～90%。一般来说，反应器沿高度的群落演替遵循9.3.5中所述规律，而单一颗粒污泥的生物构成遵循生物代谢规律，即产酸细菌主要在颗粒表面，产甲烷细菌主要在颗粒内部。......
2023-06-19
-
基于颗粒运动的Lagrange方程PDF模型详细阅读
与Boltzmann方程方法相对应的另一类动理学方法是基于颗粒运动Lagrange方程的PDF输运方程方法。这一节将基于颗粒运动的Lagrange方程，应用描述显著碰撞耗散颗粒系统的RET 理论 ，考虑碰撞颗粒之间的运动相关性，建立高含沙紊流型两相流的泥沙颗粒相本构关系式，并对流场梯度效应进行检验。......
2023-06-22
- 详细阅读
相关推荐