现有的三维测速多数是对水流结构及悬移质的测量，对推移质运动的观测则非常少见。对此Muste et al. 对毫米量级的粗颗粒泥沙运动进行了试验研究，所得的两相速度差在纵向和垂向上基本都与ω在同一量级。刘大有等将近壁颗粒的脉动划分为两种形式，即除了跟随水流的湍流脉动外，还存在颗粒跃移与壁面碰撞等方式引起的非湍流脉动。Muste et al. 对粗颗粒泥沙的观测也表明，近壁区流体的垂向脉动强度要小于颗粒脉动。......
2025-09-29
推移质颗粒单步运动的统计规律分析
【摘要】：分析具有代表性的6组试验的推移质颗粒的单步运动，对大量粒子的运动规律进行统计分析。图1-34典型跃移轨迹xz平面图1-33、图1-34中L 为粒子跃移的单步步长，L1为颗粒起跃至达到最高点的长度，H 为跃高，d 是颗粒单步运动横向摆动幅度，uo、vo、wo分别为起跃点的纵向、垂向和横向速度，ue、ve、we则为降落点的纵向、垂向和横向速度。
分析具有代表性的6组试验的推移质颗粒的单步运动，对大量粒子的运动规律进行统计分析。从试验结果来看，颗粒单步步长以及跳跃高度均随水流速度增大而增大，随颗粒粒径和比重增大而减小，较粗颗粒的单步运动距离并没有Einstein假定的100D 这么大。从统计规律来看，推移质单步步长的概率密度服从Γ 分布，颗粒起跃段步长与总步长之比接近一个常数。
1.2.5.1 基础资料
从表1-6中选取的6组资料的颗粒跃移运动的各统计参数见表1-10。
表1-10 颗粒跃移统计参数
在计算分析中，当颗粒在一步运动中的最高点离开床面超过1D 高度后，即认为其进行跃移运动，选取典型轨迹见图1-33和图1-34。
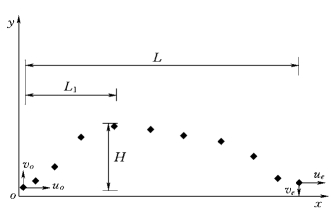
图1-33 典型跃移轨迹xy 平面
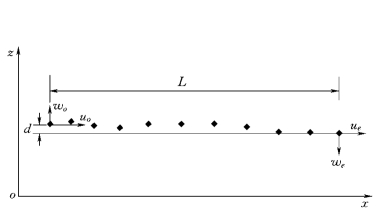
图1-34 典型跃移轨迹xz平面
图1-33、图1-34中L 为粒子跃移的单步步长，L1为颗粒起跃至达到最高点的长度(以后简称起跃段长)，H 为跃高，d 是颗粒单步运动横向摆动幅度，uo、vo、wo分别为起跃点的纵向、垂向和横向速度，ue、ve、we则为降落点的纵向、垂向和横向速度。定义起跃角η=arctg(vo/uo)、降落角φ=arctg(ve/ue)，可以描述粒子跃移和降落时在垂向上的运动幅度，定义颗粒横向摆动幅角δ=arctg(d/L)，用来描述颗粒在一次单步运动过程中的横向运动幅度。
表中各参数定义同前，带上划线的量为该量在一组试验中的平均值。实测资料表明:颗粒单步步长最小值在10D 以下，最大则超过100D，步长值与颗粒的本身性质及水流条件有关。根据表1-10的资料可知，步长随颗粒粒径和比重的增大而减小，随水流速度(比降)的增大而增大，颗粒的跃移高度与单步步长有相同的变化趋势。起跃角的变化范围是0.9°～24°，降落角则为0.4°～9.5°，从平均值来看，水流速度越快，起跃角和降落角越小;颗粒粒径和比重越大，颗粒跳跃的角度越小。从横向上的运动来看，颗粒在一次跳跃的过程中左右摆动的幅度最大不超过10D，平均值则基本接近于零，横向摆动幅角的计算结果也体现了同样的规律，说明颗粒跃移时横向上没有运动趋势。
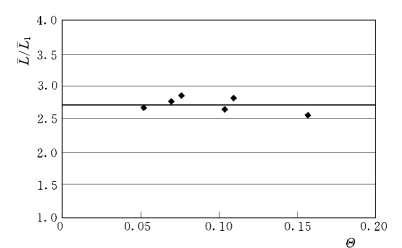
图1-35 
与Θ 的关系
颗粒起跃段长L1的平均值与平均步长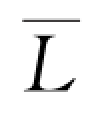
的比值基本不变，平均为0.368左右，也即L/L1=2.72，见图1-35，这与胡春宏的研究结果是一致的(L/L1=2.79)。
1.2.5.2 单步运动参数的概率密度分布
关于跃高和跃长究竟符合什么分布，从最初Einstein认为的单步距离符合定参数的指数分布，发展到目前普遍承认的Γ 分布，前人已经进行了比较多的讨论和研究。试验结果表明，颗粒单步步长及跃高的概率密度均服从Γ 分布，以粒径0.13cm 组的试验数据为例，图1-36和图1-37分别画出了跃长和跃高的概率密度分布拟合曲线。
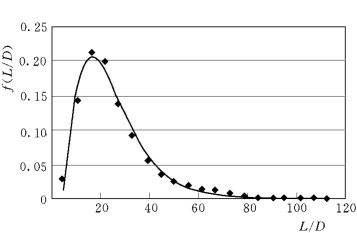
图1-36 颗粒跃长的概率分布
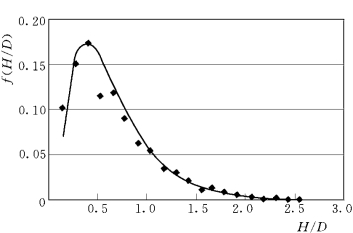
图1-37 颗粒跃高的概率分布
图1-36和图1-37中点据即为实测各区的概率密度，曲线则为拟合的Γ分布曲线:
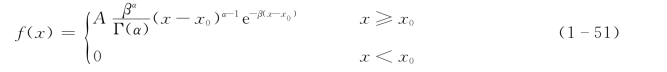
其中A 为调整系数，α和β 是分布参数，当α=1时为指数分布，x0为分布曲线的起点参数。
其他几组试验的统计规律基本相同，具体参数值见表1-11和表1-12。第六组试验由于水流作用力较大，所获得的典型跃移颗粒数较少，故不作分析。
表1-11 步长Γ分布的统计参数
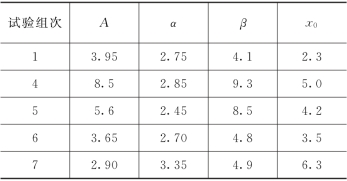
表1-12 跃高Γ分布的统计参数
为了使不同水流和泥沙条件下的实测资料能相互比较，采用相对步长L/L来对五组试验颗粒的单步运动距离进行统计，如图1-38所示。从图可见，相对步长的概率密度分布依然服从Γ 分布，并且不同粒径系列的三组试验数据基本重合，说明颗粒的相对步长的概率密度分布不受粒径的影响;但随比重的减小或水流速度的增大，概率密度分布的峰值变小，也即在轻质沙或高流速的条件下，颗粒的步长分布范围增大，说明颗粒的比重和水流速度对相对步长的概率密度分布有一定的影响。(https://www.chuimin.cn)
1.2.5.3 跃移速度的概率密度分布
颗粒单步跳跃过程中在起跃点和降落点处三个方向上的平均速度分量见表1-13。
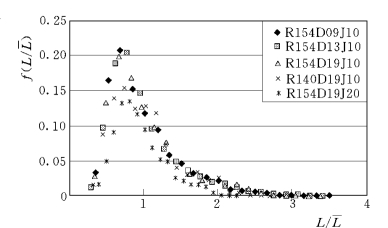
图1-38 相对步长的概率密度分布
表1-13 起跃速度和降落速度分量
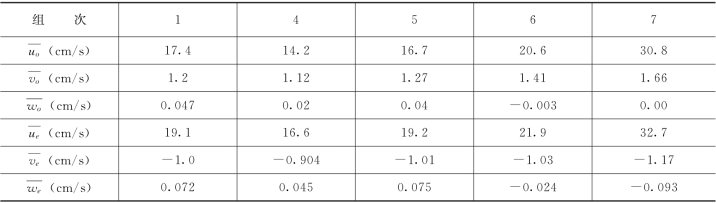
其中uo、 vo、 wo分 别代表颗粒起跃时在纵向、垂向和横向上速度分量的平均值，ue、ve和 we则是颗粒降落时的相应速度平均值。不难发现，颗粒在跃移运动过程中，在距离床面相同高度处，下落过程中的粒子纵向速度总大于上升阶段的速度;横向平均速度的绝对值维持在0.1cm/s以下，可以认为粒子在横向上没有趋势性的运动。
图1-39～图1-44别给出了五组试验中各速度分量的概率密度分布，由图1-39和图1-40可知，无论是相对起跃速度还是相对降落速度，在纵向上的概率密度均接近正态分布:
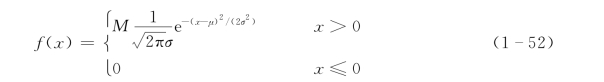
式中:M 为修正系数;μ 和σ 为分布参数，具体统计数值见表1-14。
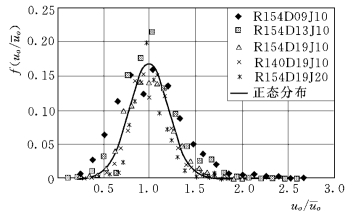
图1-39 纵向相对起跃速度的概率分布
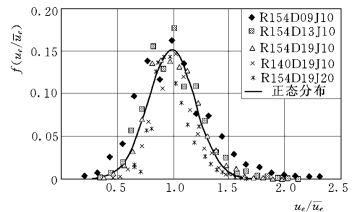
图1-40 纵向相对降落速度的概率分布
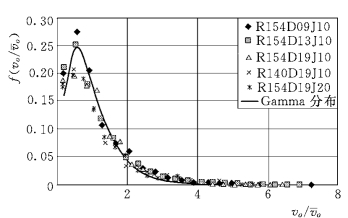
图1-41 垂向相对起跃速度的概率分布
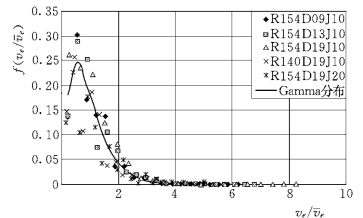
图1-42 垂向相对降落速度的概率分布
图1-43 横向起跃速度的概率分布
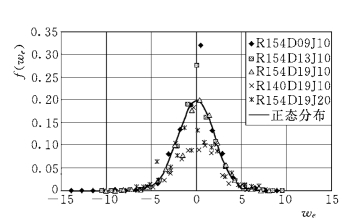
图1-44 横向降落速度的概率分布
表1-14 纵向相对速度概率密度分布参数
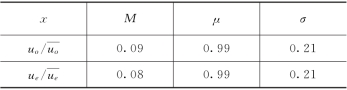
表1-15 垂向相对速度概率密度分布参数
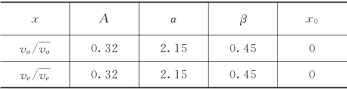
图1-41和图1-42表明，在垂向上，由于颗粒与床面之间的碰撞，起跃速度和降落速度出现低速运动的几率大大减小，统计的概率密度分布偏离了正态分布，而更倾向于Γ分布。根据式(1-51)，分布参数见表1-15。
表1-16 横向速度概率密度分布参数
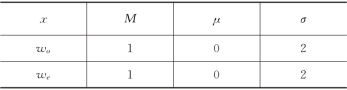
图1-43和图1-44进一步表明，横向上的颗粒运动并不受边壁的干扰，速度平均值很小，可以认为粒子只是随机摆动，各统计参数见表1-16。
相关文章
- 详细阅读
-
推导推移质公式详细阅读
推移质公式推求当运动泥沙与床面泥沙的交换达到平衡，即单位时间内自单位床面上冲刷外移的泥沙数量正好与沉积下来的泥沙数量保持相等时的输沙率。Einstein 经过推导得出在单位面积上将有重量为的泥沙被冲刷外移，其中A1、A2为与泥沙颗粒形状有关的系数。图1-2修正的Einstein公式与实测资料的对比图1-2修正的Einstein公式与实测资料的对比......
2025-09-29
-
凸轮机构及从动件的运动规律分析详细阅读
(一)凸轮机构的组成、功用及分类凸轮机构在纺织机械中应用相当广泛。通过凸轮运动曲线的设计，可以达到所要求的各种运动方案，并且结构紧凑。凸轮机构是主要由凸轮、从动件和机架组成。图2-23盘状凸轮机构按凸轮的形状分，凸轮可分为盘形凸轮、圆柱凸轮和移动凸轮，如图2-24 所示。(二)纺织机械中从动件运动规律的选择1.凸轮机构运动线图 从动件的运动规律是指从动件的位移、速度、加速度随凸轮转角的变化规律，如图2-25 所示。......
2025-09-29
-
山区河流卵石推移质公式验证与分析详细阅读
表1-1实测卵石推移质基础资料表1-2为实测的河床质级配，表1-3～表1-5为各测站的水力要素和卵石推移质输沙率按流量分级统计后的资料。图1-4实测推移质输沙率的验证图1-4的对比分析表明，采用修正的Einstein 公式能较好地描述山区河流卵石推移质的运动规律。......
2025-09-29
-
颗粒污泥的性质分析详细阅读
成熟的颗粒污泥，VSS/SS一般为7%～80%，但根据废水性质其范围可在30%～90%。一般来说，反应器沿高度的群落演替遵循9.3.5中所述规律，而单一颗粒污泥的生物构成遵循生物代谢规律，即产酸细菌主要在颗粒表面，产甲烷细菌主要在颗粒内部。......
2025-09-29
-
点的运动方程的分析介绍，详细阅读
x、y 均为时间t 的单值连续函数，即式称为点的直角坐标表示的运动方程。将不同瞬时的t 值代入直角坐标表示的点的运动方程，求出相应的坐标值，即确定了各瞬时点在空间的位置，将它们连接成光滑曲线，即可得到动点的运动轨迹。此外，还可以消去式中的参变量t，得到两坐标间的函数关系这样，也可得到动点的轨迹方程。试求当OA 杆按φ=kt 的规律转动时，点m 的运动方程和轨迹方程。列直角坐标表示的M 点的运动方程。求点M 的轨迹方程。......
2025-09-29
-
如何建立和运行机构的运动分析详细阅读
向机构装置中增加伺服电动机后，便可建立机构的运动分析（定义）并运行。在每个运动定义中，可选择要打开或关闭的伺服电动机并指定其时间周期，以定义机构的运动方式。可以创建多个运动定义，每个定义都使用不同的伺服电动机和锁定不同的图元。图9.5.64 “分析定义”对话框图9.5.65 “电动机”选项卡定义动画时域。在图9.5.64所示的“分析定义”对话框的区域进行下列操作：①输入开始时间：0。在图9.5.64所示的“分析定义”对话框中，单击按钮。......
2025-09-29
- 详细阅读
相关推荐