表面淬火只对表面层进行加热，所以淬火后变形不大，对于精度要求不是很高的齿轮常不需要磨齿。冲击载荷很大时应采用渗碳淬火。渗碳层厚度一般取齿根厚度的 10%～15%，但不大于1.5 mm。但由于硬化层很薄，承载能力不及渗碳淬火齿轮。由于铸铁较脆，为避免载荷集中而引起的齿端局部断裂，齿宽一般应取小些。表6.4常用齿轮材料及其力学特性图3.1-32起动概率随相对水流强度参数的变化趋势......
2025-09-29
推移质颗粒三维运动的平均特性分析
【摘要】：采用三维粒子示踪测速技术，通过分别改变示踪粒子的粒径、比重以及水力比降等条件，观测了10种不同水沙条件下推移质颗粒的三维运动。对推移质颗粒的平均运动规律进行统计分析，探讨粒径、比重及水力比降对推移质运动速度的影响，并分别根据Einstein和Bagnold的研究方法从实测资料得出推移质纵向平均速度的表达式。由图1-12可知，随着坡降的增加，推移质颗粒的速度明显增大，颗粒与水流的相对运动速度减小。
采用三维粒子示踪测速技术，通过分别改变示踪粒子的粒径、比重以及水力比降等条件，观测了10种不同水沙条件下推移质颗粒的三维运动。对推移质颗粒的平均运动规律进行统计分析，探讨粒径、比重及水力比降对推移质运动速度的影响，并分别根据Einstein和Bagnold的研究方法从实测资料得出推移质纵向平均速度的表达式。
1.2.3.1 试验条件
在恒定均匀流的条件下，保持各组试验水深h=5.40cm 不变。10组试验沙样比重γs和静水沉速ω 都由试验实际测量给出，结果见表1-6。
表1-6 水流参数及沙样特性
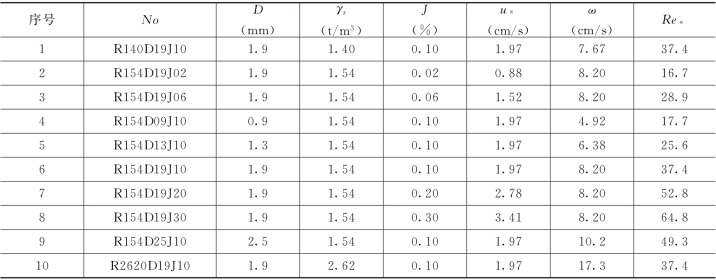
注 D、γs分别为颗粒的粒径、容重;J 为坡降;u为摩阻流速;ω 为实测颗粒沉速;颗粒雷诺数Re=
。
在分析推移质运动规律时，根据Einstein的研究，推移层的厚度定义为2倍粒径。在推移层2D 厚度内将实测资料分成6个流区，各流区的位置见表1-7。
表1-7 颗粒速度分析分区位置
分析实测资料时，首先计算颗粒轨迹的平均高度以判定其所处的流区，求出每个流区中全部颗粒的平均高度和速度，作为该区的代表高度和速度;依次计算各流区的颗粒，得出每组试验推移质颗粒在推移层内三个方向速度的垂线分布。
将各流区颗粒运动速度分布沿垂线积分可得到推移质颗粒的平均运动速度，计算结果见表1-8。
表1-8 颗粒平均速度
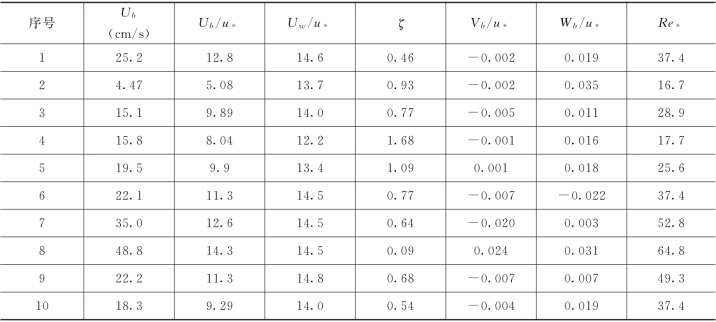
注 Uw为清水平均速度;ζ=Du/ω，其中Du=Uw-Ub为推移质颗粒平均速度与清水平均流速之差;其他符号
同前。
1.2.3.2 颗粒纵向时均速度
1.不同粒径的颗粒纵向平均速度分布
图1-9为不同粒径的颗粒纵向运动速度沿垂线的分布，图中同时画出了相同水流条件下清水的流速分布。试验保持相同的条件，γs=1.54t/m3，水深h=5.4cm，坡降J=0.1%。实测资料表明，在相同水深的条件下，粒径越小，颗粒运动速度越快。对于总体样本来说，在相同的水流条件下，颗粒越粗，推移层的厚度越大，颗粒所在的平均高度越高，粒子垂线平均速度也越大。
若以y/D 为纵坐标观察颗粒纵向速度的分布，见图1-10。从图中可以更清楚地看出，推移层的厚度越大，颗粒的平均速度越快。结合表1 8的资料可以发现，颗粒越粗，推移层越厚，颗粒与水流间的速度差越小，ζ值从1.68 减小到0.68，即ζ 值有随推移层厚度加大而减小的趋势。
2.不同比重的颗粒纵向平均速度分布
其他条件相同，比重不同的推移质颗粒的速度分布见图1-11。由图1-11实测结果可见，颗粒的比重越小，速度越快，其与清水流速的差值就越小。由于ζ 值采用ω 作为无量纲化的参数，虽比重较小时水流与颗粒的速度之差Du较小，但相应的ω 也较小，所以ζ值的变化并不明显。
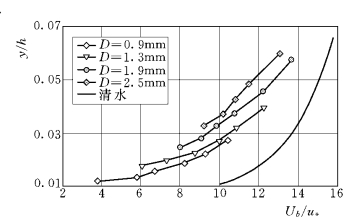
图1-9 不同粒径的颗粒纵向速度分布 (1)
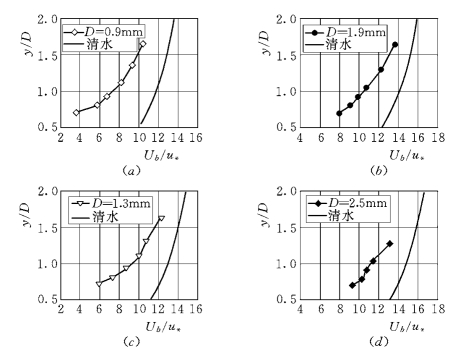
图1-10 不同粒径的颗粒纵向速度分布 (2)
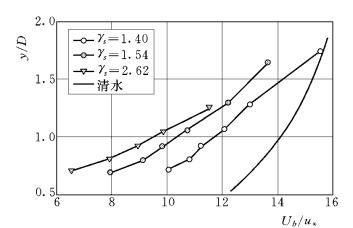
图1-11 不同比重的颗粒纵向速度分布
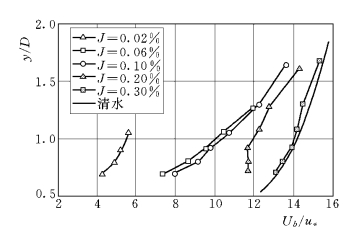
图1-12 不同坡降的颗粒纵向速度分布(https://www.chuimin.cn)
3.不同坡降下颗粒纵向平均速度分布
水深、颗粒容重、粒径都相同，仅坡降不同的5组试验结果见图1-12。
明渠均匀流的坡降越陡，水流的强度越大，为推移质运动提供的能量也越大。由图1-12可知，随着坡降的增加，推移质颗粒的速度明显增大，颗粒与水流的相对运动速度减小。如用u代表水流强度，则ζ值将随u的加大而减小。图1-12的结果表明，在相同的坐标系下，颗粒速度与清水流速的差值随坡度增加而减小，坡降为0.3%时，颗粒速度与清水流速已基本接近。
4.统一规律
试验结果表明，推移质颗粒的运动速度既不是Einstein 假定的11.6u 的常数，表1-8中10组试验平均的Ub/u=10.5，比Einstein的假定偏小;也不是Bagnold 假定的比清水流速小一个ω 值。
采用Bagnold的表述方法，以ζ表示颗粒的相对运动速度，则其与水流强度 (由摩阻流速u体现)和推移层厚度 (2D)具有明显的负相关关系，而比重的影响则反映在ω中。所以ζ应该与沙粒雷诺数Re有关:
将实测资料按上式点绘在图1-13中，相关关系良好，拟合曲线为:
当Re≈24时，Bagnold的假定成立，当Re大于24时，ζ小于1，且随Re的增加而逐渐减小。推移质颗粒运动速度的显函数形式为:
虽然ω 能够反映比重的影响，但在实际应用中各家公式计算的沉速并不一致，试验测量也往往会带入误差，因此引入ω 不如直接采用比重的影响。
图1-13 ζ与Re的关系
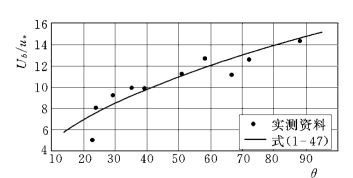
图1-14 颗粒纵向平均速度随θ的变化
若采用Einstein的表述方法进行分析，定义θ=[γ/(γs-γ)]0.5Re，则θ中包含了粒径、比重以及水流强度各项因素，实测的Ub/u与θ之间具有较好的幂函数关系，见图1-14。
1.2.3.3 颗粒的垂向和横向运动速度
颗粒垂向平均速度沿垂线的分布见图1-15，各组试验的垂向平均速度均小于0.2cm/s，说明颗粒在垂向上没有平均运动的趋势，实测数据已属于量测误差的范围。
图1-15 颗粒垂向平均速度沿垂线的分布
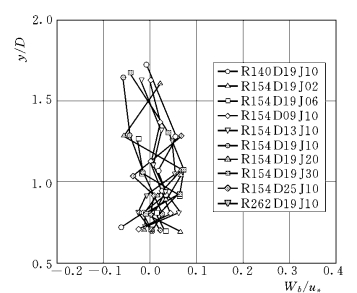
图1-16 颗粒横向平均速度沿垂线的分布
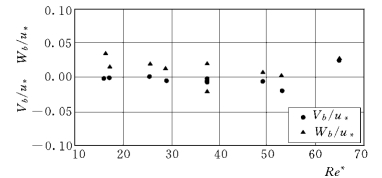
图1-17 颗粒垂向和横向平均速度随Re的变化
图1-16 为颗粒横向平均速度沿垂线的分布，每组实测资料沿垂线的分布随机性摆动较大，但绝对值最大不超过0.3cm/s，可以认为颗粒在横向上没有平均运动趋势。
图1-17为颗粒垂向和横向平均速度随Re的变化，进一步表明了颗粒在两个方向上没有时均运动的趋势。
相关文章
- 详细阅读
-
推移质多年平均输沙量的估计方法详细阅读
但目前由于实测推移质资料短缺，使推移质输沙量直接计算有一定难度，现有估算方法如下。若具有多年推移质资料时，其算术平均值即为多年平均推移质年输沙量。——多年平均流量，m3/s；J——原河道的平均比降，‰；Ms——悬移质输沙量模数，t/km2。......
2025-09-29
-
推导推移质公式详细阅读
推移质公式推求当运动泥沙与床面泥沙的交换达到平衡，即单位时间内自单位床面上冲刷外移的泥沙数量正好与沉积下来的泥沙数量保持相等时的输沙率。Einstein 经过推导得出在单位面积上将有重量为的泥沙被冲刷外移，其中A1、A2为与泥沙颗粒形状有关的系数。图1-2修正的Einstein公式与实测资料的对比图1-2修正的Einstein公式与实测资料的对比......
2025-09-29
-
山区河流卵石推移质公式验证与分析详细阅读
表1-1实测卵石推移质基础资料表1-2为实测的河床质级配，表1-3～表1-5为各测站的水力要素和卵石推移质输沙率按流量分级统计后的资料。图1-4实测推移质输沙率的验证图1-4的对比分析表明，采用修正的Einstein 公式能较好地描述山区河流卵石推移质的运动规律。......
2025-09-29
-
运动关节的类型和特性详细阅读
表4.4不同类型的运动关节及其工作空间所有运动学由于其设计，也由于其加工区域几何结构，表现出不同的特定运动特性。图4.53不同类型的笛卡儿轴系统配置图4.54所示为塑料部件自动装置系统中的笛卡儿搬运系统。与完全标准的运动关节相比，这个市场在统计上更难表现出来。图4.57同一家制造商提供的不同关节臂运动关节当连接多个轴时，很明显，串行轴的精度，即连续连接的轴，对整个系统有重大影响。......
2025-09-29
-
颗粒污泥的性质分析详细阅读
成熟的颗粒污泥，VSS/SS一般为7%～80%，但根据废水性质其范围可在30%～90%。一般来说，反应器沿高度的群落演替遵循9.3.5中所述规律，而单一颗粒污泥的生物构成遵循生物代谢规律，即产酸细菌主要在颗粒表面，产甲烷细菌主要在颗粒内部。......
2025-09-29
-
分析EPC系统的动态特性详细阅读
由系统的传递函数框图可得EPC系统的开环传递函数为式中 k——开环放大系数，。将算得的ωh、ξh、k代入式，可据此画出EPC系统的开环伯德图。图12-18 改造前后CP机组EPC系统的开环伯德图由图12-18可得系统的性能指标为：①穿越频率：ωc=2.4Hz；②幅值裕量：h=16dB；③相位裕度：γ=75°。可见实测值和理论分析值比较接近，说明上面建立的EPC系统的数学模型和确定的参数是正确的，是可以作为预测改造后系统性能的依据的。......
2025-09-29
-
点的运动方程的分析介绍，详细阅读
x、y 均为时间t 的单值连续函数，即式称为点的直角坐标表示的运动方程。将不同瞬时的t 值代入直角坐标表示的点的运动方程，求出相应的坐标值，即确定了各瞬时点在空间的位置，将它们连接成光滑曲线，即可得到动点的运动轨迹。此外，还可以消去式中的参变量t，得到两坐标间的函数关系这样，也可得到动点的轨迹方程。试求当OA 杆按φ=kt 的规律转动时，点m 的运动方程和轨迹方程。列直角坐标表示的M 点的运动方程。求点M 的轨迹方程。......
2025-09-29
相关推荐