表1-1实测卵石推移质基础资料表1-2为实测的河床质级配，表1-3～表1-5为各测站的水力要素和卵石推移质输沙率按流量分级统计后的资料。图1-4实测推移质输沙率的验证图1-4的对比分析表明，采用修正的Einstein 公式能较好地描述山区河流卵石推移质的运动规律。......
2023-06-22
推导推移质公式
【摘要】：推移质公式推求当运动泥沙与床面泥沙的交换达到平衡，即单位时间内自单位床面上冲刷外移的泥沙数量正好与沉积下来的泥沙数量保持相等时的输沙率。Einstein 经过推导得出在单位面积上将有重量为的泥沙被冲刷外移，其中A1、A2为与泥沙颗粒形状有关的系数。图1-2修正的Einstein公式与实测资料的对比图1-2修正的Einstein公式与实测资料的对比
推移质公式推求当运动泥沙与床面泥沙的交换达到平衡，即单位时间内自单位床面上冲刷外移的泥沙数量正好与沉积下来的泥沙数量保持相等时的输沙率。
1.1.2.1 泥沙的沉积率
Einstein (1950)假定在一定的水流条件下，河床表面比例为P 的部分面积上的水流上举力大于泥沙颗粒的水下重量，有1-P 的面积上的上举力小于泥沙的水下重量。经过推导后得出，如泥沙颗粒的单步距离为L，则泥沙的平均运动距离L0为:
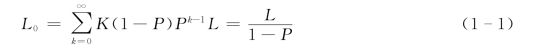
颗粒的重力(γs-γ)D 3越大，跃起后落回床面越快，其单步距离越短;水流作用力λ2ρD 2u 2*越大，颗粒跳起后运动的单步距离越长。可以假定颗粒运动的单步距离与水流作用力成正比而与颗粒的水下重力成反比:
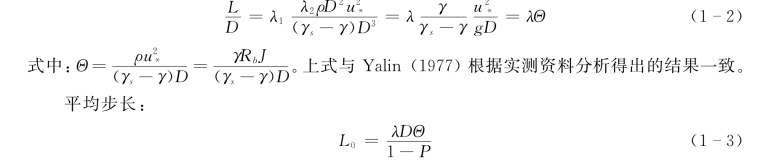
若推移质泥沙的单宽输沙率为gb，则在单位时间内通过所研究断面的泥沙都将在长度为L0的范围内沉积下来，这样，单位面积上泥沙的沉积率gd为:
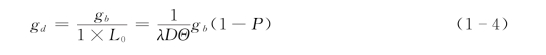
1.1.2.2 泥沙的冲刷率
泥沙颗粒自床面冲刷外移的条件取决于有多少这样的泥沙暴露在水流下面，以及使泥沙举离床面的上举力大于沙粒水下重量的或然率有多大。Einstein 经过推导得出在单位面积上将有重量为
的泥沙被冲刷外移，其中A1、A2为与泥沙颗粒形状有关的系数。
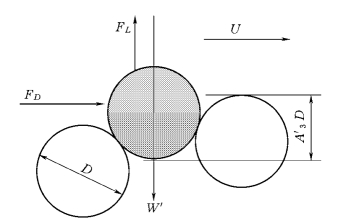
图1-1 沙粒在床面的位置
已知冲刷外移的沙量，需要进一步求出这些泥沙被冲起的时间。Einstein 取t=A3D/ω。但一般认为，颗粒被举离床面的时间应该与水流条件有关。假定颗粒位于床面的位置如图1-1所示。
当水流的上举力FL大于颗粒的水下重量时，颗粒被向上抬升，当抬升的高度到达A′3D，颗粒就会在拖曳力FD的作用下开始运动。根据胡春宏(Hu和Hui，1996)的研究，颗粒从床面被举离的速度与u*成正比，则颗粒被举离床面的时间可表示为:
最后得出单位面积上泥沙的冲刷率:
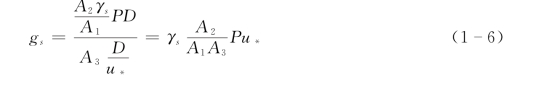
1.1.2.3 输沙平衡条件
当推移质运动达到平衡时，自河床冲起的泥沙和推移质中落淤的泥沙应相等，由式(1-4)和式(1-6)可得:
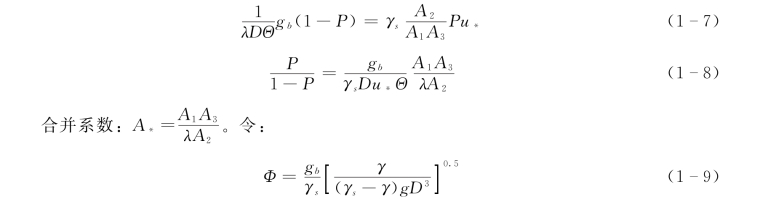
为输沙强度参数，则:
或:
1.1.2.4 水流条件与泥沙运动概率的关系
泥沙的水下重量为:水流作用在颗粒上的上举力为:
Einstein和El-Samni(1949)从试验结果得出，若取距理论床面0.35D 处的流速作为上式中的有效流速，则CL=0.178，上举力的脉动遵循正态分布:
式中:η为随时间而变化的上举力脉动值，如用上举力脉动的标准差η0来衡量上举力的大小，即令η=η0η*，其中η*为无量纲的上举力脉动值，再令:
或然率P 代表W′/FL小于1的机遇:
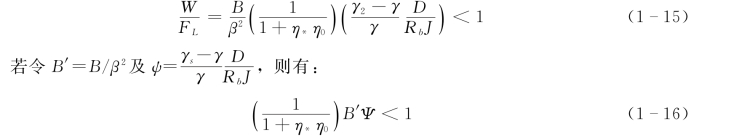
若考虑水流上举力的值大于颗粒的水下重量时泥沙开始运动，即:
临界状态时，得出泥沙开始运动的水流条件下限值:
式中B*=B′/η0，运动泥沙的概率:
由式(1-11)得:
根据实测资料得出B*=0.07，1/η0=2，A*=16，则:
式(1-21)与实测资料的对比见图1-2。图中同时画出了Einstein公式和Meyer Peter公式(1948)，可以看出修正的Einstein公式与实测资料一致，特别是高强度输沙时与实测资料符合良好。
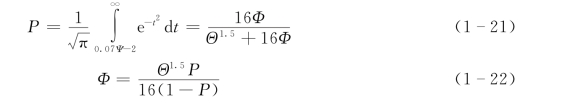
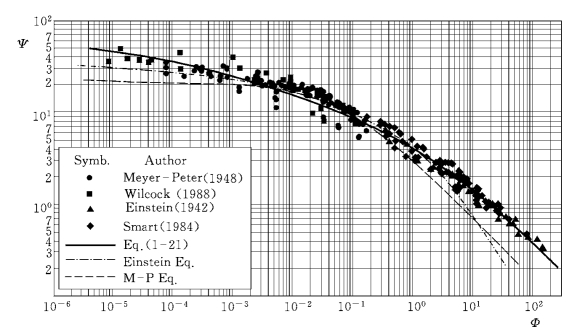
图1-2 修正的Einstein公式与实测资料的对比
有关泥沙研究进展的文章
- 详细阅读
-
推移质起动概率分析详细阅读
表面淬火只对表面层进行加热，所以淬火后变形不大，对于精度要求不是很高的齿轮常不需要磨齿。冲击载荷很大时应采用渗碳淬火。渗碳层厚度一般取齿根厚度的 10%～15%，但不大于1.5 mm。但由于硬化层很薄，承载能力不及渗碳淬火齿轮。由于铸铁较脆，为避免载荷集中而引起的齿端局部断裂，齿宽一般应取小些。表6.4常用齿轮材料及其力学特性图3.1-32起动概率随相对水流强度参数的变化趋势......
2023-06-21
-
角度变换公式推导详解详细阅读
图6.10坐标系旋转如图6.10所示，假定在车体处于初始水平位置时，火炮的指向为此时炮塔系统的方位角为φ，俯仰角为θ。图6.10坐标系旋转上述坐标旋转的顺序不唯一，α、β以及γ排列的六种旋转次序都会使火炮的最终指向为。令则可以得到的表达式同时，角∠Z0Z2P0的表达式为在球面三角Z0P0Z2中，已知。下一节将在这一前提下，建立无人炮塔的动力学模型。......
2023-06-24
- 详细阅读
-
桥涵水文学-推移质输沙率详细阅读
起动流速是推移质运动产生的条件，沙波运动是推移质运动的主要形式，而推移质运动的强烈程度则用推移质输沙率来表示。推移质输沙率的大小，对河流的冲刷和淤积有着重要意义。推移质输沙率的计算方法，有几种不同的研究途径。目前我国的桥下一般冲刷中，采用以流速为主要参数的推移质输沙率公式，这种计算方法认为影响推移质输沙率的主要因素是水流的流速。......
2023-11-20
-
重新推导基于Einstein公式的泥沙输移模详细阅读
Einstein于1942年提出了输沙强度参数Φ 与水流参数Ψ 之间的经验关系，1950年又推导出了严格的数学表达式，Einstein公式在河流工程界得到了广泛的应用。在处理泥沙输移的复杂现象时，Einstein 进行了一些经验性的简化假定:推移质颗粒运动的单步步长为与粒径成正比的常数，不受水流条件的影响，对于圆形颗粒，单步步长为颗粒直径的100倍。本章遵循Einstein的基本思路，对颗粒沉降、起动概率和水流作用力等进行了重新推导，得出了修正的Einstein公式。......
2023-06-22
-
推移质颗粒单步运动的统计规律分析详细阅读
分析具有代表性的6组试验的推移质颗粒的单步运动，对大量粒子的运动规律进行统计分析。图1-34典型跃移轨迹xz平面图1-33、图1-34中L 为粒子跃移的单步步长，L1为颗粒起跃至达到最高点的长度，H 为跃高，d 是颗粒单步运动横向摆动幅度，uo、vo、wo分别为起跃点的纵向、垂向和横向速度，ue、ve、we则为降落点的纵向、垂向和横向速度。......
2023-06-22
-
推移质多年平均输沙量的估计方法详细阅读
但目前由于实测推移质资料短缺，使推移质输沙量直接计算有一定难度，现有估算方法如下。若具有多年推移质资料时，其算术平均值即为多年平均推移质年输沙量。——多年平均流量，m3/s；J——原河道的平均比降，‰；Ms——悬移质输沙量模数，t/km2。......
2023-06-21
相关推荐