卷取机构包括卷取和卷布两部分。 连续式卷取机构的卷取动作是由织机主轴或直接由卷取电动机，经减速机构传动，使卷布辊连续回转。 机械式卷取机构由织机主轴或筘座等，通过齿轮等机械传动装置驱动卷布辊运动。......
2025-09-29
模拟式电压表的工作原理及分类
【摘要】：模拟式电压表分为均值电压表、峰值电压表和有效值电压表三种。均值电压表一般采用放大-检波式电路组成低频电压表，或采用外差式电路组成高频微伏表。由于电流表动圈转动的惯性，其指针将指示Iout 的值。为了不因电压表的接入而对被测电路产生较大影响，在检波前要加入跟随器进行隔离。1）检波器电路对于任意波形的周期性交流电压，在所观察的时间或一个周期内，其电压所能达到的最大值即称为峰值，用Up表示。
模拟式电压表分为均值电压表、峰值电压表和有效值电压表三种。
1.均值电压表
在均值型电压表内，电压的平均值指被测电压经检波后的平均值，这通常是对全波检波而言，即输入电压的绝对值在一个周期的平均值。
均值电压表一般采用放大-检波式电路组成低频电压表，或采用外差式电路组成高频微伏表。
1）检波器电路
电子电压表内常用的均值检波器电路如图5-15所示，图（a）为桥式电路，图（b）中使用了两只电阻代替图（a）中的两只二极管，称为半桥式电路。
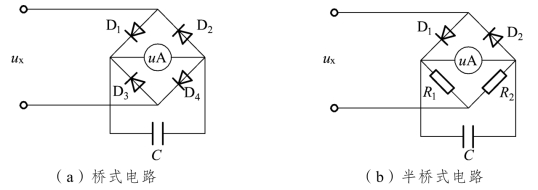
图5-15 均值检波器原理图
均值响应检波器输出平均电流Iout 正比于输入电压的平均值。由于电流表动圈转动的惯性，其指针将指示Iout 的值。为了使指针稳定，在表头两端跨接滤波电容，滤去检波器输出电流中的交流成分，如图5-16所示。
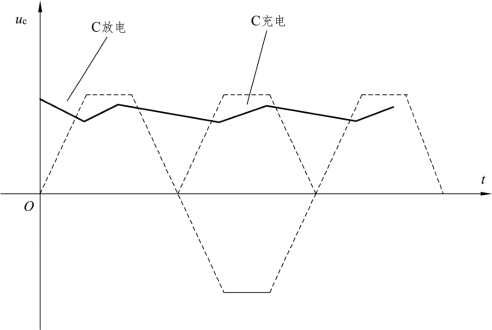
图5-16 电容滤波示意图
2）定度系数和波形换算
考虑到正弦波是最基本的和应用最普通的波形，以及有效值的实际意义，几乎所有的交流电压表都是按照正弦波电压有效值定度的。显然，如果检波器不是有效值响应，则有标称值（即示值Uα）与实际响应值之间存在一个系数，此系数即为定度系数，记作Kα。
对于均值响应检波器，在额定频率下加正弦波电压时的示值
所以
由此可知，如果用均值电压表测量纯正弦波电压，其示值Uα就是被测电压正弦波的有效值。如果被测电压是非正弦波电压时，其示值并无直接的物理意义，只有把示值经过换算后，才能得到被测电压的有效值。
首先按“平均值相等示值也相等”的原则将示值Uα折算成被测电压的平均值：
再用波形因数Kf（如果被测电压的波形已知）求出被测电压的有效值：
综上所述，波形换算的方法是：当测量任意波形电压时，将测量结果（即表盘上的示值）先除以定度系数折算成被测电压的平均值，再乘以被测电压的波形因数（如果被测电压的波形已知）即可得到被测的非正弦电压有效值。
对于采用全波检波电路的电压表来说
【例5-1】 用全波式均值表分别测量方波及三角波电压，示值均为1 V，问被测电压的有效值分别为多少？
解：（1）对于方波
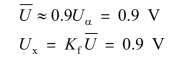
（2）对于三角波
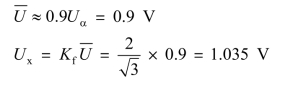
2.峰值电压表
测量高频电压一般不用均值电压表和有效值电压表，原因是它们的检波器件在测量时导通时间较长，因而其输入阻抗较低。为了不因电压表的接入而对被测电路产生较大影响，在检波前要加入跟随器进行隔离。测量高频电压时，由于放大器的带宽限制，会产生较大的频率误差。为了避免这种情况，常采用检波-放大式电压表来测量高频电压，将被测交流信号首先通过探极进行检波，使其变成直流电压，然后再放大。这种电压表多为峰值电压表，其检波器为峰值检波器。
1）检波器电路
对于任意波形的周期性交流电压，在所观察的时间或一个周期内，其电压所能达到的最大值即称为峰值，用Up表示。对于正弦波而言，峰值就等于其振幅值Um。
峰值响应检波器电路如图5-17所示。其中，图（a）为串联式，图（b）为并联式，其电路形式与均值响应检波器无显著差别，但其参数选取必须满足：
式中 Tmax——被测交流电压的最大周期；
Tmin——被测交流电压的最小周期；
RΣ——信号源内阻和二极管正向电阻之和。
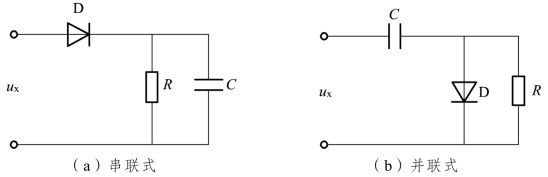
图5-17 峰值检波器电路
这样的电路参数使检波器输出电压平均值
近似等于输入电压ux(t)的峰值。
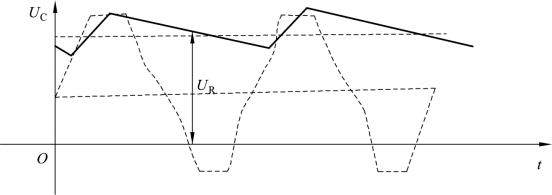
图5-18 串联式原理示意图
在图5-17（a）中因为电容C充电时间短放电时间长，从而保持其两端的电压始终接近于输入电压的峰值，即
如图5-18所示。
在图5-17（b）所示的并联峰值检波器中，ux(t)正半周通过二极管D给电容迅速充电，而负半周C两端电压缓慢向R放电，使
如图5-19所示。
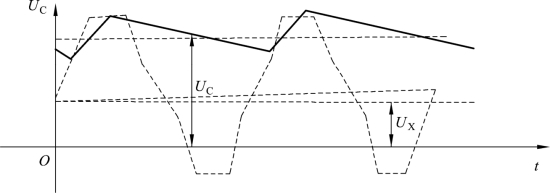
图5-19 并联式原理示意图
上述两种电路相比较，并联式检波电路中的电容C还起着隔直流的作用，便于测量含有直流成分的交流电压。但R上除直流电压外。还叠加有交流电压，增加了额外的交流通路，故其输入电阻低于串联式电路。
2）定度系数及波形换算方法
峰值表和均值表类似，一般也是按正弦波有效值进行定度，在额定频率下度盘的示值(https://www.chuimin.cn)
式中，Kα是定度系数。
因为以正弦波有效值定度，所以，
式中，UP及U分别表示正弦波的峰值及有效值。
根据波峰因数的定义，正弦波的波峰因数为
即定度系数的倒数。而方波的KP＝1，三角波的
均值电压表的原理相同，当用峰值电压表测量非正弦波电压时，其示值没有直接的物理意义。按照“示值相等峰值也相等”的原则，将示值除以定度系数Kα得到被测电压的峰值，再利用波峰因数换算成被测电压ux(t)的有效值Ux。具体步骤如下：
【例5-2】 用峰值电压表分别测量方波和三角波电压，示值均为10 V。求被测电压的有效值是多少伏？
解：（1）对于方波：
（2）对于三角波：
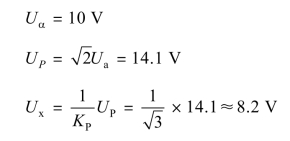
3.有效值电压表
电压有效值的定义是
有效值检波器输出对应被测信号的有效值，即Uo（t）∝Ux；考虑有效值的定义，为方便也可使检波器输出对应被测信号有效值的平方，即Uo（t）∝UX2。可以有以下三种方案。
1）检波式有效值电压表
如果通过检波器来实现，就要求这种检波器具有平方律关系的伏安特性。图5-20给出一种基本电路形式。
图（a）利用二极管正向特性曲线的起始部分，得到近似平方关系。选择合适的偏压E0（大于被测电压ux（t）的峰值），可得到图（b）所示波形图。
设检波二极管D的检波系数为k，则流过它的电流
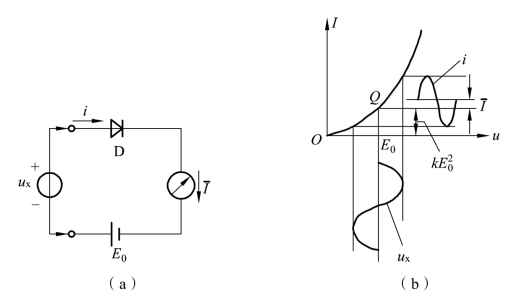
图5-22 平方律特性的获得
直流电流表指针的偏转角与电流I的平均值I成正比：
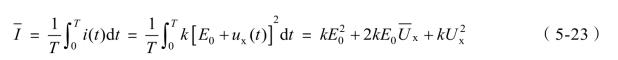
式中 kE20——静态工作点电流，即无信号输入时的起始电流；
——被测电压的平均值，对于正弦波或周期性对称的电压Ux＝0；
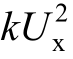——与被测电压有效值平方成比例的电流平均值（I）。
先设法在电路中抵消起始电流，则送到直流电流表电流为
从而实现了有效值转换。
用这种有效值响应检波器所构成的有效值电压表，在理论上可以测量任意周期性波形电压的有效值，不会产生波形误差。但当用正弦波电压有效值刻度时，表盘刻度是非线性的，因为I和Ux的平方成正比。
2）热电转换式有效值电压表
热电转换式电压表是实现有效值电压测量的一种重要方法。它利用具有热电变换功能的热电偶来实现有效值变换。
图5-23是热电转换电压表的示意图。图中，AB为不易熔化的金属丝，称为加热丝，M为热电偶，它由两种不同材料的导体连接而成，其交界面与加热丝耦合，故称“热端”，而D、E为“冷端”。当加入被测电压ux时，热电偶的热端C点温度将高于冷端D、E，产生热电动势，故有直流电流流过微安表。该电流正比于热电动势。因为热端温度正比于被测电压有效值Ux的平方，热电势正比于热、冷端的温度差，因而通过电流表的电流I将正比于Ux2。这就完成了被测交流电压有效值到热电偶电路中直流电流之间的变换，从广义来讲，也就完成了有效值检波。
图5-24所示为热电式有效值电压表简化组成方框图，它采用热电偶作为AC/DC变换元件。其中M1为测量热电偶，M2为平衡热电偶。
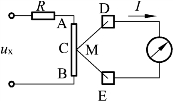
图5-23 热电转换原理
图5-24 热电式有效值电压表原理框图
被测电压ux(t)经宽带放大器放大后加到测量热电偶M1的加热丝上，经热电变换得热电动势Ex，它正比于被测电压有效值Ux的平方，即
式中，A1为宽带放大器电压放大倍数；K为热电偶转换系数。
平衡热电偶M2与M1的性能相同，其作用有二：一是使表头刻度线性化，二是提高热稳定性。在被测电压经放大后加到M1的同时，经直流放大器放大后的输出电压也加到平衡热电偶M2上，产生热电动势Ef＝KUo2 ut。当直流放大器的增益足够高且电路达到平衡时，其输入电压Uin=Ex-Ef ≈0，即Ex＝Ef，所以Uout＝A1Ux。由此可知，如两个热电偶特性相同（即K相同），则通过图示反馈系统，输出直流电压正比于ux(t)的有效值Ux。所以，表头示值与输入呈线性关系。
这种仪表的灵敏度及频率范围取决于宽带放大器的带宽及增益，表头刻度线性，基本没有波形误差。其主要缺点是有热惯性，使用时需等指针偏转稳定后才能读数，而且过载能力差，容易烧坏，使用时应注意。
3）计算式有效值电压表
交流电压的有效值即其均方根值。根据这一概念，利用模拟电路对信号进行平方、积分、开平方等运算即可得到测量结果。
图5-25所示为计算式转换器方框图。第一级为模拟乘法器；第二级为积分器；第三级对积分器的输出电压进行开方使输出电压大小与被测电压有效值成正比，从而得到最后测量结果。
图5-25 计算式有效值电压表方框图
相关文章
- 详细阅读
-
数字万用表的工作原理解析详细阅读
图8.3-139V电池及电池扣12.9V电池及电池扣如图8.3-13所示，该数字万用表使用9V电池作为电源。除OFF挡外，其余各挡位均处于接通状态，保证万用表的正常供电。图1-162图8.3-17数字万用表的电路原理图电源采用9V电池供电，负极连接到ICL7106的V-端，正极经电源开关V型弹片KL后连接到ICL7106的V+端和电路图中标有VCC的位置。数字万用表的核心是3 1/2位A/D转换器ICL7106。......
2025-09-29
-
综述：继电器的结构、工作原理及应用选用详细阅读
继电器是根据某种特定形式的输入信号接通或断开小电流控制电路，实现远距离自动控制和保护的自动电器。按用途可分为控制和保护继电器。图1-23 继电器特性1.熟悉继电器的结构和工作原理及其用途。......
2025-09-29
-
STM仪器的构造及工作原理详细阅读
图3-40管状压电器件1.机械部分压电控制扫描器、距离控制器和扫描装置统称为STM中的机械部分，为了得到高性能的STM，对各部分控制器都有一定的要求。在STM测试时必须隔绝的两种扰动类型是震动和冲击。由于钨针尖能够满足STM仪器刚性的要求，因而被广泛地使用。......
2025-09-29
-
传感器分类：测量对象和工作原理详细阅读
传感器的分类方法很多，但常用的分类方法有两种：一种是按测量对象分类，如温度传感器、湿度传感器、力传感器、位移传感器、速度传感器等；另一种是按传感器的工作原理分类，如热电式传感器、电容式传感器、压电式传感器、磁电式传感器等。结构性传感器因被测参数的变化引起传感器的结构变化，导致输出电量的变化，它是利用物理学中的场定律和运动定律等构成，如电容式传感器、电感式传感器。......
2025-09-29
-
变频器的调速原理及分类详细阅读
图4-1列出了几种常见的变频器。当主电路出现电压不正常或输出电流过大时，控制电路通过检测电路获得该情况后，会根据设定的程序作出相应的控制，如让变频器主电路停止工作，并发出相应的报警指示。从图中可以看出，交-交型变频器与交-直-交型变频器的主电路不同，它采用交-交变频电路直接将工频电源转换成频率可调的交流电源的方式进行变频调速。......
2025-09-29
-
放电式延时电路工作原理及应用详细阅读
放电式延时电路和充电式延时电路相比较，放电式延时电路能获得较长的延时，且延时准确性比较高。它属于延时动作、瞬时复归电路。图2-53放电式延时电路工作原理：正常时，没有信号输入，三极管VT1基极负偏压而截止，其集电极为高电位。其集电极电位立即降到近于零，这时由于VT1也饱和导通，其集电极为低电位，所以三极管VT3便没有提供基极电流的回路，立即变为截止，输出Usc为高电位。......
2025-09-29
-
电渗析的工作原理及应用详细阅读
电渗析过程的原理如图6-15所示，该过程使用带可电离的活性基团膜从水溶液中去除离子。与此同时，在电极和溶液的界面上，通过氧化、还原反应，发生电子与离子之间的转换，即电极反应。发生的电极反应如下：图6-15电渗析原理示意图所以，在阴极不断排出氢气，在阳极则不断有氧气或氯气放出。在电渗析过程中，电能的消耗主要用来克服电流通过溶液、膜时所受到的阻力以及进行电极反应。......
2025-09-29
相关推荐