如测量人员技术不熟练,量具使用不当或者视力较差等原因引起的测量误差。1)随机误差及其处理随机误差是指在同一测量条件下,多次测量同一被测量时,误差的绝对值和符号没有确定变化规律的误差。④抵偿性随着测量次数的增多,随机误差的算术平均值趋于零。实验对比法是用不同的仪器进行测量,通过对比测量结果发现系统误差的方法。......
2023-06-15
测量数据的处理,就是从测量得到的原始数据中求出被测量的最佳估计值,并计算其精确程度。测量结果通常用数字或图形图像等形式表示。用数字方式表示的测量结果,可以是一个数据,也可以是一组数据;用图形图像方式表示的测量结果,可以是将测量中数据处理后绘制的图形,也可以是显示在屏幕上的图像,具有形象、直观的特点,如放大器的幅频特性曲线等。
测量中要记录数据并进行运算,记录的数据应取几位,运算后应保留几位,这些要由误差范围来决定,也涉及有效数字的问题。
1.有效数字的概念
任何一个测量量,既然其测量结果都包含有误差,该测量的数值就不应该无限制地写下去。例如,(1.3682···±0.02)cm应写成(1.37±0.02)cm,因为误差范围0.02 cm可知,该数值在百分位上已有误差,在它以后的数字便没有意义了。因此,测量结果只写到有误差的那一位数,并且在该位数以后按“四舍五入”的法则取舍。最后一位虽然有误差,但在一定程度上也能反映出被测量的客观大小,也是有效的。我们把能反映出被测量实际大小的全部数字,称为有效数字。或者说,把测量结果中可靠的几位数字加上有误差的一位数字,统称为测量结果的有效数字。有效数字的个数叫作有效数字的位数,如上述的1.37 cm称为三位有效数字。
有效数字的位数与十进制单位的变换无关,即与小数点的位置无关。因此,用于表示小数点位置的0不是有效数字。当0不是用于表示小数点位置时,0和其他数字具有同等地位,都是有效数字。显然,在有效数字的位数确定时,第一个不为零的数字左面的零不能算有效数字的位数,而第一个不为零的数字右面的零一定要算作有效数字的位数。如0.0135 m是三位有效数字,0.0135 m、1.35 cm及13.5 mm三者是等效的,只不过是分别采用了米、厘米和毫米作为长度的表示单位;1.030 m是四位有效数字。从有效数字的另一面也可以看出测量用具的最小刻度值,如0.0135 m是用最小刻度为毫米的尺子测量的,而1.030 m是用最小刻度为厘米的尺子测量的。因此,正确掌握有效数字的概念对测量来说是十分必要的。
由于数据的最后一位有效数字一般是估测的,所以称为欠准数字或不可靠数字,而其他有效数字均为准确数字或可靠数字。例如,某电流值为0.0321 mA,其中“3、2、1”三个数字为有效数字,两个“0”为非有效数字,“1”为欠准数字,“3、2”为准确数字。
有效数字的位数多少大致反映相对不确定度的大小。有效数字位数越多,相对不确定度越小,测量结果的精确度越高。
2.有效数字的处理
在实际测量中,经常要对测量结果的几个数据的有效数据进行必要的处理,然后进行运算。保留的有效数字位数过多或过少,都会影响最后的结果。保留位数的总原则是:运算过程中有效数字的位数应按其中准确度最差的数据的有效数字进行取舍。
1)运算数据尾数的取舍规则
为了使舍和入的概率相等,现在通用的规则是“四舍六入五凑偶数”。即大于5的数,向前入1;小于5的数,舍去;而等于5的数要看5后面是否有数字:若5后有数字,则舍5入1。若5后面没有数字或为0,那么5之前是奇数则舍5入1,是偶数则舍去5。
【例4-4】 以下数字均保留小数点后一位有效数字:
10.34→10.3(舍去4);
10.36→10.4(舍6入1);
10.35→10.4(5后面无数字,5前面3为奇数,5入1);
10.45→10.4(5后面无数字,5前面4为偶数,舍5);
9.150→9.2(5后面为0,前面是奇数,舍5入1);
8.251→8.3(5后面有数字,舍5入1)。
每个数字经舍入后,末位是欠准数字,末位之前是准确数字,最大舍入误差是末位的一半。因此当测量结果未注明误差时,就认为最末一位数字有“0.5”误差,称此为“0.5误差法则”。
【例4-5】 用一台0.5级电压表100 V量程挡测量电压,电压表指示值为85.35 V,试确定有效位数。
解:该表在100 V档最大绝对误差
![]()
绝对误差为±0.5 V,应用0.5误差法则,测量结果的末位应是个位,测量值为85 V。
2)加法或减法运算
对于加减类型的运算,运算结果的末位应与参与运算的有效数字中最后一位的位数最高的分量相同,或者说是以小数点后有效数字位数最少的那一项为准。例如:
![]()
推论:若干个直接测量值进行加法或减法计算时,选用精度相同的仪器最为合理。
3)乘法和除法运算 对于乘除类型的运算,运算结果的有效数字位数应与参与运算有效数字位数最少的分量相同。例如:
![]()
推论:测量的若干个量,若是进行乘法除法运算,应按照有效位数相同的原则来选择不同精度的仪器。
4)乘方和开方运算
乘方和开方运算的有效数字的位数与其底数的有效数字的位数相同。例如:
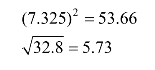
6)三角函数、对数和指数运算
三角函数、对数和指数运算,其结果的有效数字位数一般与变量的位数相同。例如:
![]()
则
![]()
结果为
![]()
有关传感检测与电子测量的文章

如测量人员技术不熟练,量具使用不当或者视力较差等原因引起的测量误差。1)随机误差及其处理随机误差是指在同一测量条件下,多次测量同一被测量时,误差的绝对值和符号没有确定变化规律的误差。④抵偿性随着测量次数的增多,随机误差的算术平均值趋于零。实验对比法是用不同的仪器进行测量,通过对比测量结果发现系统误差的方法。......
2023-06-15

为了对测量结果的误差进行估算,我们用约定真值来代替真值求误差。例如,用同一仪器测量10m 长相差1mm 与测量100m长相差1mm,其绝对误差相同。显然,只有绝对误差还难以评价测量结果的可靠程度,因此引入相对误差的概念。在近似情况下,相对误差也往往表示为绝对误差与测量值之比。相对误差常用百分数表示,即如果待测量有理论值或公认值,也可用百分差来表示测量的好坏,即绝对误差、相对误差和百分差通常取1~2位有效数字来表示。......
2023-11-02

为了减小或消除系统稳态误差,可以增加积分环节的个数,或增大开环增益。在保证系统稳定的前提下,为实现提高稳态精度,可采用复合控制的措施来减小稳态误差。显然,增加扰动补偿的复合控制,只要选取适当的补偿环节,可以减小甚至消除扰动信号引起的稳态误差,且扰动补偿复合控制也不改变原系统的稳定性。......
2023-06-28

在何种情况下,水银压力计的测量误差可以忽略不计?水银压力计的测量值比实际压力略小。这是因为毛细现象使测压管内的水银液面下降导致了测量误差。......
2023-06-29

2)随机误差对同一被测量进行多次重复测量时,若误差的大小随机变化,不可预知,这种误差称为随机误差,又称偶然误差。随机误差的特点是:在测量次数测量足够时,其总体服从统计规律,它反映测量值离散性的大小,所以说随机误差的大小表明测量结果的精密度。产生随机误差的原因主要有机械干扰、环境干扰、电磁场变化、放电噪声、光和空气及系统元件噪声等。可以采用对多次测量值取算术平均值的方法来减小随机误差的影响。......
2023-06-22

测量仪器仪表的测得值与被测量真值之间的差异,称为测量误差。为了表征测量的准确程度,常用相对误差的形式。例如5.0级表示满度相对误差的最大值不超过仪表量程上限的5%。解:0.5级温度计测量时可能出现的最大绝对误差、测量80 °C可能出现的最大实际相对误差分别为该温度计的满度相对误差介于1.0%与1.5%之间,因此该表的精度等级应等为1.5级。......
2023-06-22

从自身参数可以看出,激光跟踪仪的测距精度远高于测角精度,而且随着测量距离的增大,测角误差增大更为明显,符合表1中的观测结果。如图2所示,在Matlab中利用激光跟踪仪自身参数把随机误差注入到观测值中,以模拟点云的形式得到三维坐标的点云分布图。查定额《配合比参考表》,砾石GD40中砂425水泥C15商品混凝土参考价为135.66元/m3,则:图2 激光跟踪仪测量点云分布图......
2023-06-23

采用往返观测的方法,取成果的中数,可减弱其影响。为了防止水准仪和尺垫下沉,测站和转点应选在土质坚实处,并踩实三脚架和尺垫,使其稳定。......
2023-08-20
相关推荐