UASB反应器中废水为上向流，最大特点是在反应器上部设置了一个特殊的气、液、固三相分离系统，三相分离器的下部是反应区。气、液、固的混合液上升至三相分离器内，气体可被收集，污泥和水则进入上部相对静止的沉淀区，在重力作用下，水与污泥分离，上清液从沉淀区上部排出，污泥被截留在三相分离器下部并通过斜壁返回到反应区内。图9-8UASB反应器中沿高度的污泥浓度分布示意图较低水力负荷；较高水力负荷......
2025-09-29
电容式传感器的工作原理
【摘要】：电容式传感器的工作原理可以从图2-16所示的平板式电容器中得到说明。固定3个参量中的任意2个，可做成3种类型的电容传感器。图2-18所示为变极距型电容式传感器结构原理图。电容式传感器的灵敏度用S表示，其计算公式为电容C与间隙δ之间的变化特性如图2-19所示。于是传感器总的电容量C应等于两个电容C1和C2的并联之和，即3.变介电常数型电容式传感器变介电常数型电容式传感器的结构原理如图2-20所示。
电容式传感器是以不同类型的电容器为传感元件，并通过电容传感元件把被测物理量的变化转换成电容量的变化，然后再经转换电路转换成电压、电流或频率等信号输出的测量装置。
电容式传感器的工作原理可以从图2-16所示的平板式电容器中得到说明。由物理学可知，由两平行极板所组成的电容器如果不考虑边缘效应，其电容量为
式中 A——两极板相互遮盖的面积（mm2）；
δ——两极板之间的距离（mm）；
ε——两极板间介质的介电常数（F/m）。
由式（2-25）可得，当被测量使A、δ、ε 3个参数中任何1项发生变化时，电容量就会随之发生变化。固定3个参量中的任意2个，可做成3种类型的电容传感器。
图2-16 平板电容器
1.变面积型电容式传感器
变面积型电容传感器的结构原理如图2-17所示。图中（a）、（b）为单边式，（c）为差分式；（a）、（b）也可做成差分式。图中1、3为固定板，2是与被测物相连的可动板，当被测物体带动可动板2发生位移时，就改变了可动板与固定板之间的相互遮盖面积，并由此引起电容量C的变化。
对于如图2-17（a）所示的平板式单边直线位移式传感器，若忽略边缘效应，其电容变化量为
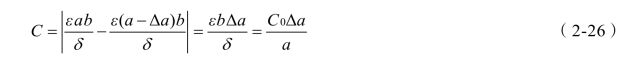
图2-17 变面积型电容式传感器结构原理图
式中 b——极板宽度；
a——极板起始遮盖长度；
Δa——动极板位移量；
ε——两极板间介质的介电常数；
δ——两极板间的距离；
C0——初始电容量。
这种平极单边直线位移传感器的灵敏度S为
对于如图2-17（b）所示的单边角位移型传感器，若忽略边缘效应，则电容变化量为
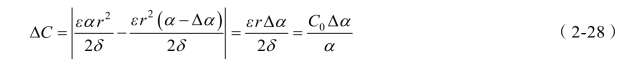
式中 α——覆盖面积对应的中心角度；
r——极板半径；
Δα——动极板的角位移量。
这种单边角位移式传感器的灵敏度为(https://www.chuimin.cn)
式中 A0——电容器起始覆盖面积；
θ——动板的角位移量。
实际应用时，为了提高电容式传感器的灵敏度，减小非线性，常常把传感器做成差分式，如图2-17（c）所示。中间的极板2为动板，上、下两块（即板1和3）为定板。当动板向上移动一个距离x后，上极距就要减少一个x，而下极距就要增加一个x，从而引起上、下电容变化。差接后的这种传感器灵敏度可提高一倍。
2.变极距型电容式传感器
图2-18所示为变极距型电容式传感器结构原理图。图中1和3为固定极板，2为可动极板（或相当于可动极板的被测物），其位移由被测物体带动。从图4-3（a）、（b）可看出，当可动极板由被测物带动向上移动（即δ减小）时，电容值增大，反之电容值则减小。
图2-18 变极距型电容式传感器结构原理图
设极板面积为A，初始距离为δ0，以空气为介质时，电容量C0为C0＝ε0A/δ0。
当间隙δ0减小Δδ变为δ时（设Δδ << δ0），电容C0增加ΔC变为C，即
电容C与间隙δ之间的变化特性如图2-19所示。电容式传感器的灵敏度用S表示，其计算公式为
图2-19 C-δ 特性曲线图
在实际应用中，为了改善其非线性、提高灵敏度和减小外界的影响，通常采用图2-18（c）所示的差分式结构。这种差分式传感器与非差分式的相比，灵敏度可提高一倍，且非线性误差大大降低。差分式电容式传感器的灵敏度计算公式为
3.变介电常数型电容式传感器
变介电常数型电容式传感器的结构原理如图2-20所示。其中图2-20（a）中的两平行极板为固定板，极距为δ0，相对介电常数为εr2的电介质以不同深度插入电容器中，从而改变了两种介质极板的覆盖面积。于是传感器总的电容量C应等于两个电容C1和C2的并联之和，即
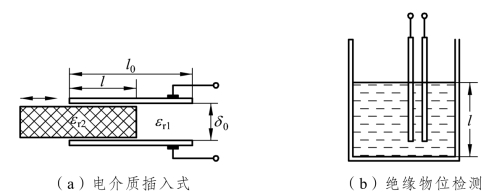
图2-20 变介电常数型电容式传感器
式中 l0，b0——极板的长度和宽度；
l——第二种介质进入极板间的长度。
当介质1为空气，l＝0时，传感器的初始电容C0＝ε0εrl0b0/δ0；当介质2进入极板间l距离后，所引起电容的相对变化为
可见，电容的变化与介质2的移动量l呈线性关系。
上述原理可用于非导电绝缘流体材料的位置测量。如图2-20（b）所示，将电容器极板插入被监测的介质中。随着灌装量的增加，极板覆盖面也随之增大，从而测出输出的电容量。根据输出电容量的大小即可判定灌装物料的高度l。
说明：当极板间有导电物质存在时，应选择电极表面涂有绝缘层的传感器件，以防止电极间短路。
相关文章
- 详细阅读
-
液压传动的工作原理详细阅读
液压传动的工作原理可以用一个液压千斤顶的动作来说明。图1-1 液压千斤顶工作原理图1—杠杆手柄 2—小液压缸 3—小活塞 4、7—单向阀 5—吸油管 6、10—管道 8—大活塞 9—大液压缸 11—截止阀 12—油箱图1-1所示为液压千斤顶的工作原理图。通过对上面液压千斤顶工作过程的分析，可以了解液压传动的基本工作原理。液压传动是利用有压力的油液作为传递动力的工作介质。......
2025-09-29
-
多CPU系统的工作原理详细阅读
在多CPU系统中，多CPU控制各自的相应模块，互相之间需要进行信息的交换。图10-5 多CPU系统的自动刷新原理假设系统的CPU1在B0～B1F之间设定了32点的自动刷新，CPU2在B20～B3F之间执行32点的自动刷新，如图10-6所示。图10-6 多CPU设置那么在CPU1的END处理期间，执行的处理过程为图10-5中的1.和4.，即：1）CPU1的B0～B1F传输软元件数据被传送到CPU1的自动刷新区（1.）。图10-7 多CPU系统FROM/TO指令图10-7表述的意思如下：1）用TO指令写入数据到PLC1的用户区（1.）。......
2025-09-29
-
PLC的工作原理简介详细阅读
PLC采用循环执行用户程序的方式，称为循环扫描工作方式，其运行模式下的扫描过程如图3-1所示。输出刷新阶段在执行完用户所有程序后，PLC将输出映像区中的内容送到寄存输出状态的输出锁存器中，这一过程称为输出刷新。PLC仅在扫描周期的起始时段读取外部输入状态，该时段相对较短，抗输入信号串入的干扰极为有利。图3-1所示工作过程是简化的过程，实际的PLC工作流程还要复杂些。......
2025-09-29
-
收音对讲机的工作原理解析详细阅读
TDA2822M的功能框图如图8.4-4所示，一般采用DIP8封装或SOP8封装，该收音对讲机使用的是SOP8封装。图8.4-10电感线圈8.电感线圈如图8.4-10所示，该收音对讲机使用了4个Φ3mm的电感线圈，L2的电感量为6T，L1、L3、L4的电感量都为5T。......
2025-09-29
-
高温电子消毒柜的工作原理详细阅读
高温型电子消毒柜是以远红外线电热元件为热源。远红外线有显著的加热效应和强烈的穿透能力，易被物体所吸收，因此被加热物体温度上升快，节约能量，达到高温杀菌、消毒的目的。此时220V交流电通过K2-2，使远红外线电热元件E1、E2通电加热，处于全功率工作状态，消毒柜温度可以一直上升到预定的温度125℃。当温度上升超过60℃时，作为控制温度的t2℃双金属片断开。图4-4 高温电子消毒柜电气原理图......
2025-09-29
-
催化剂的工作原理和应用详细阅读
原则上，好的催化剂在参与的反应过程中不会消耗，或者在直接参与反应后被释放出来，或者作为反应物的吸附剂，降低反应物的化学势。因此，化学反应只需要很少量的催化剂，以至于通常将贵金属与其他便宜的化合物制成合金。催化剂的一个缺点是相对脆弱。当有反应物侵蚀或者反应物中出现杂质时，都可能使催化剂发生改变或被惰化，我们称为中毒。......
2025-09-29
-
传真机的工作原理详解详细阅读
如图8-1所示，传真机的基本工作原理可以归纳为5个环节：发送扫描、光电转换、传真信号的调制/解调、记录转换、接收扫描。图8-1 传真机的基本工作原理发送扫描发送扫描是对发送图像进行从左到右、从上到下的扫描，把发送图像分解成许多微小像素，从而把二维图像信息转换成一维时间序列信号。......
2025-09-29
相关推荐