1）对于液压系统及液压元件的数学模型用模块式建模法建立后，在呈隐式状态方程组中，令其导数项为零得静态方程，该方程一般为非线性代数方程组，这时采用牛顿-拉夫逊方法作为解法基础。5）经算法对比验证表明，在动态方程呈线性时，用代数解法与传统Runge-Kutta法相比，其精度可在10-6以上或更高。15）常系数微分方程初值问题的代数解法可以作为标准算法之一采用。......
2023-06-22
直接代数解法中的方程病态问题（Stiffness）的解决方法
【摘要】：但是实际上，在运用直接代数解法时还需解决其带来的一些技术问题与相应的处理。首先是Stiffness问题即病态、刚性、坏条件或具有差别大的Lipsihitz问题。在液压系统特别是元件仿真中，多数场合会遇到病态问题。因此在模块式建模法的直接代数解法中，为了建立稳定的数值计算方法，着眼点是在保证精度的前提下，尽可能扩大稳定区域，使步长选择尽可能大，以达到仿真时间短，巨稳定、可靠、精度足够高的目的。
由参考文献[1]可知，本方法经理论论证、不同软件包的仿真结果对比及实例仿真与实验验证三个方面证实，直接代数解法的设想是正确可行的，并巨在建立的PERSIM软件包的实际应用中与已有的液压软件包的计算结果并无二致。但是实际上，在运用直接代数解法时还需解决其带来的一些技术问题与相应的处理。
首先是Stiffness问题即病态、刚性、坏条件或具有差别大的Lipsihitz问题。具体到液压模块式建模法中即为状态变量质量、液容和液感等中存在小参数，就会导致方程组病态：
其中e是与其他参数有数量级差别的小参数，会造成方程的Jacobi矩阵具有数量级相差很大的特征值负实部。
在液压系统特别是元件仿真中，多数场合会遇到病态问题。解决病态方程的关键是寻求适应性强的数值解法，寻求稳定域在负方向延续无穷的方法。
本方法研究表明，根据直接代数解法原理及实现途径，对于某些病态系统可直接调用标准的四阶Runge-Kutta法可以得到满意的结果，但有时会要求积分步长很小，造成仿真时间很长。加上还要根据计算精度选择步长，当病态严重时会造成坏解，甚至不收敛。因此在模块式建模法的直接代数解法中，为了建立稳定的数值计算方法，着眼点是在保证精度的前提下，尽可能扩大稳定区域，使步长选择尽可能大，以达到仿真时间短，巨稳定、可靠、精度足够高的目的。为此针对模块式建模法的隐式微分方程组，采用数值迭代公式，构造在m阶显式Runge-Kutta型公式中引人稳定参数s和a的数值方法。此时m阶显式Runge-Kutta型公式是：
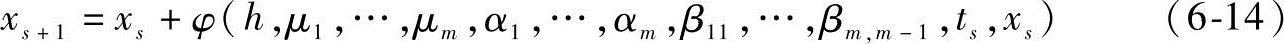
其构造的公式如下：
xs+1=αxs+sxs-1+φ （6-15）
按照s对稳定区域的影响，经研究应选取参数s接近于1原则，这样由于衰减特别快，计算量小，仿真时间短，精度高。但要注意，在具有高频振荡的系统不宜采用此方法，此时的积分步长要有一定限定，这可在软件中考虑到。
经PERSIM软件包仿真的经验证明，对于液压系统与元件的仿真，其步长在10-6为宜。在非病态方程的情况下10-4的步长也能成功，加速仿真使仿真时间极短。
有关液压螺纹插装阀技术与应用的文章
- 详细阅读
-
高等代数中的齐次线性方程组详细阅读
形如的一组线性方程称为n元齐次线性方程组.其中，矩阵称为齐次线性方程组的系数矩阵.记x=（x1，x2，…，xn）T，则这个齐次线性方程组可以简单地记作Ax=0.显然，齐次线性方程组必然有一组解x=（0，0，…，bn）.如果线性方程组Ax=0......
2023-11-22
-
线性代数习题解法+例题讲解详细阅读
，s）均可逆，则A可逆，且见例3.16.例3.12 已知，写出A可逆的一个充要条件，当A可逆时，求A－1.A可逆故当ad－bc≠0时，例3.13 设n阶方阵A 满足A3－2A2＋3A－4E＝O，则A－1＝________.若能找到n阶方阵B，使得AB＝E，则A－1＝B.这样的B应利用题设条件去找.应填由题设条件A3－2A2＋3A－4E＝O，移项得A3－2A2＋3A＝4E，左端提出公因子，得 A＝4E，即故知A可逆，且类似本题的一般问法：设f是多项式，且f＝akxk＋ak－1xk－1＋…......
2023-11-21
-
线性代数求解方程组的公共解与同解问题详细阅读
求两个方程组的公共解.①齐次线性方程组Am×nx＝0和Bm×nx＝0的公共解是满足方程组的解，即联立求解.同理，可求Ax＝α与Bx＝β的公共解.这里对读者的计算能力提出较高要求，但理论上没有什么难点.②求出Am×nx＝0的通解k1ξ1＋k2ξ2＋…......
2023-11-21
-
直接建立基本方程的平衡条件详细阅读
前面介绍了利用位移法基本结构来建立位移法方程。位移法典型方程实质上代表了原结构的结点和截面的平衡条件。因此，位移法方程的建立可以不通过附加约束的基本结构，而是利用杆件的物理方程［式（7-1）至式（7-4）］，直接取结点和截面一侧为隔离体的平衡条件，来建立以结点位移为未知量的位移法方程。利用等截面直杆的物理方程式（7-1）、式（7-2）及表 7-1，由跨度 l＝12 m，高 h＝6 m，可得图7-16建立位移法方程。......
2023-08-30
-
大学学习中的问题与解决方法详细阅读
3．学习动力不足学习动力不足是大学生学习中存在的普遍性问题。2．良好的大学学习习惯常规教学是以教师讲授为主的课堂教学。与教师、同伴共同探讨学习方法、交换学习材料、交流学习经验体会，并在必要的情况下接受他人的帮助。协作学习要求学习者主动地寻求学习伙伴并共同探索问题。学习者根据各自的兴趣、爱好及特长，组成2～6人的小组，确定学习任务，建立协作学习情境，引发积极的学习状态。......
2023-08-28
-
第四章：解密代数中的代问题详细阅读
）这里，摩斯沃斯认为代数只是“一堆杂乱无章的字母”而已，这种认知让我感到哀伤。我们今天所知道的“代数”概念直到十六世纪才完全形成。比如，摩斯沃斯就用下列式子：摩斯沃斯认为困难的方程作为一个例子来展示代数方程能使“任何人窒息”。他们的目的是将几何问题变为代数问题，或者将代数问题变成几何问题。做这一切的主要原因是一个代数方程可以被表示为一条曲线，或者一条曲线也可以被写作一个代数方程。......
2023-10-26
- 详细阅读
相关推荐