4.风电场对方向保护影响仿真根据对风电机组暂态电压、电流特性的分析结果，经过不同类型故障仿真计算，传统提取工频分量的傅里叶滤波算法得到的相位结果误差很大，对基于电压、电流相位关系方向元件的动作特性影响十分严重[4]。......
2023-06-28
经典算例展示与分享
【摘要】：图9.9弹靶侵彻过程提取弹丸的速度-时间曲线，如图9.10所示。采用cm-g-μs单位制。有限元模型如图9.12所示。表9.1常见炸药的JWL参数所需拼接盖板长度L=l+13mm=mm=580.12mm，取580mm。
9.2.3.1 弹靶侵彻
1. 问题描述
一个半径为4 cm、长为20 cm的圆柱形金属弹丸，以800 m/s的速度垂直撞击尺寸为64 cm×64 cm×3 cm的金属靶板。弹丸与靶板材料均为钢，计算弹丸贯穿靶板的变形过程，分析弹丸和靶板的破坏形态。
2. 物理建模
弹靶侵彻是典型的侵彻碰撞问题，弹丸初始速度较高，属于高速撞击范围。弹丸尺寸与靶板相比要小得多，靶板远端受到的弹丸作用很小，可认为靶板是无限域。由于弹靶侵彻的轴对称特性，并为减小计算量，利用LS-DYNA软件，采用1/2模型建模。计算模型使用三维实体Solid 164单元进行划分，靶板与弹丸直接作用区域网格加密。在对称界面上施加对称约束，弹丸和靶板之间采用侵蚀接触算法，在靶板边界处施加非反射边界，采用cm-g-μs单位制。
3. 材料参数
由于弹靶侵彻属于高速碰撞，在计算过程中会出现材料大变形问题，由于Johnson-Cook模型能够很好地描述金属材料（介质）在大应变、高应变率和高静水压力下的动态力学行为，因此在金属材料冲击爆炸问题的数值分析中得到广泛应用。
4. 结果分析
弹靶侵彻过程如图9.9所示。由图可知，弹丸与靶板在接触位置形成冲击波，并向外传播。在侵彻过程中，弹丸头部发生墩粗变形，靶板穿孔背部出现凸起。
图9.9 弹靶侵彻过程
提取弹丸的速度-时间曲线，如图9.10所示。由图可知，在撞击发生瞬间，弹丸速度迅速下降，之后，在穿孔过程中，速度下降趋势开始减缓，当完全贯穿后，弹丸速度保持不变，剩余速度约为600 m/s。
9.2.3.2 炸药的破坏效应
1. 问题描述
一个半径为2 cm、长为10 cm的圆柱形装药，底部放有一个半径为5 cm、厚为2 cm的钢板，装药与钢板中心轴重合，如图9.11所示。装药在顶部中心处起爆，观测钢板的变形过程，分析其破坏形态。
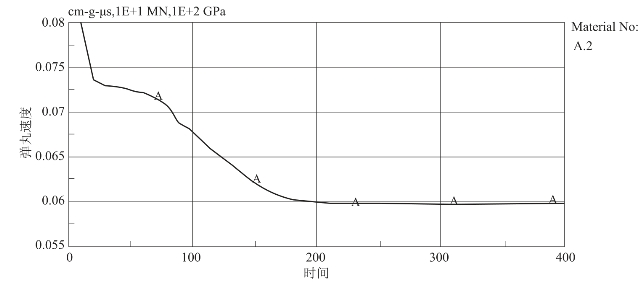
图9.10 弹丸的剩余速度曲线
2. 物理建模
数值模型由炸药、空气和钢板三部分组成，其中炸药和空气两种材料采用欧拉网格建模，为Solid 164单元，使用多物质ALE算法；钢珠采用拉格朗日网格建模，与空气和炸药材料间采用耦合算法。由于结构的对称性，为提高计算效率，建立1/4模型，在对称面施加对称边界，在空气域外侧施加无反射边界，模拟无限大空气域。采用cm-g-μs单位制。有限元模型如图9.12所示。
3. 材料参数
1）空气
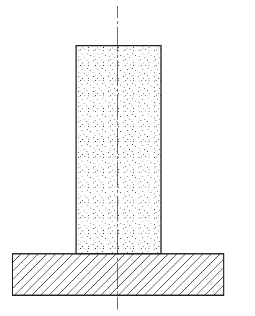
图9.11 装药破坏钢板的结构示意图
式中，γ为绝热指数，对于理想气体有γ=1.4；ρ为密度，空气的初始密度为0.001 225 g/cm3；初始压力为一个标准大气压；Eg=2.068×10 - 5，是气体比内能。
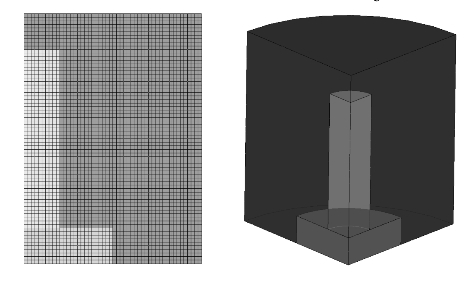
图9.12 有限元模型
2）装药
爆轰产物JWL状态方程不显含化学反应，能够精确描述爆轰产物的等熵膨胀过程，其具体形式为
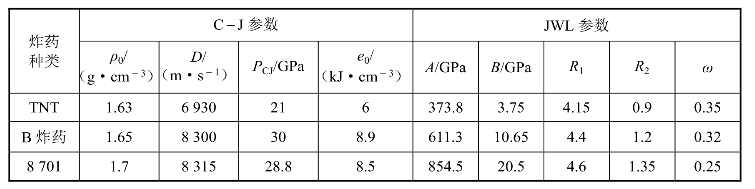
式中，P为爆轰产物的压力（Pa）；V为爆轰产物的相对比容，V=v/v0，量纲为1，v=1/ρ是爆轰产物的比容，v0是爆轰前炸药的初始比容；E为炸药比内能（J/m3）；A、B、C、R1、R2、ω为常数。常用炸药的JWL状态方程参数列于表9.1。
表9.1 常见炸药的JWL参数
3）钢板
在炸药爆轰作用于钢板时，主要有三个特征：高温、高压和高应变率。为准确描述钢板在此状态下的响应规律，采用Johnson-Cook模型描述。Johnson-Cook模型常用于模拟金属材料从低应变率到高应变率下的动态行为，该模型采用变量乘积关系描述了应变率、温度和应变的影响，本构方程如下：
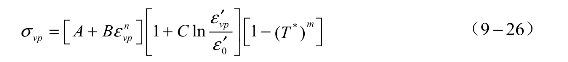
式中，σvp为von Miese流动应力；vpε为黏塑性应变；A为屈服强度；B为材料塑性硬化系数；C为黏塑性硬化指数；n为应变率敏感指数；
为真实黏塑性应变率；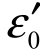
为参考应变率；m为温度软化指数；T*为量纲为1的温度，其计算公式为
式中，Tm为材料的熔点温度；Tr为参考温度，一般取为实验时室温；T为温度，单位采用国际制单位。表9.2所示为铸铝合金ZL114A的Johnson-Cook模型参数。
表9.2 钢珠的Johnson-Cook模型参数
4. 结果分析
装药爆轰及对钢板的作用过程如图9.13所示。由图可知，装药起爆后形成爆轰波向前传播，冲击波传播到钢板后，在钢板中传播振荡，且钢板在高温高压的爆轰产物作用下，逐渐发生凹陷，同时在背面形式凸起，如图9.14所示。
图9.13 装药爆轰及对钢板的作用过程
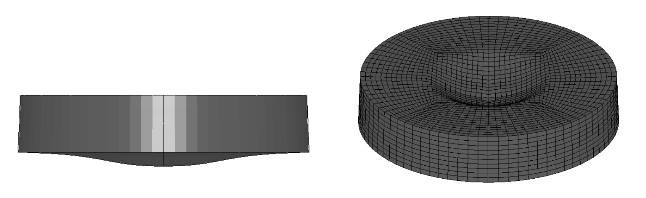
图9.14 钢板的变形过程
有关含能元器件设计原理的文章
- 详细阅读
-
算例介绍及仿真分析详细阅读
图7-8 风向γ=3°时风电场等效模型3.风电场故障电流特征仿真t=4s时刻，在主变压器低压侧F1点发生三相金属性短路，故障持续时间为0.1s，故障后5ms风电机组投入Crowbar电路，故障前STH风电场输入风速为10m/s。动作电流与制动电流均不再恒定并叠加有其他频率分量，会发生大范围抖动。......
2023-06-28
-
桥梁可靠度分析算例：显式功能函数详细阅读
图3.10与图3.11中：Ng为种群代数，β′为适应度值，Nit为迭代次数。图3.9拟合的功能函数图3.10基于遗传算法的验算点迭代过程图3.11不同算法的可靠指标迭代过程表3.3算例1的可靠指标计算结果表3.3中，e表示算法的误差，Ns表示样本数量。......
2023-09-19
-
桥梁可靠度分析方法与应用-算例分析结果详细阅读
表2.1计算结果比较图2.4算例1迭代过程图2.5算例2迭代过程图中虚线为采用文献［10］的响应面法的迭代过程，实线为改进后的响应面法迭代过程。计算结果表明：算例1的一次二阶矩法结果与文献［13］同种方法给出的结果β＝2.3309，几乎相等；而算例2的一次二阶矩法计算结果不收敛无法得出结果。......
2023-09-19
-
四点弯曲梁损伤算例分析结果详细阅读
图6.4损伤跨尺度演化过程模拟得到梁的位移－荷载曲线由图6.4可见，梁的损伤跨尺度演化导致梁的破坏是一个典型的脆性断裂破坏。从位移－荷载曲线可以明显地区分出梁中的损伤演化经历在梁的变形上反映出来的线性阶段、强化阶段、跳回阶段以及尾部阶段。这说明了梁中部高应力区域的损伤跨尺度演化过程对梁在宏观尺度下响应的显著影响。图6.6损伤演化过程中梁中性轴的移动......
2023-08-26
-
交直流混合输电系统算例分析详细阅读
交流母线额定电压都为220 kV，直流系统为双桥结构、双极运行，即每个换流站有四个换流变压器。图3.2系统接线图逆变侧换流变压器的参数如下：换流变压器单极容量300 MV·A；变压器漏抗12%；变压器交流侧电压230 kV；直流侧电压96 kV，可计算得出Xci。图3.3潮流计算的收敛特性由图3.3可知，交替迭代计算5次后，交直流系统潮流计算收敛。......
2023-06-29
-
如何写教后记？52题样例与经验分享详细阅读
但即使是对这堂获奖课，我也进行了认真的反思，并认真写了教后记——应该说，这堂课有不少令我感到满意的地方，比如，面对陌生的学生如何寻找最佳教学切入点？我上面这篇“教后记”就写得有血有肉，比较具体。教后记不是为发表而写的文字，是为自己成长而对自己的激励与鼓劲。希望你能坚持写教后记。......
2023-10-21
-
结构力学：快速学会力法计算步骤及算例详细阅读
根据力法的基本原理，力法计算超静定结构的方法和步骤可归纳如下：确定超静定次数，并选取适当的基本结构。应当注意的是，在选取基本结构时，若解除多余约束的方案不同，则将会得到不同形式的基本结构，虽然其力法典型方程的基本形式相同，超静定结构的求解步骤和最终结果亦相同，但计算工作量可能会有很大的差异。以下分别举例说明用力法计算各类超静定结构的具体计算方法。......
2023-08-30
相关推荐