由R13、R24、IC2及IC3组成恒压控制电路。反之输出电压下降,这样使输出电压稳定,起到稳压作用。由R13、R9、R21、IC2、IC3组成电流控制电路。由VD4整流、C17滤波的直流电压经R9限流供给IC2,没有上面介绍的电路供给IC3的效果好。图1-16 恒流恒压电路......
2023-06-25
通过大量的实验分析(见图3.17(b))可知,当SCB临界爆发时,恰好达到熔化状态,所以桥的熔点Tmelt可作为临界爆发点。
由于硅的熔点为1 684 K,高于电阻温度转折点Tt,所以可以将式(3-29)中接近液态时固态电阻代入式(3-34),可得临界爆发电流Iec表达式为
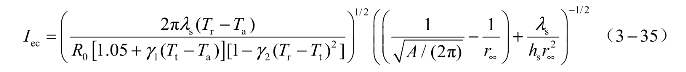
由式(3-35)可知,SCB的临界爆发电流主要受电阻、桥面积和塞子半径影响。临界爆发电流与SCB电阻的平方根成反比,与面积的1/4次方近似成正比。因为陶瓷塞的体积远远大于SCB的体积,所以计算临界爆发电流时取陶瓷的导热系数。陶瓷的物化参数[19]如表3.14所示。
表3.14 陶瓷的物化参数

例3.2 求解例3.1中的半导体桥换能元的临界爆发电流,其中基体为圆柱形陶瓷,基体直径为4.4 mm。
解:由式(3-24)可知,临界爆发电流的计算公式为
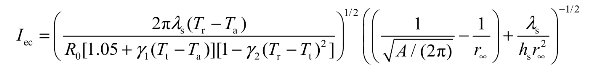
由例3.1知换能元的初始电阻R0 = 3.72 Ω,Tt = 1 510 K,r∞ = 4.4/2 = 2.2 mm,面积

基体为陶瓷材料,所以基体的参数可以取表3.14中的数据,将上述已知参数代入临界爆发电流的表达式中
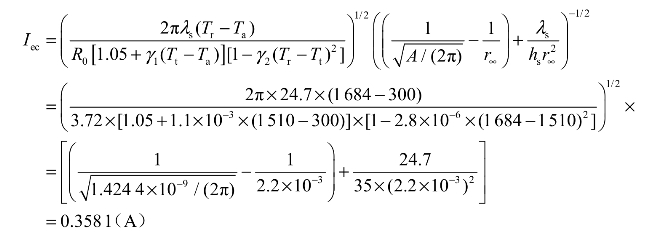
3.3.3.2 电容放电激励
1. 基本假设
在电容放电激励下,SCB换能机理属于电爆等离子体换能,即凝聚态SCB桥膜产生的焦耳热,加热半导体材料至汽化温度以上,使半导体材料汽化并电离,产生等离子体。为了使研究问题简化,需做如下假设:① 由于电容放电速度极快,桥膜产生的热量全部以热传导的方式沿垂直于桥面的方向传递给衬底和塞子,忽略向空气的散热;② 将桥膜、衬底和塞子看作物化性质相同的一体,称为桥—塞系统,响应过程中,导热系数、密度、比热容为恒值;③ 将桥膜看作桥—塞系统的一个发热边界,并且将桥—塞系统看作半无限厚平板;④ 忽略相变所吸收的能量;⑤ 响应过程中,SCB电阻看作恒值。
模型简化后的桥—塞系统物理图像如图3.26所示。
2. 数学方程
基于以上假设,桥—塞系统的导热可归结为一维平板无内热源非稳态导热问题,且具有第二类边界条件。选取桥的中心为坐标原点,垂直桥面的方向为x轴建立直角坐标系,桥—塞系统的导热微分方程和定解条件可描述为
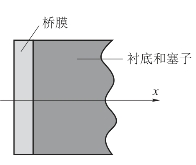
图3.26 SCB-塞子系统

式中,ks为SCB的热扩散率,ks=λs/(ρscs ),ρs为SCB密度(kg/m3),λs为SCB导热系数(W/(m·K)),cs为SCB的比热容(J/(kg·K));A为SCB的面积(m2),
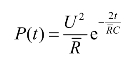 ,
, 为SCB响应过程中的时间平均电阻,
为SCB响应过程中的时间平均电阻, =
= (Rmin,Rmax )。
(Rmin,Rmax )。
根据式(3-36)可知

式(3-25)称为SCB的换能模型,第一个表达式为温度控制方程,表示内部温度的变化;第二个表达式为初始条件,表示加热的初始时刻,系统保持环境温度;第三个表达式为边界条件,表示传入系统界面的热量等于桥膜产生的焦耳热。导热微分方程具备了定解条件,可以求出该导热问题唯一的确定解。
3. 理论求解
利用拉氏变换法[26]对方程组(3-25)进行求解。令θs=Ts-Ta,桥塞的导热微分方程和定解条件式(3-36)可表示为

对桥塞导热微分方程(3-38)中的变量t取拉氏变换,记
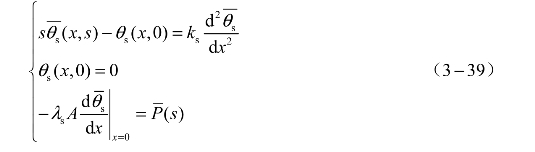
解方程得塞子温度响应方程的拉氏变换可表示为
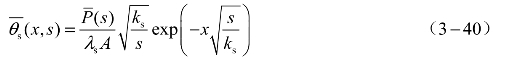
令 ,分别对
,分别对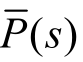 、F(s)取拉氏逆变换,由拉氏变换表知
、F(s)取拉氏逆变换,由拉氏变换表知

利用卷积定理可得
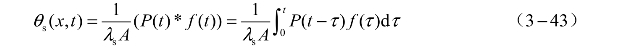
或
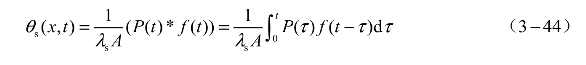
将式(3-30)、式(3-31)代入式(3-32)得
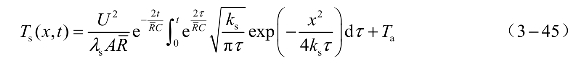
取x = 0代入式(3-34)可得桥塞系统边界(桥膜)的温度变化为

对式(3-46)中的![]() 在τ=0点进行泰勒级数展开,取一次项,简化后进行积分得SCB桥膜的温度变化表达式为
在τ=0点进行泰勒级数展开,取一次项,简化后进行积分得SCB桥膜的温度变化表达式为
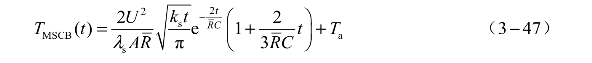
根据实验现象中临界爆发电压时固态温升阶段和液态温升阶段的持续时间,取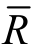 =0.15Rmax+0.85Rmin 。因为电容放电激励是一个强瞬态过程,热量主要在衬底内传递,塞子对作用过程的影响较小,所以计算时取多晶硅的物化参数[19],如表3.15所示。将l = 20.5 μm,w = 70.5 μm,θ = 40°,R0 = 3.88 Ω做基准计算,由式(3-24)得R=1.69Ω。放电电容选用10 μF,根据式(3-36)计算得不同激励电压时SCB桥面温度随时间的变化规律如图3.27所示。由图可知,SCB的温度先急剧上升,达到最大值后呈现缓慢下降的趋势,最终恢复环境温度,达到最高温度所用的时间与激励电压无关。
=0.15Rmax+0.85Rmin 。因为电容放电激励是一个强瞬态过程,热量主要在衬底内传递,塞子对作用过程的影响较小,所以计算时取多晶硅的物化参数[19],如表3.15所示。将l = 20.5 μm,w = 70.5 μm,θ = 40°,R0 = 3.88 Ω做基准计算,由式(3-24)得R=1.69Ω。放电电容选用10 μF,根据式(3-36)计算得不同激励电压时SCB桥面温度随时间的变化规律如图3.27所示。由图可知,SCB的温度先急剧上升,达到最大值后呈现缓慢下降的趋势,最终恢复环境温度,达到最高温度所用的时间与激励电压无关。
表3.15 硅的物化参数

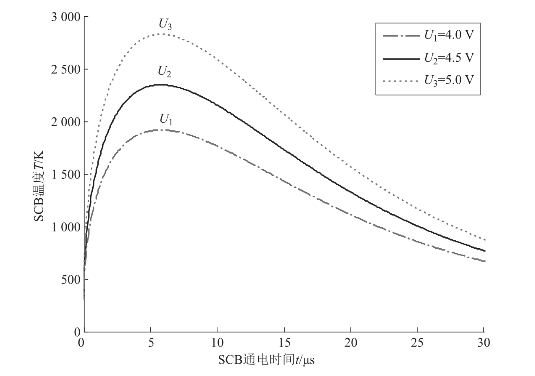
图3.27 SCB温度随时间的变化规律
令式(3-47)关于t的导数为零,可得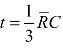 ,代入式(3-46)得SCB可达到的最高温度为
,代入式(3-46)得SCB可达到的最高温度为
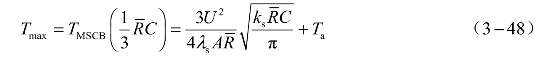
定义![]() 为加热时间常数,在加热时间常数之内,若SCB的最高温度低于其爆发点,不能爆发,若
为加热时间常数,在加热时间常数之内,若SCB的最高温度低于其爆发点,不能爆发,若![]() 时SCB的温度恰好升至其爆发点,则可以爆发。将SCB的爆发点Tr代入式(3-48)可得临界爆发电压表达式:
时SCB的温度恰好升至其爆发点,则可以爆发。将SCB的爆发点Tr代入式(3-48)可得临界爆发电压表达式:

由式(3-49)可知,临界爆发电压分别与SCB面积的平方根和阻值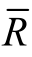 的1/4次方成正比。
的1/4次方成正比。
有关含能元器件设计原理的文章

由R13、R24、IC2及IC3组成恒压控制电路。反之输出电压下降,这样使输出电压稳定,起到稳压作用。由R13、R9、R21、IC2、IC3组成电流控制电路。由VD4整流、C17滤波的直流电压经R9限流供给IC2,没有上面介绍的电路供给IC3的效果好。图1-16 恒流恒压电路......
2023-06-25

VT1、VT2由两只不同型号的晶体管进行恒流控制。IC1电子开关既可以工作在2.2A受控恒压方式,也可工作在7.5V恒压状态下。当Vo≤2V时,VT1、VT2无工作电流,此时电流控制电路不起作用,但一次电流受IC1的电流限制,电流在R4上的压降VR4上升,VT2集电极电流下降,使光耦合器的工作电流迅速减小,迫使IC1进入重新启动状态。就是说,一旦电流控制电路失去控制,电路立即从恒流模式转入恒压状态,将Io拉下来,对IC1起到保护作用。......
2023-06-25

本章上述讨论所采用的时间都是以太阳时为计时系统的。本节将简单地叙述一下太阳时与钟时的关系及其相互换算。而太阳距天顶较近的一次“中天”称为“上中天”。将太阳视圆面中心连续两次“上中天”的时间间隔定义为一个“真太阳日”。这一时间系统,称为“真太阳时”,或简称为“太阳时”。地球每天自转一周,记为24个太阳时。平太阳连续两次上中天的时间间隔,称为“平太阳日”,1个平太阳日分为24个平太阳时。......
2023-06-23

图4-9多档恒流充电机线路工作原理:由电容C1~C4和开关S1~S4等组成电流选择电路,以选择合适的充电电流。该线路具有电流自动调整装置,能保证恒流充电;具有反向保护装置,蓄电池极性接反时不会被烧坏;具有蓄电池充足后能自动切断电源停止充电。图4-10晶闸管自动恒流充电机线路工作原理:单相交流电源经变压器T降压、二极管VD1、VD2全波整流,整流输出电压经晶闸管V调压送到蓄电池组。......
2023-06-20

作为教师,激情满满地上一堂、一天的课是容易做到的,难以做到的是天天、年年都激情四射地上好每一堂课,而且是重复的,熟悉的。朱永新老师说的教师应有“三历”,其中的“经历”我认为也是增加教学激情的主要方式。同样做教师也要有激情,有激情的教师感染学生,激励自己;没有激情的教师死气沉沉,课堂枯燥乏味,教出来的学生缺少血肉。......
2023-08-02

结构不完善的激励机制可能会无意间影响到整个网络的绩效。建立激励机制应遵循一定的原则。首先,为了防止搭便车的行为存在,激励机制应该与结果而不是与供给主体的活动挂钩。有效的激励机制还能避免供给主体的“扒皮”行为。扒皮行为是指供给主体快速抽取最容易办理的案件,而将难度大的案件留给其他伙伴去处理。[58]总之,完善的激励机制能够带来较高的合作供给的绩效。......
2023-06-27

选取系统的供电可靠性为约束条件。即约束条件为:g=LPSP,取约束函数的宽容系数ε1=LPSPreq;g=ΔE,取约束函数的宽容系数ε2=ΔEreq;g=n,取约束函数的宽容系数ε3=nreq。......
2023-06-23

装置进入充电恒流模式时,通过矩阵键盘进行充电电流设置,单片机通过DA设置恒流模块,通过ADC1和ADC2采集并显示相应电流电压值,并判断电压以确定是否启动过充保护。系统采用了具有高处理速度,低功耗的STM32单片机。图A-2-1系统总体框图考虑重量、效率要求,主要功率电路采用单片集成方案。综合考虑采用方案2。......
2023-06-23
相关推荐