在原来的正立投影面、水平投影面、侧立投影面三个基本投影面的基础上，增加了分别与它们平行的三个基本投影面，构成六面体方箱，将物体围在其中，这六面体的六个面均为基本投影面。各投影面展开时，规定正立投影面不动，其余各投影面按图6-1所示的方向，展开到与正立投影面在同一个平面上。图6-2六个基本视图的配置对于同一物体，并非要同时选用六个基本视图，至于选取哪几个视图，要根据物体的复杂程度和结构特点而定。......
2023-06-28
基本视图及展开投影图
【摘要】：如图9-1所示，在水平投影对面增加投影面H1，其上投影称为底面图；在正立投影面对面增加的投影面用V1表示，其上投影图称为背立面图；在左侧立面对面增加的投影面用W1表示，其上的投影图称为右立面图。得到的6个视图称为基本视图。图9-16个基本视图的立体图各视图的位置也可按主次关系从左至右依次排列，如图9-4所示。图9-26个基本视图的展开图9-36个基本视图的展开后的投影图9-46个基本视图按主次关系排列
三面投影体系是由水平投影面、正立投影面和侧立投影面组成，所作形体的投影图分别是水平投影、正立投影图和侧立投影图，在工程图中分别称为平面图、正立图和侧立面图。
在很多情况下，仅采用三视图难以表达清楚整个形体，例如一个建筑物，通常其正面和背面是不同的。因此，有必要将三视图进行增加到6个方向进行投影，从而形成6个视图。如图9-1所示，在水平投影对面增加投影面H1，其上投影称为底面图；在正立投影面对面增加的投影面用V1表示，其上投影图称为背立面图；在左侧立面对面增加的投影面用W1表示，其上的投影图称为右立面图。
得到的6个视图称为基本视图。基本视图所在的投影面称为基本投影面，将6个基本视图展开，如图9-2所示。
6个视图展开后的排列位置如图9-3所示。在这种情况下，为合理利用图纸，可以不注视图名称。
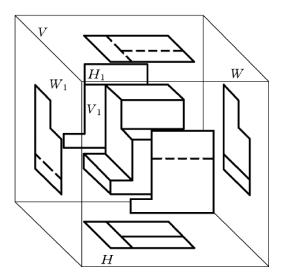
图9-1 6个基本视图的立体图
各视图的位置也可按主次关系从左至右依次排列，如图9-4所示。但在这种情况下，必须注写视图名称。视图名称注写在图的下方为宜，并在名称下划一粗横线，其长度应以视图名称所占长度为准。
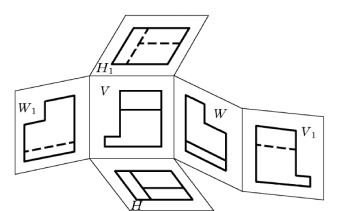
图9-2 6个基本视图的展开
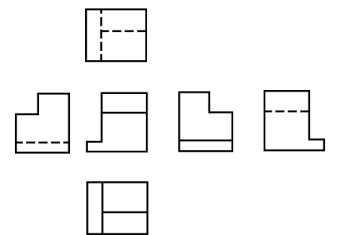
图9-3 6个基本视图的展开后的投影
图9-4 6个基本视图按主次关系排列
有关建筑工程制图的文章
- 详细阅读
-
创建基本视图操作步骤及对话框解读详细阅读
下面创建图8.4.1所示的基本视图，操作过程如下：Step1.打开零件模型。图8.4.1零件的基本视图图8.4.2零件模型Step2.进入制图环境。Step4.定义基本视图参数。图8.4.3“图纸页”对话框图8.4.4“基本视图”对话框图8.4.4所示的“基本视图”对话框中的按钮说明如下：●区域：该区域用于加载部件、显示已加载部件和最近访问的部件。选择下拉菜单命令，系统弹出“基本视图”对话框。......
2023-11-23
-
绘制透视图的基本术语详细阅读
透视图的绘制中包括的基本术语，如图6-2所示。基面是指放置物体的水平面。视高是指人的眼睛到站立点的高度，也就是视点S和站点s之间的距离，即高度Ss。主视线（Ss′）。以后凡几何形体的透视，均用与表示几何形体体身相同的字母或数字，在左上角加“0”表示。次透视是指基点a的透视，即视线Sa与画面V 的交点，之所以称为次透视是相对于空间点A而言的。连系线是指点的透视A0与次透视 的连线。......
2023-06-22
-
表面展开图的基本原理与方法详细阅读
本章的地位及特点表面展开图是本课程的补充内容，是工程中制作毛坯为金属板的零件时常用的图样，在今后的学习和工作中使用率较高。本章主要介绍平面立体表面和可展曲面展开及不可展曲面近似展开的基本原理和方法。在实际生产中，绘制表面展开图时可采用图解法或计算法。图10-1物体的表面展开图10-2金属板制零件......
2023-06-28
-
UGNX10.0基本视图及零件模型新建工程图详细阅读
图12.4.1 零件的基本视图图12.4.2 零件模型新建工程图。选择下拉菜单命令，系统弹出“图纸页”对话框；在对话框中选择图12.4.3所示的选项，然后单击按钮，系统弹出图12.4.4所示的“基本视图”对话框。在图12.4.5所示的三个位置单击以生成主视图、左视图和俯视图。图12.4.4所示的“基本视图”对话框中的按钮说明如下。......
2023-10-17
-
n阶行列式展开规则及解析详细阅读
设n阶行列式则有Dn=ai1Ai1+ai2Ai2+…+anjAnj（Dn按第j列展开，j=1，2，…，n），其中，Aij是元素aij的代数余子式，即（-1）i+j与Dn中去掉第i行和第j列元素后的n-1阶行列式之积.注ak1Ai1+ak2Ai2+…，n，但k≠i），a1kA1j+a2kA2j+…......
2023-10-27
- 详细阅读
-
洛朗级数展开定理、复变函数及应用详细阅读
在圆环域R1 ＜|z-z0|＜R2内处处解析的函数f(z)可以展开成z-z0的正、负幂项都有的级数,称为f(z)的洛朗(Laurent) 级数.定理1(洛朗级数展开定理) 设R1 ＜|z - z0| ＜R2 为环域D,函数f(z)在D内解析,则对D 内任意点z有其中C为在该环域内任意一条围绕点z0的正向简单闭路.证明对任意z ∈D,在D内分别作正向圆周C1 和C2,其中C1为|ζ-z0|=r1,C......
2023-10-30
相关推荐