地面的等高线已经给出，根据已知的等高线和比例尺先求出平面上等高线的平距并作出坡面上的等高线。等高线34到35之间的交线需要采用内插法求解，即分别对平面和地形面上的等高线按间距加密，求出更多的交点，再完成连接。将直线的标高投影a21.5b23.5与各地形面上各等高线的交点按高程和水平距离点到平行线组中，连接各点得地形面截交线。图7-25求管线与地面的交线图7-25求管线与地面的交线......
2023-06-22
曲面与地形面的交线分析
【摘要】：求曲面与地形面的交线，即求曲面上与地形面上标高相同的等高线的交点，然后用平滑曲线顺次连接起来即得曲面与地面的交线。同理，由于填土部分的坡度为1∶1.5，故其平距为1.5个单位长度，据此便可作出填土部分平面坡面与坡面、坡面与地形面的两高程等高线的交点，顺次连接这些交点即得相邻边坡坡面的交线及各坡面与地形面的交线。根据填方和挖方的坡度算出同坡曲面上等高线的平距，作出同坡曲面上的等高线。
求曲面与地形面的交线，即求曲面上与地形面上标高相同的等高线的交点，然后用平滑曲线顺次连接起来即得曲面与地面的交线。
【例7-8】 如图7-26所示，要在山坡上修筑一带圆弧的水平广场，其标高为25m，填方边坡1∶1.5，挖方边坡1∶1，求其填挖边界线。
解：
（1）首先确定填挖分界线，水平广场高程为25，因此，将地面上标高为25的等高线作为填挖分界线。它与广场边缘的交点即为填挖分界点。
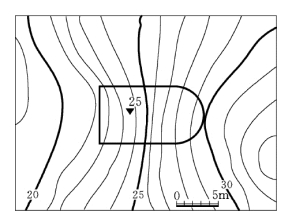
图7-26 求水平广场与地面的交线
（2）地形高程比25高的地方，应该是挖土的部分，在这些地方的坡面下降方向是朝着广场内部的，因而在圆弧形边缘处的坡面应该是倒锥面；而高程比25低的地方，应该是填土部分，在这些地方的坡面下降方向，应该是朝着广场外部的。
（3）由于挖方部分的坡度为1∶1，则平距为1∶1，故根据比例尺以1单位长度为间距，顺次作出挖土部分的两侧平面边坡坡面的等高线，并作出广场半圆边缘的半径长度加上整数倍的平距为半径的同心圆弧，即为倒圆锥面上的各等高线。
同理，由于填土部分的坡度为1∶1.5，故其平距为1.5个单位长度，据此便可作出填土部分平面坡面与坡面、坡面与地形面的两高程等高线的交点，顺次连接这些交点即得相邻边坡坡面的交线及各坡面与地形面的交线。
（4）在等高线18与19及33与34之间的交线，可用内插法确定。填方相邻两边坡的交线与地形面的交点。
（5）图中还画出方向和坡面等高线垂直，位置画在高处的均匀长短细线，即边坡示坡线，使由坡面和地形面的交线组成封闭的填挖边界线，如图7-27所示。
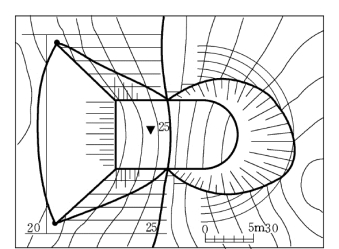
图7-27 求水平广场与地面的交线结果
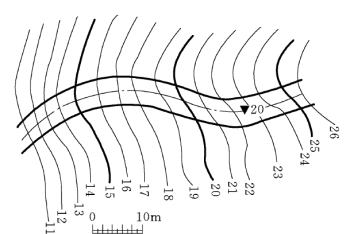
图7-28 弯道的已知条件
【例7-9】 如图7-28所示，在地面上修筑一条弯曲的道路，路面为平坡标高20m，道路两侧边坡，填方为1∶1.5，挖方为1∶1，求填挖边界线。
解：
（1）先找出填挖分界点，地形面上与路面上标高相同之点即为填挖分界点。因为道路标高为20m，故以地面上标高为20的等高线为填挖分界线。填挖分界点左面部分的地面标高比路面标高低，故为填方，填挖分界点右面部分的地面标高比路面高，故为挖方。
（2）各坡面为同坡曲面，同坡曲面上的等高线为曲线，在填方地段，愈往外的等高线，高程递减，即地势愈低；在挖方地段，愈往外的等高线，高程递增，即地势愈高。路缘曲线就是标高为20的等高线。
（3）根据填方和挖方的坡度算出同坡曲面上等高线的平距，作出同坡曲面上的等高线。由于路面标高都是20，就是平坡，所以无论是挖方地段还是填方地段，等高线与路缘曲线都是平行的。当路线为圆曲线时，可找出圆心，作等间距（平距）的同心圆，即得坡面上的等高线。
（4）连接坡面上各等高线与地面上同高程等高线的交点，即得填挖边界线，如图7-29所示。
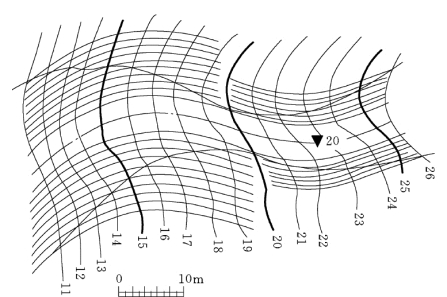
图7-29 求弯道的填挖边界线结果
有关建筑工程制图的文章
- 详细阅读
-
镜像曲面与合并曲面的创建方法与步骤详解详细阅读
在默认情况下，镜像曲面与原曲面具有从属关系，这种关系在做复杂曲面时显得特别重要。曲面合并是将已经创建的两个曲面通过合并处理合为一个曲面。由于曲面合并特殊的作用，使其在曲面设计中占据举足轻重的地位，尤其是在创建复杂曲面时，曲面合并更加行之有效，方便快捷。创建镜像与合并曲面的一般方法与步骤如下：打开源文件第7章│7-3.prt。5）运用同种方法合并其余曲面，创建如图7-55所示的合并曲面特征。......
2023-06-19
-
相切曲面的混合及其应用详细阅读
超出拔模曲面的恒定拔模角度进行相切拔模表示通过沿参照曲线的轨迹与拖动方向成指定角度而创建的相切曲面，它的适用范围是常规拔模无法比拟的。其具体步骤如下：打开源文件第5章∣5-6-2.prt，实例模型如图5-70所示。1）单击选项卡组中的选项，系统将弹出对话框。图5-72 选项栏图5-73 效果图注：使用曲线驱动拔模时，因其是双侧拔模，方向无影响；而使用外部混合拔模时，因其是单侧拔模，所以要慎重考虑方向的选择。......
2023-06-19
-
曲面体截交线-画法几何与土木工程制图详细阅读
曲面体的截交线一般情况下是平面曲线。当截平面与直纹曲面交于直素线，或与曲面体的平面部分相交时，截交线可为直线。因此求曲面体的截交线，实际上是作出曲面上的一系列的共有点，然后顺次连接成光滑的曲线。曲面体的投影轮廓线与截平面的交点，是截交线虚实线的分界点。3）球的截交线图6—12正平面与球相交无论截平面处于何种位置，它与球的截交线总是圆。例6—10求作铅垂面P与回转体的截交线。......
2023-09-24
-
如何实现曲面的延伸扩展？详细阅读
延伸曲面是将曲面沿着边界进行延伸以扩展曲面面积，并且延伸部分可以保持原状，也可以更改形状。延伸的方式有三种：延伸到平面、沿曲面延伸和多点延伸。图7-67 选项卡 ：测量参考曲面中的延伸距离，即沿曲面延伸的距离。......
2023-06-19
-
平面体与曲面体相交线详细阅读
平面体与曲面体的相贯线，一般情况下是由若干段平面曲线组成的，特殊情况下可包含直线段。因此，求平面体与曲面体的相贯线，可归结为求曲面体的截交线和求直线与曲面体的交点。例6—14如图6—19a所示，三棱柱与圆锥相贯，求作其相贯线。解由投影图可看出，三棱柱从前至后全部贯穿圆锥，形成前后对称的两组相贯线。图6—20圆锥的贯通孔判别相贯线的可见性。......
2023-09-24
-
球体截交线的探究详细阅读
前面已经讲过，所有过球心的直线均可视为球面的轴线，因此平面与球相交时，不论平面与球的相对位置如何，其截交线总是圆。两个侧平面P与半球的截交线，其侧面投影是半圆的一部分，水平投影积聚成直线；水平面Q截球体，其水平投影是圆的一部分，侧面投影积聚成直线；两平面P与Q的交线均为正垂线。表4-3球体的截交线图4-35开槽半球例4-17已知带切口球体的主、俯视图，完成其左视图。......
2023-06-28
-
点曲面铰的设置与多截面曲面的定义详细阅读
本节定义点曲面铰。点是笔零件笔尖上的点,曲面是17.1节生成的多截面曲面。本节没有对定义好的点曲面铰进行模拟运动分析。在对话框,更新了选项内容。图17-8 选择曲面作为,选择铅笔顶点作为总结：本章学习的是点曲面铰的设置。本章的新内容除定义点曲面铰外,还有定义多个参考平面,定义多截面曲面,特别是多截面曲面的定义,由于曲线草图的方向问题,肯定一次无法完成曲面的生成,要反复调整草图的方向。......
2023-07-01
相关推荐