首页理论教育平面与地形面的交线分析

平面与地形面的交线分析

2023-06-22 理论教育版权反馈

【摘要】：地面的等高线已经给出，根据已知的等高线和比例尺先求出平面上等高线的平距并作出坡面上的等高线。等高线34到35之间的交线需要采用内插法求解，即分别对平面和地形面上的等高线按间距加密，求出更多的交点，再完成连接。将直线的标高投影a21.5b23.5与各地形面上各等高线的交点按高程和水平距离点到平行线组中，连接各点得地形面截交线。图7-25求管线与地面的交线图7-25求管线与地面的交线

求平面与地形面的交线，即求平面上与地形面上标高相同的等高线的交点，然后用平滑曲线顺次连接起来即得交线。

【例7-6】　求图7-24中地面与坡度为2/3的坡面的交线。

pagenumber_ebook=120,pagenumber_book=108

图7-24　求平面与地面的交线

解：

（1）作平面的等高线。地面的等高线已经给出，根据已知的等高线和比例尺先求出平面上等高线的平距并作出坡面上的等高线。平面上等高线的平距

按照平面的倾斜方向和比例尺，作等高线36的平行线组（间距为1.5个单位），即得到平面上的等高线。

（2）作平面与地面的交线。平面上和地形面上标高相同的等高线的交点，即是所求的交线上的点。等高线34到35之间的交线需要采用内插法求解，即分别对平面和地形面上的等高线按间距加密，求出更多的交点，再完成连接。

【例7-7】　已知直管线两端的标高分别为21.5和23.5，求管线AB与地面的交线。

分析：利用前面学习过的地形断面图，假想用一个断面沿AB管线将地面截开，得到其地形断面图，作出假想平面与地形面的截交线，再求管线与截交线的交点，即可得到管线与地形面的交点。

解：

（1）根据比例尺作间距为1个单位的平行线组。

（2）将直线的标高投影a21.5b23.5与各地形面上各等高线的交点按高程和水平距离点到平行线组中，连接各点得地形面截交线。

（3）将直线的标高投影a21.5b23.5按其水平距离点到平行线组中，连接可得AB直线，AB直线与截交线的交点k1k2k3k4即是AB直线与地面的交点。

（4）将所求交点返回到标高投影中，并将地面以下的部分画成虚线，完成作图，如图7-25所示。

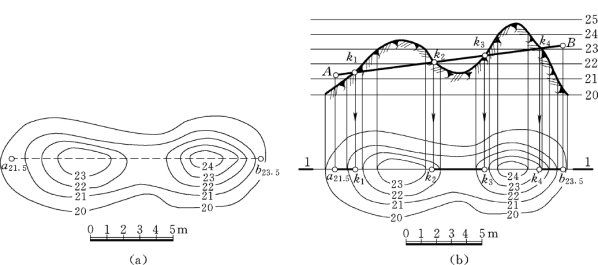
pagenumber_ebook=121,pagenumber_book=109

图7-25　求管线与地面的交线