首页理论教育同坡曲面标高投影技巧

同坡曲面标高投影技巧

2025-09-29 理论教育版权反馈

【摘要】：两个相切曲面与同一水平面的交线必然相切，即同坡曲面与运动正圆锥的同高程等高线必然相切。道路在弯道处，无论其路面有无纵坡，其边坡均为同坡曲面。图7-19求匝道与干道的标高投影图解：计算各边坡平距l=1/1=1单位。弯道处的两条路边线即为同坡曲面的导线，在导线上取其整数标高点作为锥顶位置。按照平面标高投影的方法作出同坡曲面与干道边坡的交线。

一个正圆锥沿一条空间曲导线运动且轴线方向保持不变，其包络曲面被称作同坡曲面，即各处坡度皆相等的曲面，如图7-18所示。

pagenumber_ebook=117,pagenumber_book=105

图7-18　同坡曲面

同坡曲面有如下特征。

（1）运动的正圆锥在任何位置都和同坡曲面相切，切线即为曲面在该处的最大坡度线，故曲面上各处坡度均等于运动正圆锥的坡度。

（2）两个相切曲面与同一水平面的交线必然相切，即同坡曲面与运动正圆锥的同高程等高线必然相切。

工程上常用到同坡曲面。道路在弯道处，无论其路面有无纵坡，其边坡均为同坡曲面。

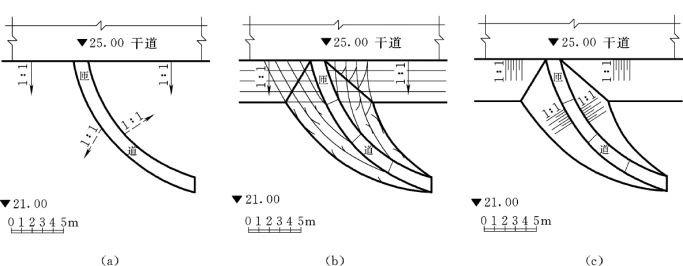
【例7-5】　如图7-19 （a）所示，一弯曲倾斜匝路与干道相连，干道顶面标高25.00m，地面标高21.00m，弯曲匝道由地面逐渐升高与干道连接，求其坡脚线和坡面交线。

pagenumber_ebook=117,pagenumber_book=105 (https://www.chuimin.cn)

图7-19　求匝道与干道的标高投影图

解：

（1）计算各边坡平距l=1/1=1单位。

（2）弯道处的两条路边线即为同坡曲面的导线，在导线上取其整数标高点作为锥顶位置。

（3）分别以这些整数标高点为圆心，R=1、2、3、4为半径作同心圆，即为各正圆锥的等高线，如图7-19 （b）所示。

（4）作正圆锥上同标高的等高线的曲切线（包络线），即得到匝道边坡的等高线。

（5）按照平面标高投影的方法作出同坡曲面与干道边坡的交线。

（6）将结果描深，画出示坡线，作图完成，如图7-19 （c）所示。