两个相切曲面与同一水平面的交线必然相切，即同坡曲面与运动正圆锥的同高程等高线必然相切。道路在弯道处，无论其路面有无纵坡，其边坡均为同坡曲面。图7-19求匝道与干道的标高投影图解：计算各边坡平距l=1/1=1单位。弯道处的两条路边线即为同坡曲面的导线，在导线上取其整数标高点作为锥顶位置。按照平面标高投影的方法作出同坡曲面与干道边坡的交线。......
2023-06-22
平面标高投影技巧
【摘要】：如由三点表示的平面，在标高投影中则为由三点的标高投影来表示。
7.2.3.1 平面上的等高线和坡度线
1.等高线和坡度线
标高投影中，预定高度的水平面与所表示表面（平面、曲面、地形面）的截交线称为等高线。如图7-7 （a）所示，平面上的水平线即平面上的等高线，也可看成是水平面与该平面的交线。在实际应用中常取整数标高的等高线，它们的高差一般取整数，如1m、5m等，并且把平面与基准面的交线，作为高程为零的等高线。图7-7 （b）为平面P上的等高线的标高投影。
从标高投影图中可以看出，平面上的等高线是一组互相平行的直线，当相邻等高线的高差相等时，其水平间距也相等，这是平面上的等高线特性。图7-7（b）中相邻等高线的高差为1m，它们之间的水平间距就是平距。
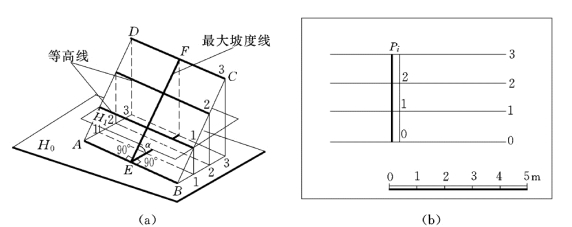
图7-7 平面上的等高线和坡度比例尺
平面的坡度线和平面上的水平线垂直，根据直角投影定理，它们的水平投影应互相垂直。坡度线的坡度就是该平面的坡度。
2.坡度比例尺
工程上有时也将坡度线的投影附以整数标高，并画成一粗一细的双线，称为平面的坡度比例尺，如图7-7 （b）所示。P平面的坡度比例尺用字母Pi表示。
7.2.3.2 平面的表示方法
在正投影中我们知道平面可以用几何元素、最大坡度线和迹线等方法表示，这些表示方法在标高投影中仍然适用，只是转换为用标高投影来表达。如由三点表示的平面，在标高投影中则为由三点的标高投影来表示。在标高投影中，平面常用如下方法表示。
1.等高线表示法
这种表示方法实质上是两平行直线表示平面，平面上的水平线称为平面上的等高线。在实际应用中我们一般采用高差相等，标高为整数的一系列等高线来表示平面，并把基准面H 的等高线，作为零标高的等高线，如图7-8所示。平面上的等高线是彼此平行的直线，当高差相同时，等高线间距相等。
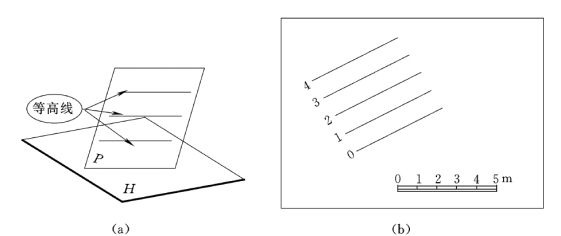
图7-8 平面的等高线表示法
2.坡度比例尺表示法
坡度比例尺表示法就其实质而言就是最大坡度线表示法。如图7-9 （a）所示，将平面上最大坡度线的投影附以整数标高，并画成一粗一细的双线称为平面的坡度比例尺。
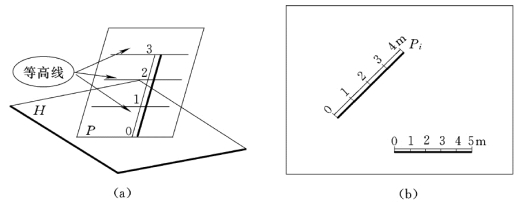
图7-9 平面的坡度比例尺表示法
已知平面的等高线组，可以利用等高线与坡度比例尺的相互垂直关系，作出平面上的坡度比例尺，反之亦然。
坡度比例尺已知，则平面对基准面的倾角可以利用直角三角形法求得。图7-9 （b）是根据P平面的等高线作出的坡度比例尺。
3.用平面上的一条等高线和平面的坡度表示平面
平面上的一条等高线已知，就可定出坡度线的方向，由于平面的坡度已知，该平面的方向和位置就确定了。如果作平面上的等高线，可利用坡度求得等高线的平距，然后作已知等高线的垂线，在垂线上按图中所给比例尺截取平距，再过各分点作已知等高线的平行线，即可作出平面上一系列等高线的标高投影，如图7-10所示。
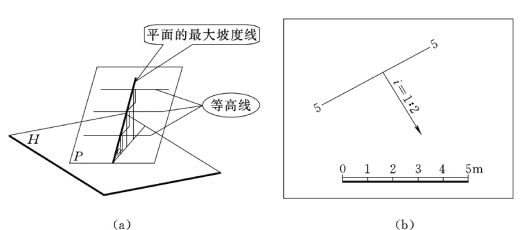
图7-10 用平面上的一条等高线和平面的坡度表示平面
4.用平面上的一条非等高线和该平面的坡度与倾向表示平面
图7-10为一标高为5m的水平场地及一坡度为1∶3的斜坡引道，斜坡引道两侧倾斜平面ABC和DEF 的坡度均为1∶2，这种倾斜平面可由平面内一条倾斜直线的标高投影加上该平面的坡度来表示，如图7-11所示。图中的箭头只是表明该平面向直线的某一侧倾斜，并代表平面的坡度线方向，坡度线的准确方向需作出平面上的等高线后才能确定，所以用虚线表示。
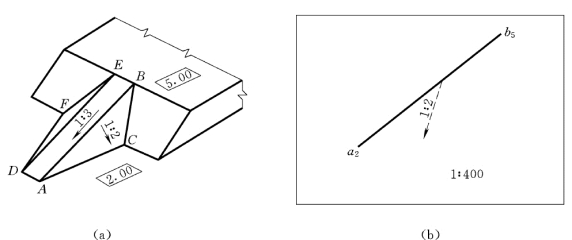
图7-11 用平面上的一条非等高线和该平面的坡度与倾向表示平面
7.2.3.3 两平面的相对位置
两平面在空间的相对位置可分为平行与相交两种情况。
1.平行
如果两平面平行，则它们的坡度比例尺和等高线互相平行，平距相等，标高数字的增减方向一致，如图7-12 （a）所示。
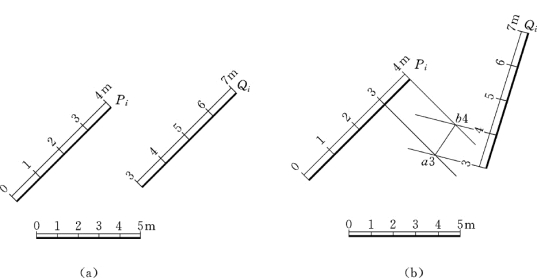
图7-12 两平面相对位置
（a）平行；（b）相交
2.相交
在标高投影中求两平面的交线，是利用辅助平面法在相交两平面上求得两共有点，其连线即为两平面的交线。通常采用水平而作为辅助面，如图7-12所示，水平辅助面与P、Q两平面的截交线是两条相同高程的等高线，这两条等高线的交点就是两平面的共有点，分别求出两个共有点并连接起来，就可求得交线。
【例7-2】 如图7-13所示，已知两平面P、Q，求它们的交线。
分析：两平面的交线为两平面上高程相同的等高线交点的连线。Q平面直接用等高线表示，而P平面已知一条等高线，再求一条等高线即可求出交线。
解：
（1）延长P平面上等高线5，与Q平面上等高线5相交，得交线上一点a5。
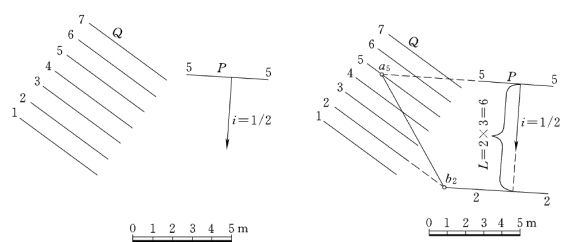
图7-13 求平面P、Q的交线
（2）利用已知P平面的坡度和比例尺求出P 平面上的另一等高线，并求出其与Q平面上同等高线的交点。
（3）连接a5、b5，得两平面的交线。
7.2.3.4 求坡面交线、坡脚线或开挖线
在工程中，把建筑物相邻两坡面的交线称为坡面交线，坡面与地面的交线称为坡脚线（填方）或开挖线（挖方）。
在工程中，坡面倾斜情况可用示坡线表示。如图7-14 （c）所示，图中长短相间的细实线叫示坡线，它与等高线垂直，用来表示坡面，短线画在高的一侧。
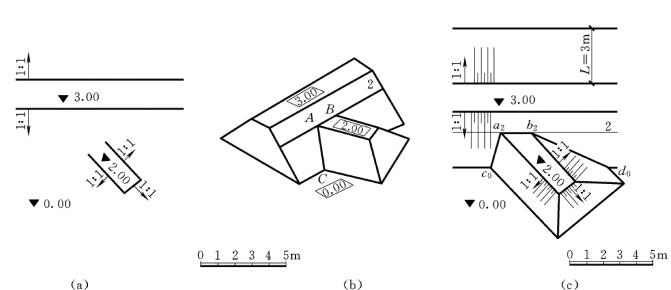
图7-14 求主堤与支堤相交的标高投影图
【例7-3】 已知主堤与支堤相交，顶面标高分别为3m和2m，地面标高为0，各坡面坡度如图7-13 （a）所示，求两堤相交的坡脚线和坡面交线。
解：
（1）求坡脚线。先求出主堤顶边缘到坡脚线的水平距离L=H/i= （3－0）/1=3m，再沿两侧坡面坡度线方向按所给比例尺量取，过零点作顶面边缘的平行线，即得两侧坡面的坡脚线。同理可作出支堤的坡脚线。
（2）求支堤顶面与主堤坡面的交线。支堤顶面标高为2m，与主堤坡面交线就是主堤坡面上标高为2m的等高线中的a2b2段。
（3）求主堤坡面与支堤坡面的交线。主堤与支堤的坡脚线交于c0、d0，连接c0、a2和d0、b2，即得主堤与支堤的坡面交线。
（4）描深坡脚线和坡面交线，画出各坡面的示坡线。
【例7-4】 如图7-15 （a）所示，一斜坡引道直通水平场地，设地面高程为2m，水平场地顶面高程为5m，求引道和水平场地的坡脚线和坡面交线。
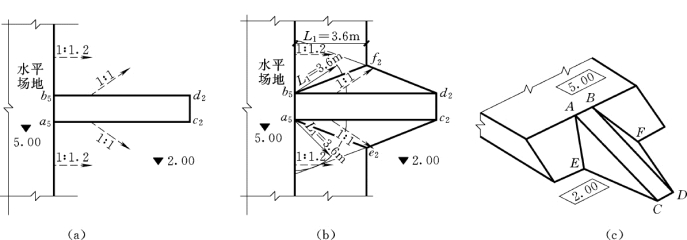
图7-15 求倾斜引道与水平场地的坡脚线和坡面交线
解：
（1）求坡脚线。水平场地边缘与坡脚线的水平距离根据已知坡度和高差可求得，即L1=1.2×3m=3.6m。利用比例尺可作出水平场地的坡脚线。由于引道是倾斜的，在求其坡脚线时，分别以a5和b5为圆心，以L2=1×3m=3m （根据比例尺量取）为半径画圆弧，再分别由c2和d2作两圆弧的切线，即得引道两侧的坡脚线，如图7-15 （b）所示。
（2）求坡面交线。水平场地与斜坡引道的坡脚线分别相交于e2和f2，连接a5e2和b5f2，即得到坡面交线。
（3）将所求得坡脚线和坡面交线描深，画出各坡面的示坡线，如图7-15 （c）所示。
有关建筑工程制图的文章
- 详细阅读
-
平面标高投影：画法几何及土木制图详细阅读
1）平面上的等高线和坡度线标高投影中，预定高度的水平面与所表示表面的截交线称为等高线。图9—6b为平面P上的一系列等高线的标高投影。2）平面的表示法在正投影中所介绍的用几何元素表示平面的方法在标高投影中仍然适用。但要注意的是，在用坡度比例尺表示平面时，标高投影的比例尺或比例要同时给出。图9—11作已知平面的等高线3）平面与平面的交线在标高投影中，求两平面的交线，通常采用水平面作为辅助面。......
2023-09-24
-
直线的标高投影解析详细阅读
图7-2直线的标高投影为了更好的了解这两种表示方法，我们先来关注以下两个问题。以直线的标高投影为一条直角边，另一条直角边为直线两端点的高差，则斜边为实长，高差所对内角为直线对基准面的倾角α，如图7-3所示。图7-4定比分割原理求直线的整数标高7.2.2.2直线的坡度和平距直线上任意两点的高差与其水平距离之比称为该直线的坡度。......
2023-06-22
-
地形面标高投影优化方案详细阅读
如图7-20所示，画出地面等高线的水平投影并标注其高程，即得地形面的标高投影，地形面的标高投影也称地形图。图7-21地形图地形面的标高投影，称为地形图，如图7-21所示。图中每隔4根画得较粗，并注有标高数字，单位为m的等高线，称为计曲线，不加粗的等高线称为首曲线。......
2023-06-22
-
各位置平面投影的特点详细阅读
特殊位置平面又分为投影面垂直面和投影面平行面两种，特殊位置平面的投影特性如下。例3-13如图3-37所示，已知平面的正面投影和侧面投影，求作水平投影。侧垂面的水平投影与正面投影有类似性。表3-5立体上的投影面平行面续表3.一般位置平面的投影特性相对三个投影面都倾斜的平面称为一般位置平面，如图3-38所示，由于它相对三个投影面都倾斜，所以它的三个投影都不反映实形，但具有类似性。......
2023-06-28
-
点、直线、平面的投影学习指南详细阅读
本章的地位及特点本章介绍正投影图的基本知识，包括点的投影规律、各种位置直线的投影特性及不同相对位置两直线的投影特性、各种位置平面投影特性，以及点、线、面之间的从属关系，直线与平面的平行和相交关系等。正投影是平行投影的特例，因此平行投影的基本性质是建立正投影的基础。第2章介绍了工程中表示物体的常用方法，本章从点的投影开始，逐步深入地讨论用于表达物体正投影的方法。......
2023-06-28
-
平面辅助投影：换面法详细阅读
图3-49将一般位置平面变为投影面垂直面例3-22求△ABC对H面的倾角α。图3-52将一般位置平面变为投影面平行面作图作图方法如图3-52所示，先换H面，得到投影面垂直面的投影及β角，然后换V面得到△ABC的实形。......
2023-06-28
-
点、直线、平面的投影简介详细阅读
2-19一等腰直角△ABC，AC为斜边，顶点B在直线NC上，完成其两面投影。2-20已知菱形ABCD的对角线BD的投影和另一对角线端点的水平面投影a，试完成菱形的投影图。2-25完成下列平面图形的第三投影，并求作出属于平面上的点K的另两个投影，并填空。2-26作图判断点A或直线AB是否属于给定的平面。2-34过已知点A作一直线AB，使其平行于已知平面△DEF。2-36求作直线与平面的交点K，并判断可见性。......
2023-06-15
相关推荐