2-19一等腰直角△ABC，AC为斜边，顶点B在直线NC上，完成其两面投影。2-20已知菱形ABCD的对角线BD的投影和另一对角线端点的水平面投影a，试完成菱形的投影图。2-25完成下列平面图形的第三投影，并求作出属于平面上的点K的另两个投影，并填空。2-26作图判断点A或直线AB是否属于给定的平面。2-34过已知点A作一直线AB，使其平行于已知平面△DEF。2-36求作直线与平面的交点K，并判断可见性。......
2025-09-29
直线的标高投影解析
【摘要】：图7-2直线的标高投影为了更好的了解这两种表示方法，我们先来关注以下两个问题。以直线的标高投影为一条直角边，另一条直角边为直线两端点的高差，则斜边为实长，高差所对内角为直线对基准面的倾角α，如图7-3所示。图7-4定比分割原理求直线的整数标高7.2.2.2直线的坡度和平距直线上任意两点的高差与其水平距离之比称为该直线的坡度。
在标高投影中，直线的位置是由直线上的两个点或直线上一点及该直线的方向确定。因此，直线的表示法有以下两种。
（1）直线的水平投影并加注直线上两点的高程，如图7-2 （a）所示。
（2）直线上一个点的标高投影并加注直线的坡度和方向表示，如图7-2 （b）所示。
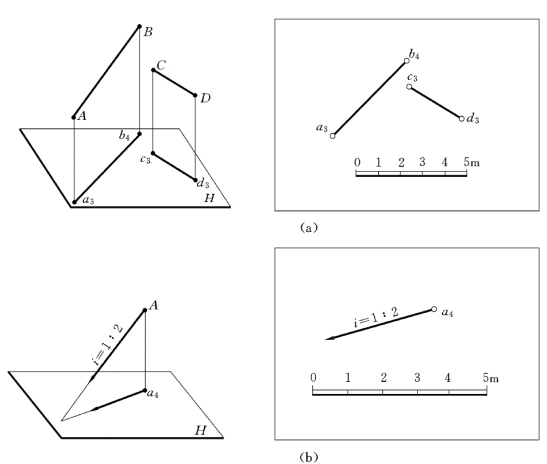
图7-2 直线的标高投影
为了更好的了解这两种表示方法，我们先来关注以下两个问题。
7.2.2.1 直线的实长及整数标高点
在标高投影中求直线的实长，仍然采用正投影中直角三角形法。以直线的标高投影为一条直角边，另一条直角边为直线两端点的高差，则斜边为实长，高差所对内角为直线对基准面的倾角α，如图7-3所示。
图7-3 直线的实长
在实际工作中，有时遇到直线两端点的标高并非整数，需要在直线的投影上标出各整数标高点的位置。解决这类问题，可利用定比分割原理作图，如图7-4所示。
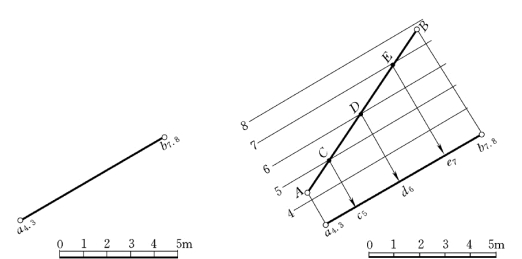
图7-4 定比分割原理求直线的整数标高
7.2.2.2 直线的坡度和平距
直线上任意两点的高差与其水平距离之比称为该直线的坡度。(https://www.chuimin.cn)
上式亦表明两点间水平距离为1个单位时两点间的高差即为坡度。
当两点间的高差为1个单位时它的水平距离称为平距。
由此可见，平距和坡度互为倒数。坡度越大，平距越小；反之，坡度越小，平距越大。
如图7-5所示，设直线上两点之间高差为ΔH，它们的水平距离为L。若用符号i和l分别表示坡度和平距，则有
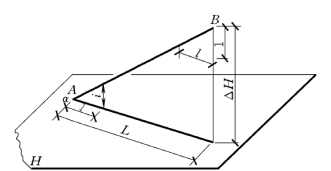
图7-5 直线的坡度和平距
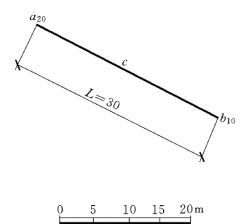
图7-6 求直线的坡度和C点标高
【例7-1】 求直线AB的坡度和平距，并求C点的标高，如图7-6所示。
解：为求直线AB的坡度与平距，先求出ΔH 和L，再利用定义式来确定直线的平距与坡度。
相关文章
- 详细阅读
-
点、直线、平面的正投影特点详细阅读
图2-9正投影的类似性2.2.1.4重合性两个或两个以上的点、线、面具有同一投影时，称为重合，这种投影性质称为正投影的重合性，如图2-10所示。......
2025-09-29
-
一般位置的直线投影及其特性介绍详细阅读
对一般位置直线来说，其实长和倾角不能直接在投影图中定出，可根据投影用作图的方法来求得，这种方法是直角三角形法。一般位置直线在三面投影体系中的直观图如图2-34所示。图中ab、a′b′是一般位置线AB 的两面投影，为已知条件。......
2025-09-29
-
正轴测投影的绘制方法详细阅读
此时在P面上所得到的投影称为正等轴测投影，简称正等测。这样便可按实际尺寸画图，但画出的图形比原轴测投影大些，各轴向长度均放大1/0.82≈1.22倍。图5-6斜垫块的正投影图5.2.1.2平面体的正等轴测投影的画法已知斜垫块的正投影图，画出其正等测图，如图5-6所示。如图5-13 所示，作楔形板上、下底面的轴测投影。......
2025-09-29
-
各位置平面投影的特性分析详细阅读
前两种属于特殊位置平面。两投影均为原图形的“类似形”。图2-49与投影面的垂直的平面的投影特性铅垂面；正垂面；侧垂面2.5.2.3一般位置平面一般位置平面指与H、V、W 均倾斜的平面，其投影特点是：V、H、W 投影均为原图形的“类似形”，任一投影均不能直接反映出平面与某投影面的夹角，也不能直接反映出平面的实形。......
2025-09-29
-
空调器的基本工况解析详细阅读
空调器的基本工况，主要包括制冷、制热和除湿三个方面，它们都是通过一定的人工技术来实现的。如此周而复始，便形成了空调器的制冷循环。在小型空调器中节流降压装置采用的是毛细管，而在大、中型空调器中节流降压装置则采用的是膨胀阀。在空调器中空气循环是分别利用室内外机中的电动风扇进行的。......
2025-09-29
-
平面内点与直线的关系详细阅读
图2-52平面上的直线的投影规律2.5.3.2平面内与投影面平行的直线凡在平面内平行于某一投影面的直线，称为投影面的平行线，可分为以下三种情况。平面上与投影面倾角最大的直线称为最大斜度线。......
2025-09-29
-
直观易懂的直线透视技巧详细阅读
3）连FN 得AB直线的全透视。图6-7视线法求H 面平行线的透视求透视；求次透视6.2.4.2H 面垂直线的透视作法H 面垂直线的透视仍为一垂直线。图6-8求作透视和次透视H 面垂直线的空间状况；H 面垂直线的求作解：透视求作。已知A 的次透视为a0，A 点离开H 面高度为h，求A0，如图6-9所示。......
2025-09-29
相关推荐