圆周的透视优化探讨

2023-06-22 理论教育版权反馈

【摘要】：图6-26圆周的透视性质解：因H 面投影K 位于o′x′之后，所以可以肯定K0是椭圆。同样在边线上作出8点，求得这8点的透视再连成圆周透视。

6.4.1.1　圆周的透视性质

（1）圆周平行于画面时，其透视仍为圆周，且圆周本身的圆心及半径的透视，为透视圆周的圆心和半径。

（2）圆周平面通过视点时，其透视为一直线。

（3）在其他位置时，根据圆周对画面和视点的相对位置不同，可为圆周、椭圆抛物线及双曲线（见图6-26）。

除了基面H、画面V 和视点S 外，过S点尚有一个平行于画面的平面N，称为消失面。因为通过N 上点的视线，将与画面V 平行，与V 面交于V 面上无限远处，即这种点的透视消失于画面上无限远处。消失面N 与基面H 相交于一条与基线OX 平行的直线n—n，称为消失线。

1）当圆周a与n—n不相交时，其透视a0是个椭圆（特殊情况下可以是圆）。

2）当圆周b与n—n相切时，其透视b0是抛物线。

3）当圆周c与n—n相交时，其透视c0是双曲线。

大部分情况下，空间的圆周都位于视点之前，故透视为椭圆。当然，透视为圆周或直线只是特殊情况。作圆周的透视，就是在圆周上取一些点，求出这些点的透视；再用光滑曲线连接起来即可。

6.4.1.2　8点法作圆周的透视椭圆

【例6-12】　作H 面上圆周K 的透视K0。

pagenumber_ebook=99,pagenumber_book=87

图6-26　圆周的透视性质

解：因H 面投影K 位于o′x′之后，所以可以肯定K0是椭圆。

（1）外切正方形线不平行画面时，如图6-27 （a）所示。

先作出K的外切正方形abeg，与圆周K切于四边中点1，3，5，7，再连对角线ae，bg，与K交于2，4，6，8四点，求出此8点的透视，即可连得K的透视K0。

作法如下：

1）用视线法或交线法求得正方形边线的透视。

pagenumber_ebook=99,pagenumber_book=87

4）将所得8点连成一个椭圆即为K0。

（2）外切正方形的二边线平行画面，如图6-27 （b）所示。

与画面平行的一组边线的透视，仍平行于o′x′，另一组垂直于画面的直线。它们的灭点为s′。同样在边线上作出8点，求得这8点的透视再连成圆周透视。具体的作法在此不再详细写出。

6.4.1.3　8点法作竖直面上圆周的透视

【例6-13】　用8点法作竖直面上圆周的透视，并设其下端切于H面，如图6-28所示。

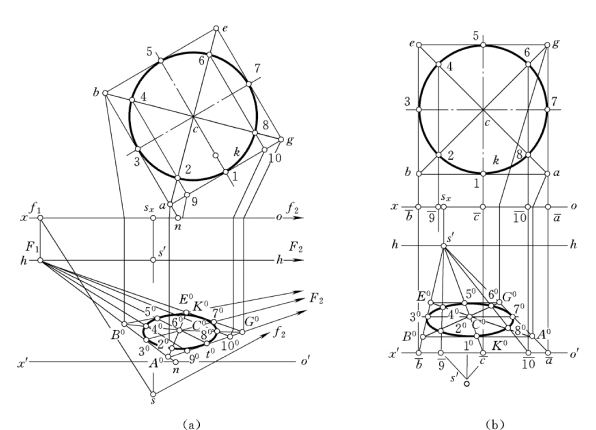
pagenumber_ebook=100,pagenumber_book=88

图6-27　作H 面上圆周的透视

（a）外切正方形线不平行画面；（b）外切正方形的二边线平行画面

解：用视线法作出外切正方形的透视，高度用真高线nN 作出。

（1）延长ab交ox 于n，在V 面上作出o′x′上的n，作真高线得Nn因圆下端与H 面相切，所以Nn=半径，在V 面作出半圆，圆心为¯C，并在半圆上作出2，4点，并由之作平行于ox的直线得2，4。

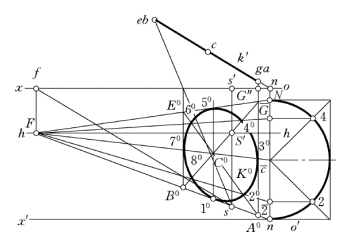
pagenumber_ebook=100,pagenumber_book=88

图6-28　8点法作竖直面上圆周的透视

pagenumber_ebook=100,pagenumber_book=88

（4）连接这8点得圆的透视K0。