作平面立体的透视实为作立体的棱线的透视。图6-13交线法作正方体的透视解：先作出其两个方面的灭点F1，F2。......
2023-06-22
实现平面立体的一点透视法
【摘要】：3）连s′n得ab的全透视。图6-22距点法求作基面上矩形的平行正透视1）以sx为圆心，ssx为半径作弧交ox轴于d，由之作连系线交h—h于D （距点）。
6.3.5.1 距点法求作基面上矩形的平行正透视
（1）求作基面上矩形的平行正透视的实质，就是求作矩形中与画面垂直的两条边的透视。
（2）基面上矩形与画面迹线的相对位置有三种情况：相切、相离、相交。
（3）作法如下，如图6-22所示。
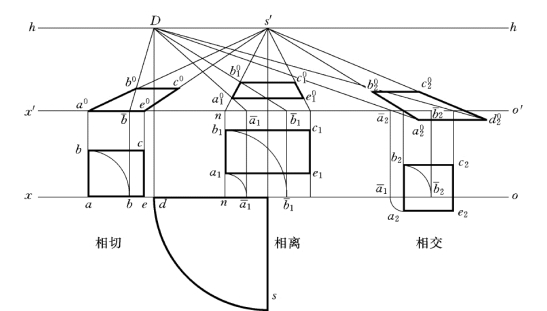
图6-22 距点法求作基面上矩形的平行正透视
1）以sx为圆心，ssx为半径作弧交ox轴于d，由之作连系线交h—h于D （距点）。
2）ab （延长ab）交ox于a （n），由之作连系线交o′x′于a （n）。
3）连s′n得ab的全透视。
5）过a0、b0做平行线交cd直线的全透视得
。
6.3.5.2 应用距点法求作长方体的平行正透视
【例6-11】 已知的长方体在H 面上正投影以及高为H，且已知视点在H 面上正投影s，如图6-23所示，求透视。
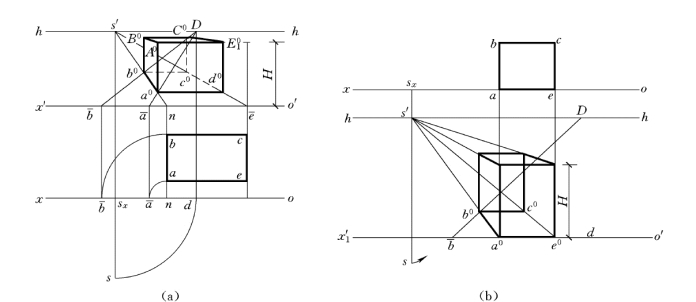
图6-23 应用距点法求作长方体的平行正透视
解：
（1）先用距点法求得长方体的次透视a0b0c0d0。
（2）在任一迹点上取真高等于H，连得长方体透视（灭点为主点s′）。
6.3.5.3 距点法求其他形体的一点透视
用距点法求其他形体的一点透视，其作法如图6-24、图6-25所示。
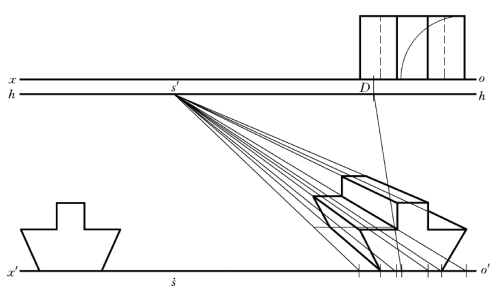
图6-24 距点法求斜面形体的一点透视
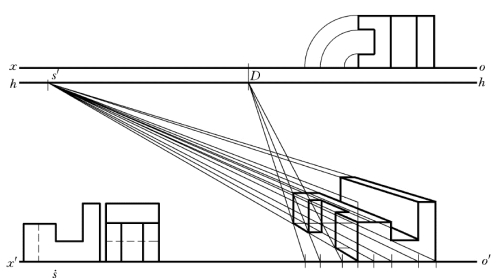
图6-25 距点法求复杂形体的一点透视
有关建筑工程制图的文章
- 详细阅读
-
如何制作平面透视？详细阅读
作平面图形的透视，实为作其边线的透视。这种利用两直线的透视的交点求作直线段透视的方法称为交线法。图6-11H 面垂直面的透视作法—视线法图6-11H 面垂直面的透视作法—视线法若连接Fn，则Fn为墙角线的透视。......
2023-06-22
-
平面立体截交线探究详细阅读
截切立体的平面称为截平面，截平面与立体表面的交线称为截交线，截交线所围成的平面图形称为截断面。求平面立体的截交线时，首先应确定平面立体的原始形状，进而分析其与投影面的相对位置；再分析截平面相对投影面和平面立体的位置，明确截交线的形状和投影特性，如积聚性、类似性等。分析截平面P与正四棱锥的四个侧棱面均相交，所以截交线为四边形。......
2023-06-28
-
平面与曲面的相交：立体几何优化详细阅读
平面立体与曲面立体的表面交线，一般是由数段平面曲线组合而成的空间曲线，如图4-18所示。因此，求作平面立体与曲面立体的相贯线，可归结为求作平面与曲面立体的截交线和求直线（棱线）与曲面立体表面的交点。其中除左边的棱面AB完全与半球相交外，其他两个棱面只部分与半球相交。因此，本题只需再作出相贯线的正面投影及侧面投影即可。......
2023-06-22
-
截面与平面立体相交的应用技巧详细阅读
图4-2求正垂面P与三棱锥的截交线解：从正面投影中可清楚地看到，截平面P与三棱锥的底面不相交，只与三个棱面相交。根据本题的特点，宜采用交点法作图。过1′、2′、3′向侧面引投影连接线，与s″a″、s″b″、s″c″相交，得1″、2″、3″。由于三棱锥各棱面的水平投影皆可见，故截交线的水平投影也都可见，画成实线；三棱锥侧面投影中SBC棱面不可见。......
2023-06-22
- 详细阅读
-
立体图形：两平面相交的几何模型详细阅读
两平面立体相交，其相贯线在一般情况下是封闭的空间折线，但有时也会是平面多边形。从图4-17中可以看出，相贯线（折线）上任一段直线都是甲平面立体的一个棱面与乙立体的一个棱面的交线。因此，求作两平面立体相贯线，实质上仍归结为求直线与平面的交点，以及求平面与平面交线的问题。求直立三棱柱与水平三棱柱的相贯线，如图4-17所示。......
2023-06-22
-
平面铣削加工：利用铣床实现大平面铣削加工详细阅读
铣削加工的主要内容如图3-78所示。镶齿端铣刀直径一般在φ75～φ300 mm，最大可达φ600 mm，主要用在立式或卧式铣床上铣削台阶面和平面，特别适合于大平面的铣削加工。端铣时，ap 为切削层深度；圆周铣削时，ap 为被加工表面的宽度。指平行于工作平面测量的切削层中最大的尺寸。......
2023-06-29
相关推荐