首页理论教育如何制作平面透视？

如何制作平面透视？

2025-09-29 理论教育版权反馈

【摘要】：作平面图形的透视，实为作其边线的透视。这种利用两直线的透视的交点求作直线段透视的方法称为交线法。图6-11H 面垂直面的透视作法—视线法图6-11H 面垂直面的透视作法—视线法若连接Fn，则Fn为墙角线的透视。

6.3.3.1　H 面平行面的透视作法

H 面平行面的灭线为视平线h—h。H 面平行面即水平面，为画面相交面的一种，故有灭线。过视点S作一平行于H 面的平面，它与画面相交成的灭线，即为视平线h—h。作平面图形的透视，实为作其边线的透视。所有边线的灭点，必在视平线h—h上。H 面上图形是H 面平行面的一种特殊情况，下面以H 面上图形的透视作法为例，介绍用交线法来求形体的两点透视，如图6-10所示。

【例6-3】　已知H面上有一矩形ABCD，其H面的正投影为abcd，视点S在H面的正投影为s，求矩形ABCD的透视与次透视。

解：

（1）先求连线的灭点，过s作sf1平行于ab交ox于f1，由之作连系线交h—h于F1。过s作sf2平行于ac交ox于f2，由之作连系交h—h于F2。因ab平行于cd所以F1也为cd的灭点，同样F2为bd的灭点。

（2）因a点在ox上，又因图形在H 面内，故A与a重合，亦在ox上，因A亦在V 面内，故A0与A重合。由a作连系交o′x′于A0 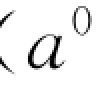（ pagenumber_ebook=89,pagenumber_book=77 ）。

（3）连A0F1、A0F2得直线AB、AC的全透视。

（4）延长bd和cd分别与ox交得它们的迹点1、2。由之作竖直线与o′x′交得迹点V面投影1′、2′，把它们分别与相应的灭点F1，F2相连，直线F21′、F12′就是直线BD、CD的全透视，这些直线与A0F1，A0F2相交得整个平面的透视。

pagenumber_ebook=89,pagenumber_book=77

图6-10　H 面上图形的透视作法——交线法

（5）次透视a0，b0，…因图形在H 面，所以与A0、B0、…重合。

这种利用两直线的透视的交点求作直线段透视的方法称为交线法。

6.3.3.2　H 面垂直面的透视作法

【例6-4】　设墙面上有一正方形窗框ABCD，其底边离开H 面高度等于正方形边长的一半。其H 面投影及视点位置如图，用视线法求其透视，如图6-11所示。

解：

（1）延长ab交ox于n，由之作投射线在V 面的o′x′轴上得迹点n。(https://www.chuimin.cn)

（2）过s作sf平行于ab交ox轴于f，由之作投射线交h—h于F （灭点）。

（3）连sa（d）、sb（c）交ox 于ax0（dx0），bx0（cx0）。

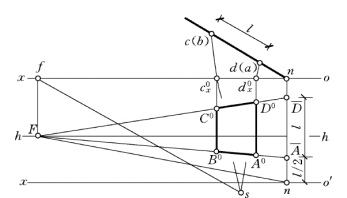
pagenumber_ebook=90,pagenumber_book=78

pagenumber_ebook=90,pagenumber_book=78

图6-11　H 面垂直面的透视作法—视线法

pagenumber_ebook=90,pagenumber_book=78

若连接Fn，则Fn为墙角线的透视。

6.3.3.3　V 面平行面的透视作法

【例6-5】　设正面墙上有一正方形窗框ABCD，其底边AB的高度等于正方形边长之半，其H 面投影及视点位置如图6-12所示，求透视。

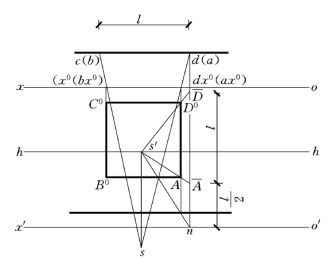
pagenumber_ebook=90,pagenumber_book=78

图6-12　V 面平行面的透视作法

解：

（1）因ABCD为V 面平行面，所以该平面上各线的灭点为主点s′，迹点为n。

pagenumber_ebook=90,pagenumber_book=78

（5）由A0、D0作水平直线交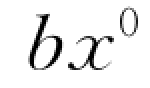 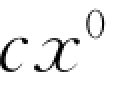pagenumber_ebook=90,pagenumber_book=78 （）的连系线于B0、C0，则A0B0C0D0就是所求作的透视。