圆锥的透视可先作出锥顶和底圆周的透视。已知横置于H 面上空心圆柱的H 面投影,如图6-29所示作透视。图6-30H 面上正圆柱的透视解:先按8点法作出底圆的透视。在过圆心的迹线上取真高作出圆锥的顶点E0。连接各点透视和两条外形素线得圆锥的透视。......
2023-06-22
6.2.4.1 H 面平行线的透视作法
H 面平行线是水平线。这里所讲的H 面平行线,仅指平行于H 面的画面相交线。
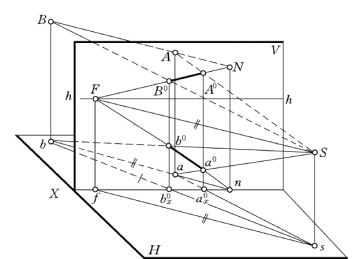
图6-6 H 面平行线的空间状况
(1)迹点作法和真高线。如图6-6所示,有一条H 面平行线AB,其在H 面上的投影为ab,ab//AB且等长,求作其透视A0B0,次透视a0b0。
延长AB与画面V 交得迹点N。此时ab亦必延长,与V 面交于ox 上的n点,n为ab的迹点。n为N 在H 面上的正投影,投射线Nn⊥ox。其高度Nn反映了AB 离开H 面的高度,故直线Nn称为H 面平行线的真高线(或量线)。
(2)灭点作法。H 面平行线的灭点位于视平线h—h 上。平行于直线AB 的视线SF,是一条H 面平行线,位于通过视点的水平视平面内。因h—h为该视平面与画面V的交线,故SF与V 面交成的灭点F 必位于h—h上。因ab//AB,故ab的灭点,与AB的灭点相同。即平行于ab的视线,也是一条H 面平行线,灭点F也在h—h上;且sf//ab,f在ox上,连系线Ff⊥ox。
(3)视线法作H 面平行线的透视和次透视,如图6-7所示,具体作法如下。
1)延长ab与ox交于n点;过n点作垂直线与o′x′交于V 面上n点,由之量取高度Nn=h就得迹点N。
2)过s作sf//ab交ox于f,过f作垂直线交h—h于F,则F为AB 直线和ab直线的灭点。
3)连FN 得AB直线的全透视。
4)连sa,sb交ox于ax0和bx0点,由ax0 和bx0 作连系线交FN 于A0,B0,则A0B0为直线AB的透视。
5)连Fn得ab直线的全透视。
6)过ax0,bx0作连系线交Fn于a0,b0,则a0b0 为直线ab的透视,AB的次透视。
这种利用直线的迹点,灭点和视线在H 面上投影求作直线段透视的方法,称为视线法。它是作建筑物的透视图时最常用的方法,故也称为建筑师法。
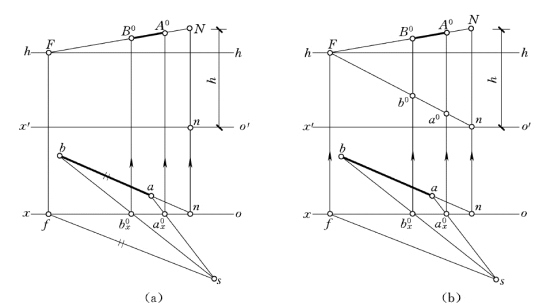
图6-7 视线法求H 面平行线的透视
(a)求透视;(b)求次透视
6.2.4.2 H 面垂直线的透视作法
H 面垂直线的透视仍为一垂直线。可利用通过它端点的水平辅助线来进行作图。H面垂直线实际上就是空间的竖直线,即铅垂线。
【例6-1】 已知H 面垂直线Aa,其在H 面上的正投影为a,其中Aa的高度等于h,求作直线Aa的透视和次透视,如图6-8所示。
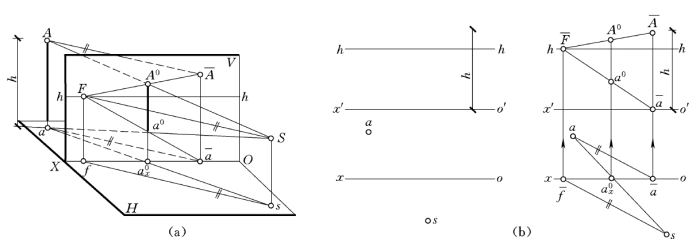
图6-8 求作透视和次透视
(a)H 面垂直线的空间状况;(b)H 面垂直线的求作
解:
(1)透视求作。

H 面垂直线为V 面平行线,其透视A0a0方向与直线Aa方向相同,仍为竖直方向。
(2)H 面垂直线在透视作图中应用——作空间点的透视。
如已知一点的次透视,并知该点离开H 面高度,则作点的透视可利用投射线。
【例6-2】 已知A 的次透视为a0,A 点离开H 面高度为h,求A0,如图6-9所示。
解:

![]()
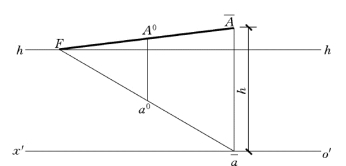
图6-9 H 面垂直线的应用
有关建筑工程制图的文章

圆锥的透视可先作出锥顶和底圆周的透视。已知横置于H 面上空心圆柱的H 面投影,如图6-29所示作透视。图6-30H 面上正圆柱的透视解:先按8点法作出底圆的透视。在过圆心的迹线上取真高作出圆锥的顶点E0。连接各点透视和两条外形素线得圆锥的透视。......
2023-06-22

若标准方向为磁子午线方向,则称磁方位角,用Am表示。测量中常把直线前进方向称为正方向,反之称为反方向。如图10-13所示,设A为AB直线的起端,B为终端,则Aab为正真方位角,Aba为反真方位角。......
2023-08-20

1)直线的透视特性直线的透视及基透视,一般情况下仍是直线。迹点的透视即为其本身,其基透视则在基线上。直线的透视必通过直线的画面迹点,直线的基透视必通过该迹点在基面上的正投影。直线上离画面无穷远点的透视,称为直线的灭点,直线的透视延长后一定通过灭点。把直线的迹点和灭点相连可得直线的全长透视。......
2023-09-24

确定一条直线的方向称为直线定向。进行直线定向,首先要选定一个标准方向线作为直线定向的依据,在测量中常以真子午线或磁子午线作为基本方向。磁子午线可用罗盘仪测定。两者之间的夹角称为磁偏角,用δ表示,如图10-10所示。地球磁极是不断变化的,北磁极正以每年10km的速度向地理北极移动。此外,罗盘仪还会受到地磁场及磁暴的影响。图10-10 真子午线和磁子午线地面上不同经度的子午线收敛于两极。......
2023-08-20

续表考点:圆的方程(2016卷II,4)圆x2+y2-2x-8y+13=0的圆心到直线ax+y-1=0的距离为1,则a=().A.-B.-C.D.21.已知圆C:(x-1)2+(y-2)2=2与y轴在第二象限所围区域的面积为S,直线y=2x+b分圆C的内部为两部分,其中一部分的面积也为S,则b=().A.-B.±C.-D.±2.(2016河南洛阳四模)距某码头400km......
2023-10-15

当画面与立体的主要立面平行时,所得的透视称为平行透视。由于画面同时平行于立体的长度和高度方向,这两个方向直线的透视没有灭点,而宽度方向直线垂直于画面,其透视灭点就是主点,所以平行透视只有一个灭点,故又称为一点透视。图8—21台阶的平行透视使台阶的前立面在画面上,确定站点s,并根据台阶立面图高度定出基线o′x′和视平线h—h的位置。例8—2作建筑物的室内透视图。......
2023-09-24

③近处的雪花较大,远处的雪花较小,符合透视原理。⑤用Photoshop自带的插件Camera Raw调整画面色调,其界面和操作与Lightroom完全相同。......
2023-06-23
相关推荐