图6-3圆柱正等轴测投影图的绘制（续）画出轮廓线；检查加深；圆柱正等轴测投影最后成图图D.3 流水线操作阶段如果我们假设每个流水线操作阶段有10ns的延迟，然后如果每条指令要求在下一条指令获得前执行完成，那么每条指令就花40ns。这种情况下，处理器一次执行4条指令。只有当流水线操作接到一个稳定的指令流，并不受限制地使用所需操作数作为指令的输入输出，才能达到这样的性能。......
2023-06-23
正轴测投影的绘制方法
【摘要】：此时在P面上所得到的投影称为正等轴测投影，简称正等测。这样便可按实际尺寸画图，但画出的图形比原轴测投影大些，各轴向长度均放大1/0.82≈1.22倍。图5-6斜垫块的正投影图5.2.1.2平面体的正等轴测投影的画法已知斜垫块的正投影图，画出其正等测图，如图5-6所示。如图5-13 所示，作楔形板上、下底面的轴测投影。
5.2.1.1 正等轴测投影
当投射方向S垂直于轴测投影面P时，形体上三个坐标轴的轴向变形系数相等，即三个坐标轴与P面倾角相等。此时在P面上所得到的投影称为正等轴测投影，简称正等测。
根据计算，正等测的轴向变形系数p=q=r=0.82，轴间角∠X1O1Z1=∠X1O1Y1=∠Y1O1Z1=120°。画图时，规定把O1Z1轴画成铅垂位置，因而O1X1轴与水平线均成30°角，可直接用30°三角板作图，如图5-3所示。
为作图方便，常采用简化变形系数，即取p=q=r=1。这样便可按实际尺寸画图，但画出的图形比原轴测投影大些，各轴向长度均放大1/0.82≈1.22倍。
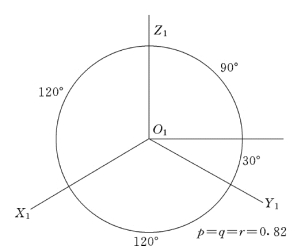
图5-3 正等测的轴间角和轴向变化率
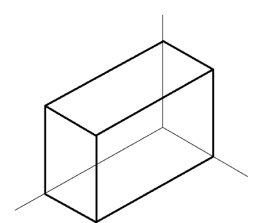
图5-4 轴向变化率为0.82的正等测图
图5-4是根据图5-1中的三面正投影图，按轴向变形系数为0.82画出的正等测图。图5-5是按简化轴向变形系数为1画出的正等测图。
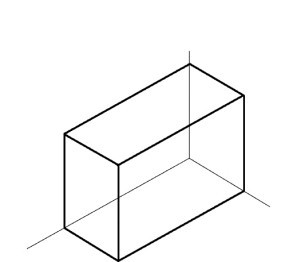
图5-5 轴向变化率为1的正等测图
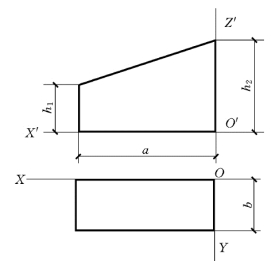
图5-6 斜垫块的正投影图
5.2.1.2 平面体的正等轴测投影的画法
【例5-1】 已知斜垫块的正投影图，画出其正等测图，如图5-6所示。
解：
（1）在斜垫块上选定直角坐标系。
（2）如图5-7（a）所示，画出正等轴测轴，按尺寸a、b，画出斜垫块底面的轴测投影。
（3）如图5-7 （b）所示，过底面的各顶点，沿O1Z1方向，向上作直线，并分别在其上截取高度h1和h2，得斜垫块顶面的各顶点。
（4）见图5-7 （c）所示，连接各顶点，画出斜垫块顶面。
（5）见图5-7 （d）所示，擦去多余作图线，描深，即完成斜垫块的正等测图。
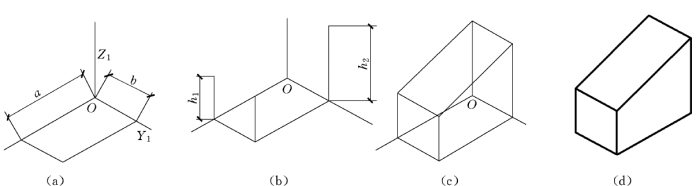
图5-7 斜垫块的正等测图
【例5-2】 已知基座的正投影图，画出其正等测图，如图5-8所示。
解：
（1）如图5-8所示，在基座上选定直角坐标系。
（2）如图5-9 （a）所示，画出正等轴测轴，根据正投影图，画出矩形底块上底面的正等测。
（3）如图5-9 （b）所示，沿O1Z1轴的方向，向下画出矩形块的厚度。
（4）如图5-9 （c）所示，根据尺寸a、b，定出锥台各侧棱线与矩形块上底面的交点的位置。
（5）如图5-9 （d）所示，根据尺寸c、d和h，画出锥台上底面的正等测。
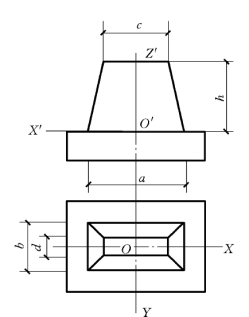
图5-8 基座的正投影图
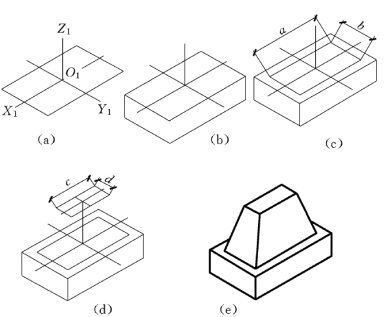
图5-9 基座的正等测图
（6）如图5-9 （e）所示，画出锥台各棱线。擦去多余作图线，描深，即完成基础墩的正等测图。
【例5-3】 已知台阶正投影图，画出其正等测图，如图5-10所示。
解：
（1）如图5-10所示，在台阶上选定直角坐标系。
图5-10 台阶的正投影图
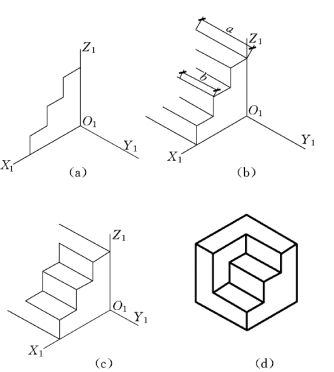
图5-11 台阶的正等测图
（2）如图5-11 （a）所示，画出轴测轴，根据正投影图画出台阶前端面的轴测投影。
（3）如图5-11 （b）所示，过前端面的各角点，沿O1Y1轴方向，由前向后作直线，并对应截取长度a和b。
（4）如图5-11 （c）所示，画出踏步的正等测。
（5）如图5-11 （d）所示，画出栏板的正等测。擦去多余作图线，描深，即完成台阶体的正等测图。
【例5-4】 已知形体的正投影图，画出其正等测图，如图5-12所示。
解：
（1）如图5-13 （a）所示，画出正等测轴，根据正投影图，画出矩形底块的轴测投影。
（2）如图5-13 （b）所示，作楔形板上、下底面的轴测投影。
1）自原点O1沿O1Z1轴向上量取20mm得点E1。
2）过点E1作O1X1轴平行线，并在其上自点E1向右量取6mm得点A1，再量取6mm，得点B1。
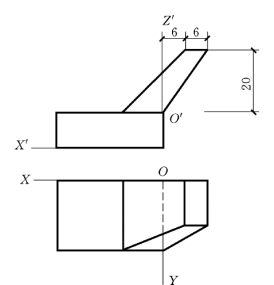
图5-12 形体的正投影图
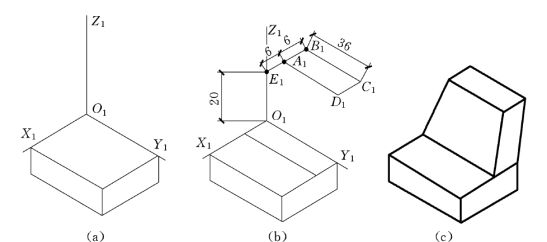
图5-13 形体的正等测图
3）分别过点A1和B1作O1Y1轴平行线，并在其上分别沿O1Y1方向量取楔形板上底面的长度尺寸，得点C1和D1。平面图形A1B1C1D1即为上底的轴测投影。
4）在O1X1Y1面上，作出楔形板下底面的轴测投影。
（3）如图5-13 （c）所示作出各侧棱线，擦去多余作图线，描深，即完成形体的正等测图。
5.2.1.3 圆的正等测投影和画法
一般情况下，圆的正等测投影为椭圆。画圆的正等测投影时，一般以圆的外切正方形的轴测投影——菱形，然后，再用四心法近似画出椭圆。
图5-14 圆的正投影图
现以图5-14所示水平圆为例，介绍圆的正等测投影和画法。
（1）在图5-14所示的正投影图上，选定坐标原点和坐标轴。并沿坐标轴方向作出图的外切正方形，得正方形与圆的四个切点A、B、C和D。
（2）如图5-15 （a）所示，画出正等轴测轴O1X1和O1Y1。沿轴截取O1A1=OA，O1B1=OB，O1C1=OC，O1D1=OD，得点A1、B1、C1和D1。
（3）如图5-15 （b）所示，过点A1、B1作直线平行于O1Y1轴，过点C1、D1作直线平行于O1X1轴，交得菱形A1B1C1D1，此即为圆的外切正方形的正等测投影。
（4）如图5-15 （c）所示，以点O0为圆心，以O0B1为半径作圆弧B1D1；点O2为圆心，以O2A1为半径作圆弧A1C1。
图5-15 圆的正等测图的近似画法
（5）如图5-15 （d）所示，线段O0B1、O0D1分别与菱形长对角线交于点O3、O4。以点O3为圆心，O3A1为半径作圆弧A1D1；以点O4为圆心，O4C1为半径作圆弧C1B1。以上四段圆弧组成的近似椭圆，即为所求圆的正等测投影。
图5-16是三个坐标面上相同直径圆的正等测投影，它们是形状相同的三个椭圆。
每个坐标上圆的轴测投影（椭圆）的长轴方向与垂直于该坐标面的轴测轴垂直；而短轴测与该轴测轴平行。
以上圆的正等测的近似画法，也适用于平行坐标面的圆角。
图5-17 （a）所示，平面图形上有四个圆角，每一段圆弧相当于整圆的1/4。其正等测如图5-17 （b）所示。每段圆弧的圆心是过外接菱形各边中点 （切点）所作垂线的交点。
图5-17 （c）是平面图形的正等测。其中圆弧D1B1是以O2为圆心，R2为半径画出；圆弧B1C1是以O3为圆心，R3为半径画出。D1、B1、C1等各切点，均利用已知的r来确定。
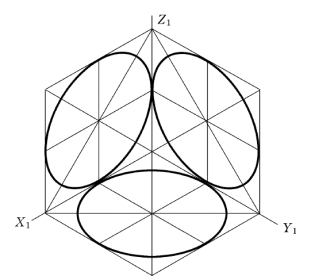
图5-16 各坐标面上圆的正等测投影图
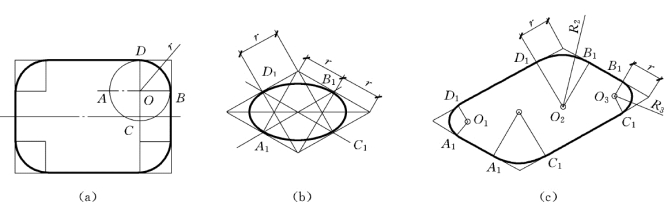
图5-17 圆角正等测画法
5.2.1.4 曲面立体正等测投影图的画法
【例5-5】 已知柱基的正投影图，画出其正等测图，如图5-18所示。
解：
（1）如图5-18 （a）所示，在柱基上选定直角坐标系。
（2）如图5-18 （b）所示，画出轴测轴，根据正投影图，画出方形底块上底面的正等测投影。
（3）如图5-18 （c）所示，沿O1Z1轴方向，向下量取尺寸h1，画出底块的厚度。
（4）如图5-18 （d）所示，画出坐标面XOY内的柱墩底圆和高度为h2的顶圆的正等测投影。
（5）如图5-18 （e）所示，作出两椭圆的公切线。擦去多余作图线，描深，即完成柱基的正等测图。
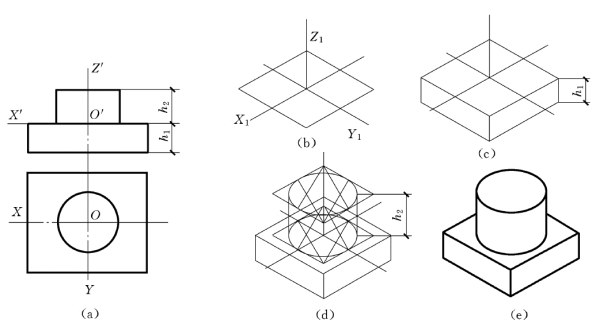
图5-18 柱基的正投影图与正等测图
【例5-6】 画出所示圆柱左端被切割后的正等测图，如图5-19所示。
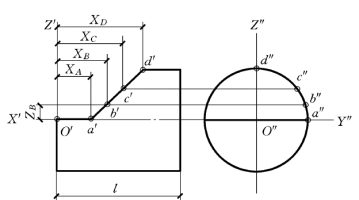
图5-19 带斜截面圆柱的正投影图
解：
（1）在圆柱体上选定直角坐标系。
（2）如图5-20 （a）所示，画出轴测轴，画出完整圆柱体两端面的投影。
（3）如图5-20 （b）所示，作两椭圆公切线，画出圆柱轴测投影。
（4）作截交线上若干点的轴测投影。
1）如图5-20 （b）所示，过O1Y1轴与椭圆的交点作直线平行于O1X1轴，并在该直线上量取长度XA，得点A1。
图5-20 带斜截面圆柱的正等测图
2）如图5-20 （c）所示，过O1Z1轴与椭圆的交点作直线平行于O1X1轴，并在该直线上量取长度XD，得点D1。
3）见图5-20 （d），自原点O1开始，沿O1Z1轴向上量取长度ZB，得点B0，再过点B0在Z1O1Y1面内作直线平行于O1Y1轴，过该直线与椭圆的交点作直线平行于O1X1轴，并在其上量取长度XB，得点B1。
4）见图5-20 （e），同法求得C1点。根据截交线的对称性，作出已知点A1、B1、C1、D1的对称点。
5）如图5-20 （f）所示，依次光滑连接各点。擦去多余作图线，描深，即完成带斜截面圆柱的正等轴测图。
有关建筑工程制图的文章
- 详细阅读
-
正棱柱的投影图绘制方法与分析详细阅读
当底面为正多边形时，称为正棱柱。棱柱的棱线相互平行且相等。例4-1根据直四棱柱的轴测图，画出其三投影图。图4-2直四棱柱的投影图分析图4-2所示为直四棱柱，将其放在三投影面体系中，使其上、下底面均为水平面，所有棱线均为铅垂线，所有棱面均垂直于水平面。图4-4正四棱柱表面上的点......
2023-06-28
-
三面投影图的绘制方法与应用详细阅读
这种关系常称为三面投影图的投影规律，简称三等规律。图2-16三面投影面2.2.2.3三面投影图的对应关系1.度量对应关系三面投影图是在物体安放位置不变的情况下，从三个不同方向投影所得到的，它们共同表达同一物体，因此它们之间存在着紧密的关系。......
2023-06-22
-
机械图样的绘制与识读-轴测图绘制方法详解详细阅读
项目四轴测图项目要求在产品说明书、产品用户指南等文件资料中，有时需要提供产品的轴测图。所以工程技术人员要掌握轴测图的基本概念和绘制方法。轴测轴上的线段与空间坐标轴上的对应线段的长度比，称为轴测图的轴向缩短系数。图4-2正等轴测图的轴间角和轴向缩短系数为简化作图，常采用简化轴向缩短系数。坐标法是画轴测图最基本的方法。图4-10半圆和1/4圆弧的正等轴测图画法析。......
2024-10-25
-
轴测投影的基本概念与特性详细阅读
图5-2轴测图的形成5.1.2.3轴测投影种类1.根据投影线和轴测投影相对位置分类将形体斜放。其中，正等轴测投影、正二等轴测投影和斜二等轴测投影在工程上常用，本章只介绍正等轴测投影和斜二等轴测投影。......
2023-06-22
-
轴测投影的基本概念与技巧详细阅读
用正投影法形成的轴测图称为正轴测图，用斜投影法形成的轴测图称为斜轴测图。图6-5轴测图的形成6.1.2轴测图的相关术语1.轴测投影面得到轴测投影的平面，称为轴测投影面，一般用字母P 表示。......
2023-06-23
-
避免垂直轴测投影面的轴测图制作技巧详细阅读
绘制轴测图时，应注意避免组成直角坐标系的三根轴中的任意一根垂直于所选定的轴测投影面。因为当投影方向与坐标轴平行时，轴测图将失去立体感，变成后续课程所描述的三视图中的一个视图，如图2-25所示。图2-24轴测图的形成图2-25投射方向与坐标轴平行组成直角坐标系的三根轴在轴测投影面上的投影称为轴测轴。图2-27所示为同一立体的三种轴测图。......
2023-06-28
- 详细阅读
相关推荐