平面与曲面的相交：立体几何优化

2025-09-29 理论教育版权反馈

【摘要】：平面立体与曲面立体的表面交线，一般是由数段平面曲线组合而成的空间曲线，如图4-18所示。因此，求作平面立体与曲面立体的相贯线，可归结为求作平面与曲面立体的截交线和求直线（棱线）与曲面立体表面的交点。其中除左边的棱面AB完全与半球相交外，其他两个棱面只部分与半球相交。因此，本题只需再作出相贯线的正面投影及侧面投影即可。

平面立体与曲面立体的表面交线，一般是由数段平面曲线组合而成的空间曲线，如图4-18所示。每一段平面曲线都是平面立体的棱面与曲面立体表面的交线，相邻两段平面曲线的连接点（也称结合点，如1、2、3、4）是平面立体的棱线与曲面立体表面交点。

因此，求作平面立体与曲面立体的相贯线，可归结为求作平面（平面立体的棱面或底面）与曲面立体的截交线和求直线（棱线）与曲面立体表面的交点。

【例4-6】　求作四棱柱与圆锥的相贯线，如图4-18所示。

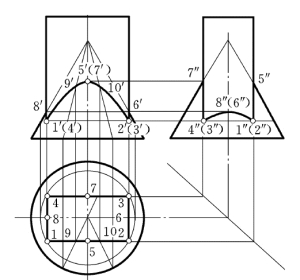
pagenumber_ebook=68,pagenumber_book=56

图4-18　四棱柱与圆锥相交

解：由于四棱柱的四个棱面皆为平行于圆锥轴线的铅垂面，因此，四棱柱和圆锥的相贯线是由四段双曲线组合而成（前、后两段及左、右两段各自对称）。四段双曲线的结合点恰是四棱柱的四条棱线与圆锥面的交点。

由于四棱柱各棱面的水平投影有积聚性，所以相贯线的水平投影全部与各棱面的水平投影重合（矩形），余下只需求作相贯线的正面投影及侧面投影即可。

作图步骤：

（1）求特殊点。

1）相贯线上的四个结合点（各段双曲线上的最低点）。这四个点的水平投影1、2、3、4为已知（在四根棱线的水平投影处），用纬圆法（圆锥面上过该四点的水平圆）求出它们的正面投影1′、2′、（3′）、（4′），再补出其侧面投影。

2）各段双曲线上的最高点。前、后两段双曲线上的最高点正好位于二立体左、右两部分的对称平面内，它们是圆锥面上最前、最后两根素线与四棱柱前、后两棱面的交点，可直接在侧面投影中定出，即5″、7″，交找到其正面投影5′、（7′）。同理，左、右两段双曲线上的最高点是圆锥面上最左、最右两根素线与四棱柱左、右两棱面的交点，可直接在正面投影中找到它们的6′、8′，然后再求出其侧面投影（6″）、8″。

（2）求一般位置的点。可用素线法（或纬圆法）求出前、后两段双曲线上两个处于对称位置的一般点，先在水平投影中取9、10两点，通过9、10分别作出圆锥面上的两条素线，并在两条素线的正面投影上定出9′、10′。

（3）连点。正面投影中的双曲线1′5′2′，与（4′）（7′）（3′）前后重影，左、右两段双曲线积聚成直线。侧面投影中的双曲线1″8″4″与（2″）（6″）（3″）左右重影，前、后两段双曲线积聚成直线。

【例4-7】　求三棱柱与半球的相贯线，如图4-19所示。

解：从水平投影中可看出，三棱柱的三个棱面都与半球相交。其中除左边的棱面AB完全与半球相交外，其他两个棱面只部分与半球相交。所以，相贯线应是由三段圆弧连接而成。由于三棱柱上的棱C与球并不相交，因此，相贯线的三段圆弧有两个结合点，它们分别在棱A和棱B 上。(https://www.chuimin.cn)

由于三棱柱各棱面的水平投影有积聚性，所以相贯线的水平投影全部积聚在三棱柱各棱面的水平投影上。因此，本题只需再作出相贯线的正面投影及侧面投影即可。从图中还可分析出：三棱柱后棱面（正平面）上的交线，其正面投影反映实形——圆弧，其侧面投影则积聚在后棱面的侧面迹线上；而其他两个棱面上的交线，在正面及侧面投影中皆为部分椭圆。

作图步骤：

（1）求棱面AC与半球的相贯线。棱面AC与半球底圆相交于1点，在正面投影中以0′为圆心0′1′为半径画圆，该圆与棱线a′的交点3为该截交线的终点（即与AB 棱面上另一段交线的结合点）。

（2）求棱面AB及BC与半球的相贯线。为求出这两个棱面上的交线，应先求出该两段交线上的特殊点。

1）结合点（即棱线B上的交点）。棱线B恰与半球的侧面投影轮廓线在同一平面内，且相交，故交点的位置可直接在侧面投影中定出，即6″，然后再找到6′。

2）棱面BC与半球的底圆相交，其交点的水平投影可直接定出，即9，然后找到9′及9″。

3）半球正面投影轮廓上的交点：AB与BC二棱面与半球的正面投影轮廓所在的平面皆为铅垂面，且相交，故交点的水平投影可直接定出，即4和8，然后再找出它们的另两个投影4′、4″和8′、（8″）。

pagenumber_ebook=69,pagenumber_book=57