立体图形：两平面相交的几何模型

2023-06-22 理论教育版权反馈

【摘要】：两平面立体相交，其相贯线在一般情况下是封闭的空间折线，但有时也会是平面多边形。从图4-17中可以看出，相贯线（折线）上任一段直线都是甲平面立体的一个棱面与乙立体的一个棱面的交线。因此，求作两平面立体相贯线，实质上仍归结为求直线与平面的交点，以及求平面与平面交线的问题。求直立三棱柱与水平三棱柱的相贯线，如图4-17所示。

两平面立体相交，其相贯线在一般情况下是封闭的空间折线，但有时也会是平面多边形。从图4-17中可以看出，相贯线（折线）上任一段直线都是甲平面立体的一个棱面与乙立体的一个棱面的交线。因此，求作两平面立体相贯线，实质上仍归结为求直线与平面的交点，以及求平面与平面交线的问题。

在运用表面取点法作题时，所求出的各点其连接原则如下。

（1）只有当被连接的两点既位于甲立体同一棱面，又位于乙立体同一棱面上时，方可进行连接。

（2）因为相贯线在一般情况下具有封闭性，故此每个点只应和相邻的两折点相连。

另外，连点时还要判别各段折线的可见性，其判别方法为：①只有位于两立体皆可见的棱面上的交线，才是可见的，画成实线；②两个相交的棱面中，只在其中有一个棱面为不可见，则它们的交线即为不可见，应画成虚线。

【例4-5】　求直立三棱柱与水平三棱柱的相贯线，如图4-17所示。

解：从水平投影可以看到，直立三棱柱部分地贯入水平三棱柱中；在侧面投影中可见水平三棱柱也部分地穿过直立三棱柱。因此，这两个三棱柱是相互贯穿（称为互贯），其相贯线为一组封闭的空间折线。

因为直立三棱柱的水平投影和水平三棱柱的侧面投影都有积聚性，所以相贯线的水平投影必然积聚在直立三棱柱的水平投影上；而相贯线的侧面投影一定积聚在水平三棱柱的侧面投影上。因此，只余下相贯线的正面投影需要进行作图。

通过对水平投影及侧面投影分析可知：只有直立三棱柱上的棱E和水平三棱柱上的棱A 和棱C参与了相交，且每条棱线上都各有两个交点，总共有6个交点（即所求的相贯线有6个折点）。

作图步骤：

（1）利用直立三棱柱各棱面的水平投影有积聚性，求出水平三棱柱上棱A与棱C 与直立三棱柱的DE 与EF 棱面的交点1、2、3、4 （直线与特殊位置平面相交，求交点）。

（2）利用水平三棱柱棱面投影有积聚性，求出直立三棱柱上棱E 与水平三棱柱的AB、BC侧面的交点5、6。

（3）确定连点顺序。相贯线上所有的6个交点全部求出后，应按照连点的原则将它们依次进行连接。

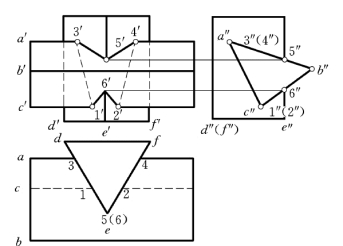
pagenumber_ebook=67,pagenumber_book=55

图4-17　直立三棱柱与水平三棱柱相交

从图4-17中可看出，3、5两点既在AB棱面上，又在DE棱面上，符合连点原则，因此可把3′5′连接起来。同理，1′3′、1′6′、6′2′、2′4′、4′5′等各点也都可以连接。这样就把所求出各点连成一条封闭的空间折线。

除了上述各点可以相互连接外，是否尚有其他可以连接的点呢？例如：1′、5′两点是否可以相连呢？ 1、5两点虽然都是DE棱面上的点，但1点和5点却又分别属于另外两个不同的棱面BC和AB，因此，这两点不能相连。

（4）判别可见性。在正面投影中，水平三棱柱上的AB棱面是不可见的，因此，位于此棱面上的折线段1、3和2、4的正面投影1′3′和2′4′为不可见，画成虚线。而其他棱面，如棱面AB和BC，以及直立三棱柱的棱面DE和EF，它们的正面投影皆为可见，所以处于这些棱面上的折线段的正面投影1′6′、6′2′、3′5′、5′4′等，皆为可见，一律画成实线。

（5）将相交二立体作为一个整体，补画全其轮廓线。棱线A和B 在交点3、4和1、2之间不应有线（3′4′和1′2′之间不应有线）；棱线D、F的正面投影d′与f′，各有一段被其前面的棱柱遮住，应画成虚线。

立体图形：两平面相交的几何模型

相关推荐