首页理论教育截平面与圆锥的交集

截平面与圆锥的交集

2023-06-22 理论教育版权反馈

【摘要】：平面截切圆锥时，根据截平面与圆锥线相对位置不同，圆锥面上产生五种不同形状的截交线。椭圆的长轴位于截平面内过椭圆中心的正平线上，其两端为Ⅰ及Ⅱ点。图4-8圆锥面上各种位置交线形状及投影图求作正垂面P与正圆锥的截交线，如图4-9所示。椭圆的正面投影与PV重影，其水平投影及侧面投影是椭圆。按1—3—5—7—2—8—6—4—1的顺序将所求各点的水平投影及侧面投影圆滑连接成椭圆。

平面截切圆锥时，根据截平面与圆锥线相对位置不同，圆锥面上产生五种不同形状的截交线。圆锥面上各种位置交线的形状及投影图，如图4-8所示。

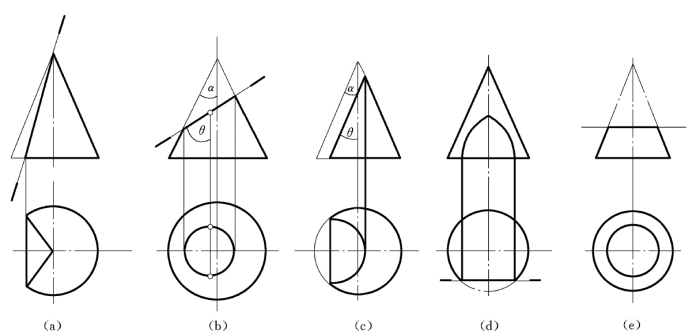
pagenumber_ebook=63,pagenumber_book=51

图4-8　圆锥面上各种位置交线形状及投影图

【例4-3】　求作正垂面P与正圆锥的截交线，如图4-9所示。

解：截平面P是正垂面，且θ＞α，所以它与圆锥面的交线是椭圆。椭圆的正面投影与PV重影（圆锥正面投影轮廓之间的一段直线），其水平投影及侧面投影是椭圆（但不反映实形）。

作图步骤：

（1）求特殊位置点。利用截平面正面投影有积聚性，可直接求出。

1）截交线的最高、最低点1、2；先在正面投影中定出1′、2′，再求水平及侧面投影，如图4-10所示。

2）截交线侧面投影的可见性分界点3、4；先定出3′、（4′）再利用投影关系直接求出3″、4″，最后求3、4。

3）椭圆长、短轴的端点。椭圆的长轴位于截平面内过椭圆中心的正平线上，其两端为Ⅰ及Ⅱ点。根据长、短轴相互垂直并且平分的几何关系，可知短轴必是一正垂线，其正面投影5′、（6′）积聚为一点，位于长轴正面投影的中点处。过5′、（6′）作纬圆，即可求出5、6和5″、6″，如图4 10所示。

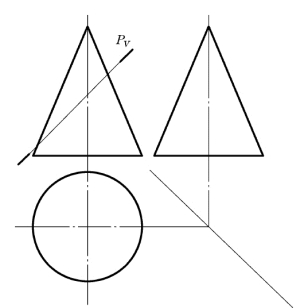
pagenumber_ebook=63,pagenumber_book=51

图4-9　正垂面与圆锥相交

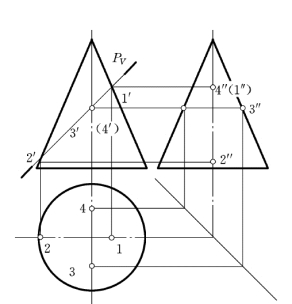
pagenumber_ebook=64,pagenumber_book=52

图4-10　求特殊位置点

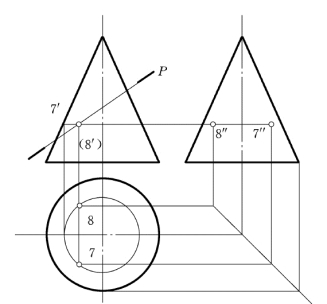
pagenumber_ebook=64,pagenumber_book=52

图4-11　求一般位置点

（2）求一般位置点。在已求出的特殊点之间空隙较大的位置上再定7′、（8′）两点通过作纬圆的办法找出7、8和7″、8″，如图4-11所示。

（3）连点并判别可见性。按1—3—5—7—2—8—6—4—1的顺序将所求各点的水平投影及侧面投影圆滑连接成椭圆（注意对称性）。由于3—1—4段位于右半侧圆锥面上，故其侧面投影为不可见，应将3″1″4″一段画成虚线，如图4-12所示。