直线的相对位置与交点分析介绍

2025-09-29 理论教育版权反馈

【摘要】：两直线的相对位置有以下三种：平行、相交、交叉。图2-43求相交两直线的投影已知图；作图解：根据相交直线的投影特点，可定出交点的V投影，利用交点可求出直线CD的V 投影。

两直线的相对位置有以下三种：平行、相交、交叉。交叉两直线称为异面直线，若两直线共面（位于同一平面内），则两直线必定平行或相交。

2.4.5.1　平行

1.投影特点

两直线在空间平行，则其各同面投影平行，如图2-39所示。

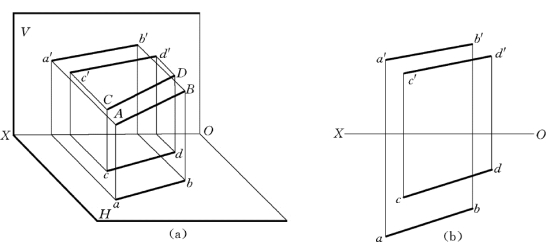
pagenumber_ebook=42,pagenumber_book=30

图2-39　两直线平行

（a）直观图；（b）投影图

2.两直线平行的判定

（1）若两直线的三组同面投影都平行，则两直线在空间平行。

（2）若两直线为一般位置直线，则只要有两组同面投影相互平行，即可判定两直线在空间平行。

（3）若两直线为某一投影面的平行线，则要用两直线在该投影面上的投影来判定其是否平行。

2.4.5.2　相交

1.投影特点

两直线在空间相交，则其各同面投影必相交，且交点符合点的投影规律，如图2-40所示。

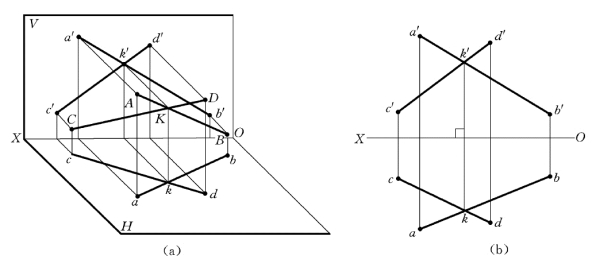
pagenumber_ebook=42,pagenumber_book=30

图2-40　两直线相交

（a）直观图；（b）投影图

2.两直线相交的判定

（1）若两直线的各同面投影都相交，且交点符合点的投影规律，则两直线为相交直线。

（2）对一般位置的两条直线而言，只要两组同面投影符合上述条件，就可判定两直线在空间是相交的。

（3）对两直线中有某一投影面的平行线时，则应验证直线在该投影面上的投影是否满足相交的条件，才能判定；也可以用定比性判定交点是否符合点的投影规律来验证两直线是否相交。

2.4.5.3　交叉(https://www.chuimin.cn)

1.投影特点

两直线在空间既不平行也不相交称为交叉。其投影特点是：同面投影可能有平行的，但不会全都平行；其同面投影可能有相交的，但其交点不符合点的投影规律，如图2-41所示。

2.交叉直线重影点可见性的判别

两直线交叉，其同面投影的交点为该投影面重影点的投影，可根据其他投影判别其可见性。

如图2-41所示，1、2点为H 面的重影点，通过V 投影可知1点在上，为可见点，2点在下，为不可见点；3、4两点为V 面的重影点，通过H 投影，可知3点在前，为可见点，4点在后，为不可见点。

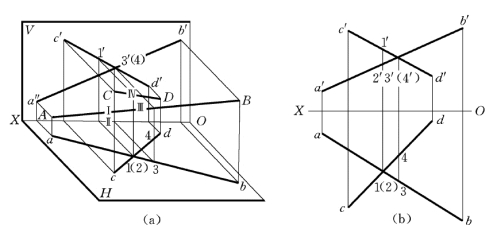
pagenumber_ebook=43,pagenumber_book=31

图2-41　两直线交叉

（a）直观图；（b）投影图

【例2-10】　已知等腰三角形ABC的一腰为AB，等腰三角形的底边BC在正平线BD 上，求此等腰三角形的投影，如图2-42 （a）所示。

解：根据等腰三角形的高垂直平分底边，并且已知底边在正平线BD上，根据直角定理，可在正面图上直接作出等腰三角形的高。即由A点作BD 线上的垂线AK，再在BD线上求出C点即可求出等腰三角形ABC。

作图步骤，如图2-42 （b）所示。

（1）在正面图上过a′点作a′k′⊥b′d′，并求出ak，则a′k′、ak，即为三角形高AK的投影。

（2）由于底边BD为正平线，所以正面投影反映实长。可量取b′k′=k′c′。并求出水平投影c点，即为等腰三角形的另一个顶点。

（3）连接a′c′和ac，即得所求等腰三角形的水平投影和正面投影。

pagenumber_ebook=44,pagenumber_book=32

图2-42　求等腰三角形的投影

【例2-11】　已知直线AB与CD 相交，求直线CD的V 投影，如图2-43所示。

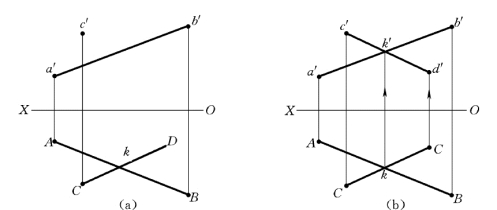
pagenumber_ebook=44,pagenumber_book=32

图2-43　求相交两直线的投影

（a）已知图；（b）作图

解：根据相交直线的投影特点，可定出交点的V投影，利用交点可求出直线CD的V 投影。

作图：过k向上引铅垂线与a′b′相交于k′，连接c′k′并延长，过d向上引铅垂线与c′k′的延长线交于d′，c′d′即为所求，如图2-43 （b）所示。