一般位置的直线投影及其特性介绍

2023-06-22 理论教育版权反馈

【摘要】：对一般位置直线来说，其实长和倾角不能直接在投影图中定出，可根据投影用作图的方法来求得，这种方法是直角三角形法。一般位置直线在三面投影体系中的直观图如图2-34所示。图中ab、a′b′是一般位置线AB 的两面投影，为已知条件。

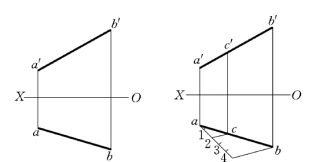
pagenumber_ebook=39,pagenumber_book=27

图2-33　直线上点投影的定比性

一般位置直线的投影有以下投影特性：三个投影都倾斜于投影轴，长度变短，不能反映直线与投影面的倾角。对一般位置直线来说，其实长和倾角不能直接在投影图中定出，可根据投影用作图的方法来求得，这种方法是直角三角形法。

一般位置直线在三面投影体系中的直观图如图2-34所示。

2.4.4.1　求直线段对H 面的倾角α及实长

pagenumber_ebook=40,pagenumber_book=28

图2-34　一般位置直线在三面投影体系中的直观图

如图2-35 （a）所示，在直角三角形AA1B中，斜边AB为线段实长，直角边BA1为水平投影ab之长，另一条直角边AA1则为AB两点的Z 坐标差，斜边AB与直角边BA1夹角为倾角α。

用直角三角形法求直线段AB的实长和对H面的倾角α，其作图方法，如图2-35 （b）所示。图中ab、a′b′是一般位置线AB 的两面投影，为已知条件。

过ab的端点a引ab的垂线，在该垂线上量取aA0=a′b′1（a′b′1为A、B 两点的Z 坐标之差）。连接bA0得一直角三角形abA0。在此直角三角形中，斜边bA0之长即为直线段AB之实长，α为所求倾角。

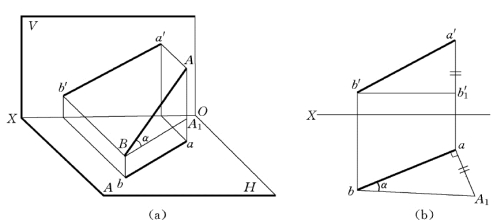
pagenumber_ebook=40,pagenumber_book=28

图2-35　求一般位置直线的实长与相对于H 面倾角α

2.4.4.2　求直线段对V 面的倾角β及实长

如图2-36 （a）所示，在直角三角形ABB1中，斜边AB为线段的实长，直角边AB1为a′b′之长，直角边BB1为B、A两点的y坐标差，斜边与直角边AB1的夹角为倾角β。

用直角三角形法求AB实长及倾角的方法，如图2-36 （b）所示，图中ab、a′b′为已知条件。

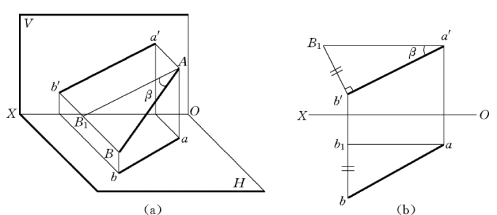
pagenumber_ebook=40,pagenumber_book=28

图2-36　求一般位置直线的实长与相对于V 面倾角β

过b′引a′b′的垂线，在该垂线上量取b′B0=ba1（ba1为B、A两点的y坐标之差），连接a′B0，得一直角三角形a′b′B0，在该直角三角形中斜边a′B0之长为直线段AB之实长，β为所求倾角。

求直线段实长及直线对W 投影面的倾角γ角的作图方法与上述方法类似，请读者自行分析。

由此可以归纳出：用直角三角形求一般位置直线市场与倾角的方法是，以直线的某一投影为直角边，直线的两个端点与这个投影面的距离差为另一直角边，所作出直角三角形的斜边即为实长，斜边与直线投影的夹角即为直线与这个投影面的真实倾角。

【例2-8】　已知直线AB的H 面的投影ab于在V 面的投影a′b′、求AB的实长及与V 面的倾角β。

解：已知a′b′和ab，需先求出A、B两点的z坐标之差，然后利用直角三角形定理作出直角三角形，求出倾角β的值，图2-37即为所求。

【例2-9】　已知直线AB和直线外一点C 的两面投影，求C点到直线AB 的距离，如图2-38 （a）所示。

解：过点作直线的垂线，垂线的实长即为点到直线的距离，因为AB为水平线，根据直角投影定理，在水平投影中过C点作直线AB 的垂线，其水平投影反映直角。

作图步骤，如图2-38 （b）所示。

pagenumber_ebook=41,pagenumber_book=29

图2-37　求直线的投影和倾角

（1）在水平面图上通过c点作ab的垂线得到交点k，k点即为垂足K 的水平投影。

（2）根据点的投影特性求出k′点。

（3）c′k′、ck分别为垂线CK 的正面投影和水平投影。

（4）在水平投影图上根据直角三角形法求出直线的实长，即为C点到直线AB 的距离（也可以在正面图上求垂线的实长）。

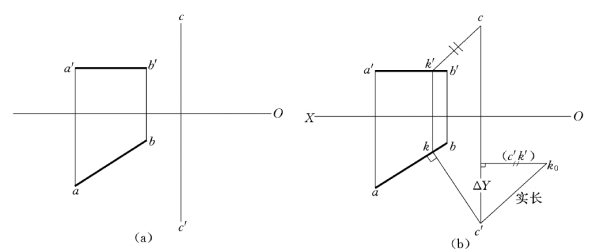
pagenumber_ebook=41,pagenumber_book=29

图2-38　求点到直线的距离