三面投影图的展开。图2-15形体三个视图2.3.2三面投影图的投影规律1.三面投影图的基本规律正面图与平面图长对正；正面图与侧面图高平齐；平面图与侧面图宽相等。这种关系称为三面投影图的投影规律，也称为三等关系。......
2023-06-23
点的投影规律及三面投影
【摘要】：点的投影与坐标的关系。图2-20点的三面投影图图2-21三个投影面体系及八个分角的划分两个互相垂直的投影面将空间分为四个象限；三个互相垂直的投影面将空间分为八个分角，如图2-21所示。若两点在某一投影面内的投影重合，则称它们为相对于该投影面的重影点，其可见性根据它们在另外两个投影面内的投影来判断。
（1）设立V、H、W 三个互相垂直的投影面。
（2）由空间一点A分别向投影面V、H、W 作垂线，垂足分别标记为a′、a、a″，称为点A的正面投影、水平投影和侧面投影，或简称为V 投影、H 投影和W 投影，如图2-20所示。
（3）点的投影与坐标的关系。将V、H、W看作三个坐标面，点A到W、V、H 三个坐标面的距离Aa″、Aa′和Aa分别称为点A 的x、y、z坐标。
Aa′、Aa″和Aa是三条互相垂直的直线，它们两两相交确定了三个互相垂直的平面，这三个平面与V、H、W 一起围成了一个“长方体”。平面Aa′a与X 轴的交点记为ax，平面Aa″a与Y轴的交点极为ay，平面Aa′a″与Z轴的交点记为az。
根据长方体各表面及棱线之间的关系 （平行、垂直）可知
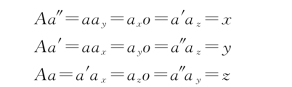
由上述关系看出，点的每个投影反映点的两个坐标。
（4）V、H、W 三投影面的展平，V 面不动，H 面绕X 轴向下转90°与V 面重合，W面绕Z轴向右转90°与V 面重合。
（5）展平后三面投影的位置关系。
1）V 投影与H 投影的连线a′a⊥OX。
2）V 投影W 投影的连线a′a″⊥OZ。
3）H 投影与W 投影有相同的Y坐标。
（6）上述关系可以看出，点在互相垂直的两投影面内的投影，当两投影面绕其交线展平到同一个平面内时，两投影的连线与轴（交线）垂直。
图2-20 点的三面投影图
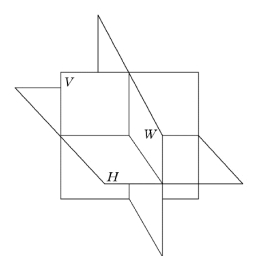
图2-21 三个投影面体系及八个分角的划分
（7）两个互相垂直的投影面将空间分为四个象限；三个互相垂直的投影面将空间分为八个分角，如图2-21所示。
（8）特殊位置点的投影。
1）点在某投影面内，该面的投影就是其本身。
2）点在某投影轴上，该点为两个平面所共有，在这两个投影面上的投影都是其本身。
（9）重影点。若两点在某一投影面内的投影重合，则称它们为相对于该投影面的重影点，其可见性根据它们在另外两个投影面内的投影来判断。可将不可见点的投影标记加小括号表示。
（10）两点的相对位置：①X 坐标大者为左，小者为右；②Y坐标大者为前，小者为后；③Z坐标大者为上，小者为下。
【例2-1】 已知四点A、B、C、D分别位于投影面和投影轴上 [见图2-22 （a）]，求作各点的三面投影图。
解：由图2-22（a）可知A点位于H面上，其水平投影a与A点重合，其正面投影a′和侧面投影a″分别位于OX轴和OY轴上；B点位于V面上，其正面投影b′与B点重合，水平投影b和侧面投影b″分别位于OX轴和OZ轴上；C点是W 面上的点，其侧面投影c″与C点重合，其正面投影c′和水平投影c分别位于OZ轴和OY轴上；D点位于OX轴上，其正面投影d′和水平投影d与D点重合位于OX轴上，侧面投影d″位于原点O上。
作图结果如图2-22 （b）所示，注意C点的水平投影c应在OYH轴上，A点的侧面投影a″应在OYW轴上。
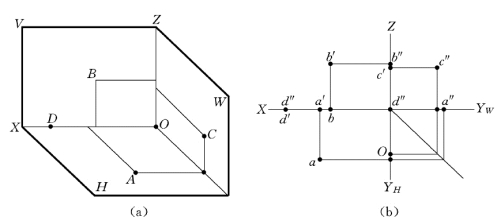
图2-22 特殊位置点的投影
（a）已知点；（b）作图结果
【例2-2】 如图2-23 （a）所示，已知点的两面投影求其第三投影。
解：根据点的已知两面投影可由点的投影规律求出其第三投影。
过a′向OZ轴引水平线并延长，过a引水平线与45°分角线相交并转折向上引铅垂线，该铅垂线与过a′所画水平线相交，交点即为a″；过b′向下画铅垂线，过b″向下画铅垂线与45°分角线相交再向左引水平线，该水平线与过b′所画铅垂线相交，交点即为b。
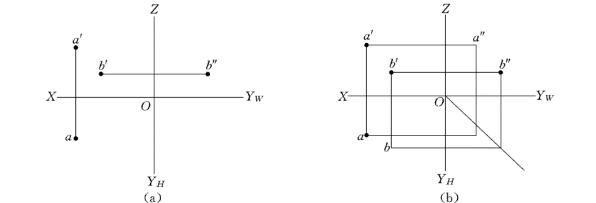
图2-23 点的第三面的投影
（a）已知点；（b）作图结果
【例2-3】 如图2-24 （a）所示，已知A、B两点的三面投影，判别两点的相对位置，并画出A、B两点的直观图。
解：由图2-24 （a）可知，A点的X 坐标大于B 点的X 坐标，A点的Y坐标大于B点的Y坐标，B点的Z坐标大于A 点的Z坐标，所以A点在B 点的左前下方。
直观图画法：首先画出一个三投影面体系 （注意：OY轴应画成45°斜线），然后在各个投影面上定出A、B两点的三面投影，过点的投影引该投影面的垂线，对应三条垂线的交点即为点的空间位置，如图2-24 （b）中的A、B两点即为所求。通过直观图可以验证A、B两点的相对位置。
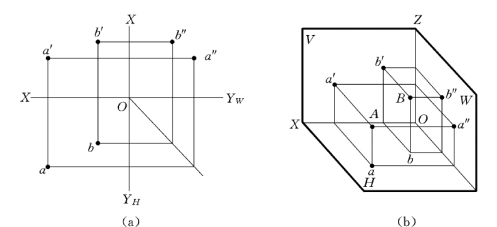
图2-24 两点相对位置
（a）已知点；（b）作图结果
【例2-4】 已知空间点A到三投影面W、V、H 的距离分别为20、10、15，求作点A的三面投影。
解：画投影轴，根据点到投影面的距离与坐标值的对应关系，先作点A （20，10，15）的两面投影：在X轴上量取20，定出点ax，如图2-25 （a）所示；过点ax作OX 轴的垂线，自ax顺OYH方向量取10，作出点A的水平投影a，顺OZ轴方向在垂线上量取15，作出点A的正面投影a′，如图2-25 （b）所示。
根据点的投影规律，作出点A的第三面投影a″。按a′a″⊥OZ，过a′作OZ轴的垂线，交点为az，并量取aza″=aax，得到a″。也可通过45°分角线确定a″，如图2-25 （c）所示。
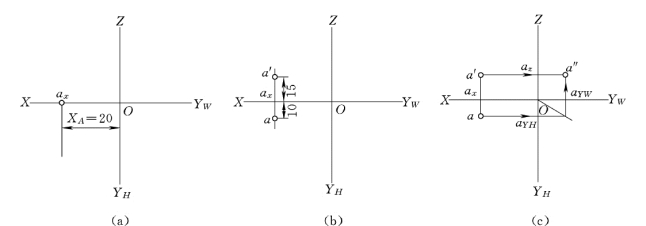
图2-25 点的位置的确定
有关建筑工程制图的文章
- 详细阅读
-
点的三面投影的特性解析详细阅读
由图3-4可以看出，由于投影面相互垂直，三投影线也相互垂直，八个顶点A、a、aY、a"、a'、aX、O、aZ构成正六面体，根据正六面体的性质可以得出点的三面投影的投影特性如下。点的正面投影和水平投影的连线垂直于X轴，即aa'⊥X轴；点的正面投影和侧面投影的连线垂直于Z轴，即a'a"⊥Z轴。例3-1已知点A，求作它的三面投影。......
2023-06-28
-
点的三面投影—画法几何及土木工程制图详细阅读
将三个投影面展开后得到的三面投影图如图2—2b，c。以上所述点的三面投影特性，也正是形体投影图中“长对正、高平齐、宽相等”的理论依据。例2—1如图2—3a所示，已知B点的V投影b′和W投影b″，求其H投影b。......
2023-09-24
-
点的双面投影：理解空间中点的投影方式详细阅读
a称为A 点在H 面上的正投影，即水平投影；a′称为A 点在V 面上的正投影，即正面投影。让V 面不动，把H 面向下转动90°，把V、H 两面投影体系展开，可得展开后点的两面投影，如图2-19 所示。在投影图中，点用小圆圈表示。图2-19点的两面投影显然，有了点的两面投影图，点在空间的位置能被唯一确定。综上所述可总结出点的两面投影的投影规律。点与其投影的连线垂直投影轴。空间点到V 面的距离等于水平投影到OX 轴的距离。......
2023-06-22
-
求解环面上F点的H投影和W投影详细阅读
例5—4已知环面上F点的V投影f′，求作F点的H投影和W投影。解作图步骤如图5—15所示：由于f′可见，F点一定在前半个外环面上。在V投影中，过f′作水平线与外环面的投影轮廓线相交，交点间的长度即为辅助圆的直径；在H投影中作出辅助圆的实形，由F在此圆上定出f，再作出（f″）；图5—15环面上取点因F点在上半环面上，故f可见；又因F点在右半个外环面上，故（f″）不可见。......
2023-09-24
-
钢结构工程识图与施工技巧：三面正投影规律详细阅读
图1-54 三个投影面的展开投影面展开后，形体的水平投影和正面投影在X轴方向均反映形体的长度，其位置应左右对正。这三个关系即为三面正投影的投影规律。三面投影图与各方位之间的关系：1）V面图反映物体的上、下和左、右的关系。......
2023-08-22
-
点的透视投影-画法几何及土木工程制图详细阅读
1）点的透视投影仍然为一点点的透视就是过该点的视线与画面的交点。A点的透视A°与其基透视a°的连线A°a°，其长度称为A点的透视高度，它是点A的实际高度Aa的透视，一般情况下不与实际高度相等。图8—5点的透视作图......
2023-09-24
-
三面投影图的绘制方法与应用详细阅读
这种关系常称为三面投影图的投影规律，简称三等规律。图2-16三面投影面2.2.2.3三面投影图的对应关系1.度量对应关系三面投影图是在物体安放位置不变的情况下，从三个不同方向投影所得到的，它们共同表达同一物体，因此它们之间存在着紧密的关系。......
2023-06-22
相关推荐