2-19一等腰直角△ABC，AC为斜边，顶点B在直线NC上，完成其两面投影。2-20已知菱形ABCD的对角线BD的投影和另一对角线端点的水平面投影a，试完成菱形的投影图。2-25完成下列平面图形的第三投影，并求作出属于平面上的点K的另两个投影，并填空。2-26作图判断点A或直线AB是否属于给定的平面。2-34过已知点A作一直线AB，使其平行于已知平面△DEF。2-36求作直线与平面的交点K，并判断可见性。......
2023-06-15
点、直线、平面的正投影特点
【摘要】：图2-9正投影的类似性2.2.1.4重合性两个或两个以上的点、线、面具有同一投影时，称为重合，这种投影性质称为正投影的重合性，如图2-10所示。
2.2.1.1 全等性
空间直线、平面平行于投影面，其正投影分别反映实长和实形，这种性质称为正投影的全等性。
从图2-7中可看出：直线AB平行于H 面，其正投影ab=AB，直线投影反映实长；平面ABCD平行于H 面，其正投影abcd=ABCD，即平面的形状、大小不变，平面投影反映实形。
2.2.1.2 积聚性
空间直线、平面垂直于投影面时，在该投影面上的正投影分别成为一个点和一条直线，这种性质称为正投影的积聚性，如图2-8所示。
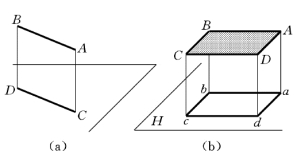
图2-7 正投影的全等性
图2-8 正投影的积聚性
2.2.1.3 类似性
点的正投影仍然是点，直线的正投影一般仍是直线，平面的正投影仍然保留其空间几何形状，这种性质称为正投影的类似性。
如图2-9所示，通过空间点A向投影面H （H 表示该投影面为水平面）引一条铅垂线，该铅垂线（即正投影中的投射线）与投影面H 相交于一点a，a就是空间点A 在H 面上的正投影，显然点的正投影仍然是一个点[见图2-9 （a）]；空间直线段AB与投影面H 倾斜，AB在H 面上的正投影是ab，显然ab仍然是直线，但投影长度小于直线原长[见图2-9 （b）]；空间四边形平面ABCD与投影面H 倾斜，平面在H 面上的正投影为abcd，显然平面的正投影仍然为四边形平面，但投影图形的面积小于空间平面的面积，[见图2-9]。
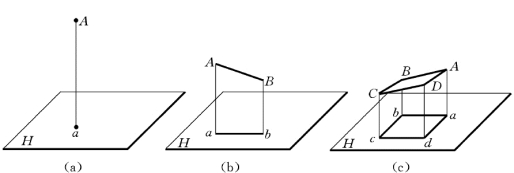
图2-9 正投影的类似性
2.2.1.4 重合性
两个或两个以上的点、线、面具有同一投影时，称为重合，这种投影性质称为正投影的重合性，如图2-10所示。
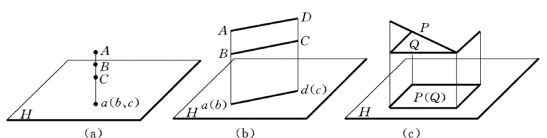
图2-10 正投影的重合性
2.2.1.5 从属性
若点在直线上，则点的投影必在直线的投影上；点在平面内，则点的投影必然在平面的投影上。
2.2.1.6 定比性
直线上两线段长度之比等于该两线段投影的长度之比。两平行线段的长度之比等于它们的投影长度之比。AC∶CB=ac∶cb，如图2-11所示。
以上6种性质，虽以正投影为例讲解，但并非正投影所特有，其实也适用于平行投影。
有关建筑工程制图的文章
- 详细阅读
-
点、直线、平面的投影学习指南详细阅读
本章的地位及特点本章介绍正投影图的基本知识，包括点的投影规律、各种位置直线的投影特性及不同相对位置两直线的投影特性、各种位置平面投影特性，以及点、线、面之间的从属关系，直线与平面的平行和相交关系等。正投影是平行投影的特例，因此平行投影的基本性质是建立正投影的基础。第2章介绍了工程中表示物体的常用方法，本章从点的投影开始，逐步深入地讨论用于表达物体正投影的方法。......
2023-06-28
-
平面内点与直线的关系详细阅读
图2-52平面上的直线的投影规律2.5.3.2平面内与投影面平行的直线凡在平面内平行于某一投影面的直线，称为投影面的平行线，可分为以下三种情况。平面上与投影面倾角最大的直线称为最大斜度线。......
2023-06-22
-
各位置平面投影的特点详细阅读
特殊位置平面又分为投影面垂直面和投影面平行面两种，特殊位置平面的投影特性如下。例3-13如图3-37所示，已知平面的正面投影和侧面投影，求作水平投影。侧垂面的水平投影与正面投影有类似性。表3-5立体上的投影面平行面续表3.一般位置平面的投影特性相对三个投影面都倾斜的平面称为一般位置平面，如图3-38所示，由于它相对三个投影面都倾斜，所以它的三个投影都不反映实形，但具有类似性。......
2023-06-28
-
直线的标高投影解析详细阅读
图7-2直线的标高投影为了更好的了解这两种表示方法，我们先来关注以下两个问题。以直线的标高投影为一条直角边，另一条直角边为直线两端点的高差，则斜边为实长，高差所对内角为直线对基准面的倾角α，如图7-3所示。图7-4定比分割原理求直线的整数标高7.2.2.2直线的坡度和平距直线上任意两点的高差与其水平距离之比称为该直线的坡度。......
2023-06-22
- 详细阅读
-
直线投影检测算法的分析介绍详细阅读
直线投影法是一种基于边界的角点检测算法，其核心思想就是把角点定义在目标的轮廓线上，先分割图像，抽取目标边界的Freeman链码，将方向改变程度较大的点标记为角点。设L为目标区域边界，其局部连续链码可表示为Ljs={aj-s+1 aj-s+2…Ljs在x和y方向的投影，即在链码7和1的方向的投影为式中，ai7，ai1的值由方向码ai的值确定，见表4-1。......
2023-06-28
-
直线的辅助投影：换面法详细阅读
一般来说，作直线的辅助投影主要要解决以下三个基本作图问题。图3-23将一般位置直线变为投影面平行线a1'b1'与X1轴的夹角即为AB对H面的倾角α。图3-25一般位置直线变为投影面垂直线......
2023-06-28
相关推荐