以功率为依据兼顾效率的选择策略

2023-06-22 理论教育版权反馈

【摘要】：如果计入这些损耗，就可得到超级电容器的效率，这在进行超级电容器组单体数量计算时必须考虑。举例来说，图9-6分别给出了一个参数为2600F/2.5V/0.7mΩ的超级电容器在恒流和恒功率条件下的充放电效率曲线。可见，器件的实际性能与厂商标称的有很大差距，因此，在进行超级电容器组的容量设计时，必须考虑由器件内部串联阻抗所导致的效率问题。无论如何，考虑效率时就会导致计算所得器件数量的增加，同时也限制了超级电容器组端电压的变化范围。

正如前文所分析的等效电路模型，超级电容器内部含有一个串联电阻，这意味着在充放电过程中会发生内部损耗。如果计入这些损耗，就可得到超级电容器的效率，这在进行超级电容器组单体数量计算时必须考虑。

举例来说，图9-6分别给出了一个参数为2600F/2.5V/0.7mΩ的超级电容器在恒流和恒功率条件下的充放电效率曲线。图中放电系数d设为50%。不过，即使充放电电流和功率不是恒定值的，也可以参考这个曲线。

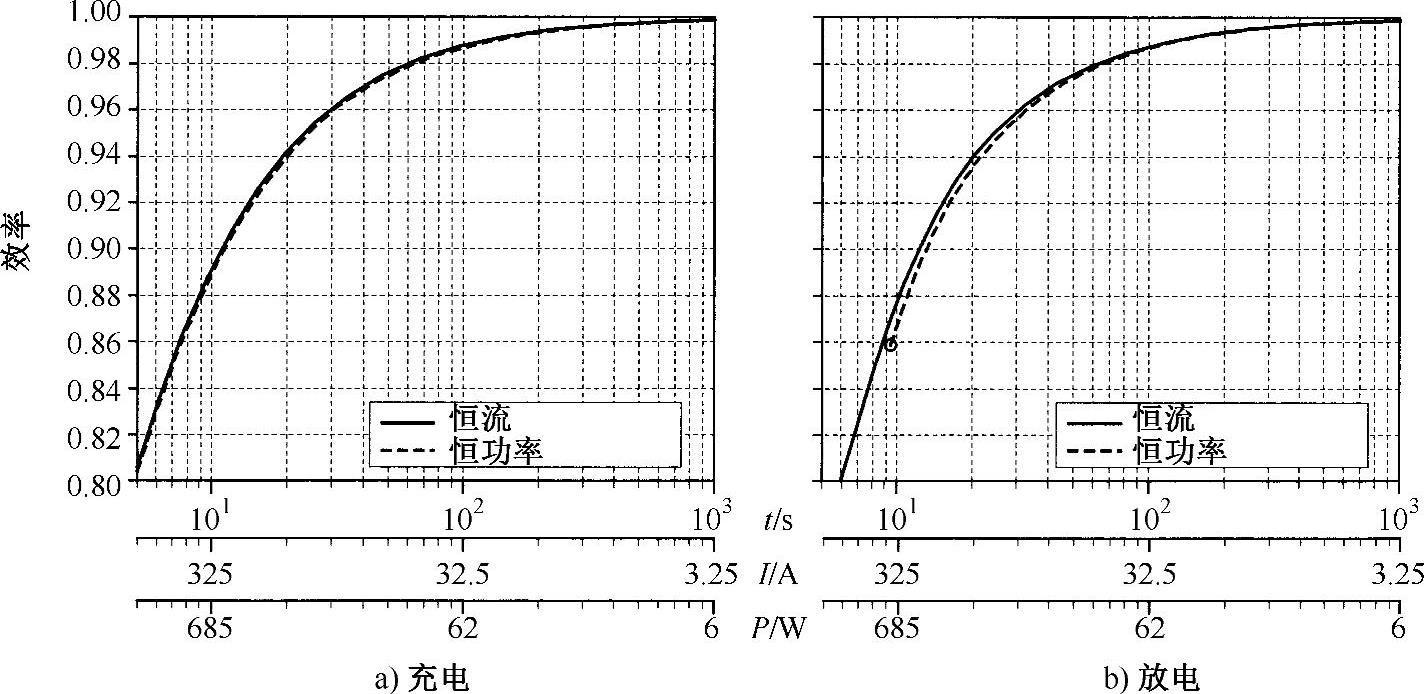
图9-6 超级电容器的效率（2600F/2.5V/0.7mΩ，d=50%）

尽管超级电容器的串联阻抗很小（0.7mΩ），但要使效率大于90%，充电时必须将电流或功率限制在一定的值之下，放电时也是如此。

也就是说，充电时电流需限制在297A以下，或者功率限制在604W以下，才可以得到90%的效率。放电时的条件更加严格一些，电流不得超过267A，功率不得超过423W。

如果我们以允许的最低效率为约束，可以推算出器件的功率密度，由保证器件获得90%效率的放电功率（423W）与器件的质量（0.525kg）之比得到。由此，本例中器件的功率密度为806W/kg，但是厂商给出的却为4300W/kg。

可见，器件的实际性能与厂商标称的有很大差距，因此，在进行超级电容器组的容量设计时，必须考虑由器件内部串联阻抗所导致的效率问题。

图9-7给出了一个考虑效率的超级电容器组容量设计案例，该组超级电容器要求以30kW的功率提供170kJ的能量，单体器件的参数为350F/2.5V/3.2mΩ。

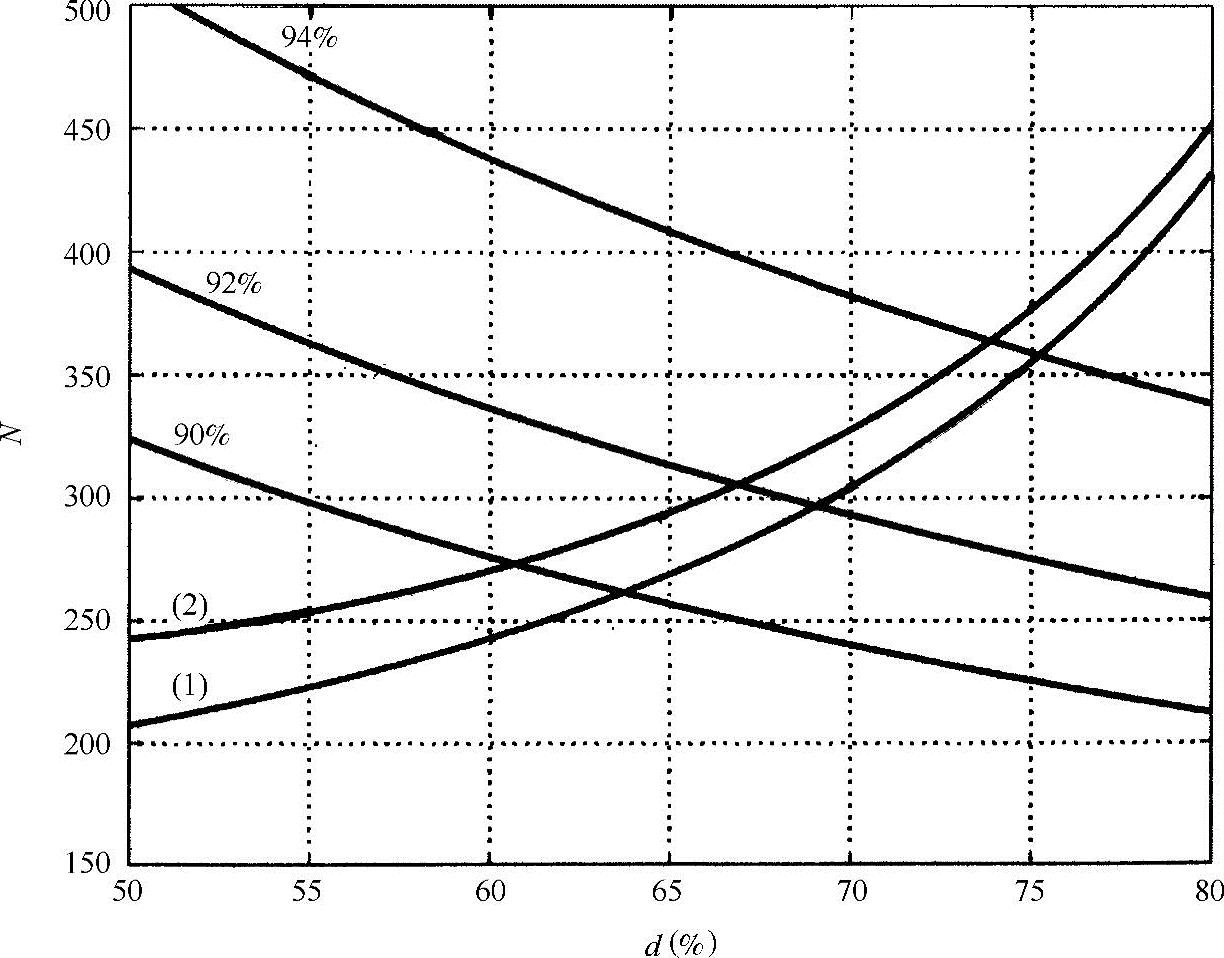
图9-7 考虑效率的超级电容器组容量设计案例

如果不考虑效率，所需器件的数量可以由式（9-6）直接计算出来。如果储能量已知，不同的放电系数d计算出的器件数量也不唯一。假定放电系数d的取值范围是50%～80%，可以得到图9-7中的曲线（1），它给出了一系列的可能选择。

图9-7中也给出了30kW功率而不同效率（90%、92%和94%）下的器件数量选择曲线。从图中可以看出，超级电容器组的效率随着器件数量增加而增大，也随着放电系数增加而增大。

最后，图9-7中的曲线（2）给出了为满足170kJ储能量需求并考虑效率条件下的一系列选择。当效率接近1（N很大，d接近100%）时，该曲线接近理想曲线。无论如何，考虑效率时就会导致计算所得器件数量的增加，同时也限制了超级电容器组端电压的变化范围。最终，器件数量是由曲线（2）（计及效率的能量选择依据）与等效率（功率选择依据）曲线的交点确定的。

在本例中，170kJ/30kW的储能需求对应的设计方案为N=270，d=60.8%，效率90%，或者N=365，d=73.8%，效率74%。

以功率为依据兼顾效率的选择策略

相关推荐