接触器6种特性参数中，影响较大的几项介绍如下。4）和短路保护电器的协调配合接触器和短路保护电器的协调配合试验应由制造厂进行。5）额定工作制接触器有4种标准工作制，具体如下。断续周期工作制时的负载因数标准值为15%、25%、40%和60%。电气控制回路有电流种类、额定频率、额定控制电路电压Uc和额定控制电源电压Us等参数。在多数情况下，这2个电压是一致的。......
2023-06-30
电气模型的主要参数分析
【摘要】：图9-3 超级电容器的等效电路模型电容值C0是超级电容器的主要参数，该值相当于由式（9-1）所定义的两个双电层电容的串联，厂商可以提供这个参数。这个值主要与隔膜的导电性有关，也受电解质所含杂质的影响。所用超级电容器为1500F/2.7V，其实际性能表现与模型吻合。这种现象可以用等效电路模型中的可变电容Cu说明，该电容值为电压u的函数。其值大小部分取决于电极中沉积在金属板上的多孔材料的性能，但主要还是由电解质的离子导电性决定的。
超级电容器通常有两种建模方法，即使用等效电路建模和使用阻抗频谱建模。等效电路建模法的好处在于可以直接将之前定义的参数与实际器件联系起来。而且，还可以将超级电容器的建模过程与实际运行情况直接联系起来，这一点我们将稍后解释（主要是超级电容器组的容量计算与效率分析）。
图9-3给出了超级电容器的等效电路模型，也是最为常用的一个模型[ZUB 00]。
图9-3 超级电容器的等效电路模型
电容值C0是超级电容器的主要参数，该值相当于由式（9-1）所定义的两个双电层电容的串联，厂商可以提供这个参数。
但是，超级电容器电容值的测量结果表明该值并非常数，而是两个双电层端电压的函数，也就是电容器端电压Uc的函数。超级电容器的电容值取决于端电压的原因是与电解质内存在的两个扩散层有关，而每个扩散层都与各自临近的双电层直接接触。扩散层的特征包括体积的大小、阴离子的密度、阳离子的密度，以及电解质的温度。此外，双电层引出端子的电位差与扩散层也有关系，会直接影响扩散层的体积。每个扩散层都有一个电容值，该值与其体积成反比。当超级电容器的端电压增加，扩散层的体积相应减小，并导致其电容值增加。这种现象可以用等效电路模型中的可变电容Cu说明，该电容值为电压u的函数。
实际上，超级电容器的电容值C可以由以下关系定义：
C=C0+Cu，Cu=Ku （9-2）
式中，C0是由两个双电层决定的基本电容值；u是两个双电层的端电压；K是电容值Cu的可变常数。对于某些超级电容器来说，处于最大电压（如2.5V）时，电容值Cu可以达到基本电容值C0的25%。
图9-3中，Rs为超级电容器的串联电阻。其值大小部分取决于电极中沉积在金属板上的多孔材料的性能，但主要还是由电解质的离子导电性决定的。实际上，图9-2中对超级电容器电动势的分析表明，在其充放电阶段（图9-2所示为充电阶段），电解质内会出现一个电压降。当电容器处于放置状态时，电解质内的电压降应该为零，但前提条件是不考虑扩散层的相关作用。串联电阻Rs的值一般在0.5～100mΩ之间，生产商可以提供这个参数。
图9-3中，Rf决定了超级电容器的漏电流，这个漏电流比蓄电池的漏电流要大一些。这个值主要与隔膜的导电性有关，也受电解质所含杂质的影响。当电容器充电超过最高允许电压（电解质的分解电压，主要是由多孔材料和电解质界面上发生的氧化还原反应引起）时，阻抗Rf将减小。Rf通常为500Ω～100kΩ，生产商一般不会给出这个值的大小，而是会提供一个最大电压下漏电流的数据，一般为40μA～10mA。
除了以上给出的超级电容器主要参数，图9-3所示的等效电路模型增加了一系列并联的RC单元（r1c1，…，rncn）。这些单元反映了电荷的再分配现象或者介电张弛过程，其时间常数通常是几秒至几个小时，甚至更长。这种电荷的再分配意味着，由于活性炭超高的孔隙率，存储的电荷由电极的容易接近区域向受限区域转移。因此，在超级电容器的快速充电阶段，电极上的电荷呈现不均匀的分布。当充电完毕，电荷在电极上得以自由移动，经过多个时间常数后，最终呈现一个均匀分布。
图9-4所示为超级电容器在给定的充/放电电流条件下，端电压Uc的变化过程。所用超级电容器为1500F/2.7V，其实际性能表现与模型吻合。
对超级电容器进行恒电流充电和放电，图9-4a给出了电容值与端电压的依赖关系。与曲线（1）相比，图中的电压并非线性增加。不仅如此，图中曲线（2）表明，由于串联阻抗Rs的存在，当充电停止后，超级电容器端电压Uc会出现一个突降。
图9-4b给出了超级电容器的一个完整的充/放电循环。当充电完成，以及由串联电阻引起的电压下降阶段之后，端电压还是出现了明显的下降，其原因不是漏电流，而由张弛现象引起的：电荷在两个电极上自由移动以实现均匀分布的过程导致了一定的电压降，但这个电压降不产生能量损耗。电容器放电之后也会出现这种现象，即使放电至电流为零，因张弛现象也会引起电压的上升。
生产商一般不会提供与张弛现象有关的参数，即使它们很有用。不论超级电容器的充电过程是在几分钟还是几小时内完成，因张弛现象导致电容器实际存储的能量比按其标称电容值测算的更多。不过，这些额外的电容很难利用，尤其是当超级电容器以分钟级的时间常数循环时。因此，与张弛电容有关的储能量一般不予以考虑。
实际上，在图9-3所示的等效电路模型中，通常可以不采用RC张弛电路。
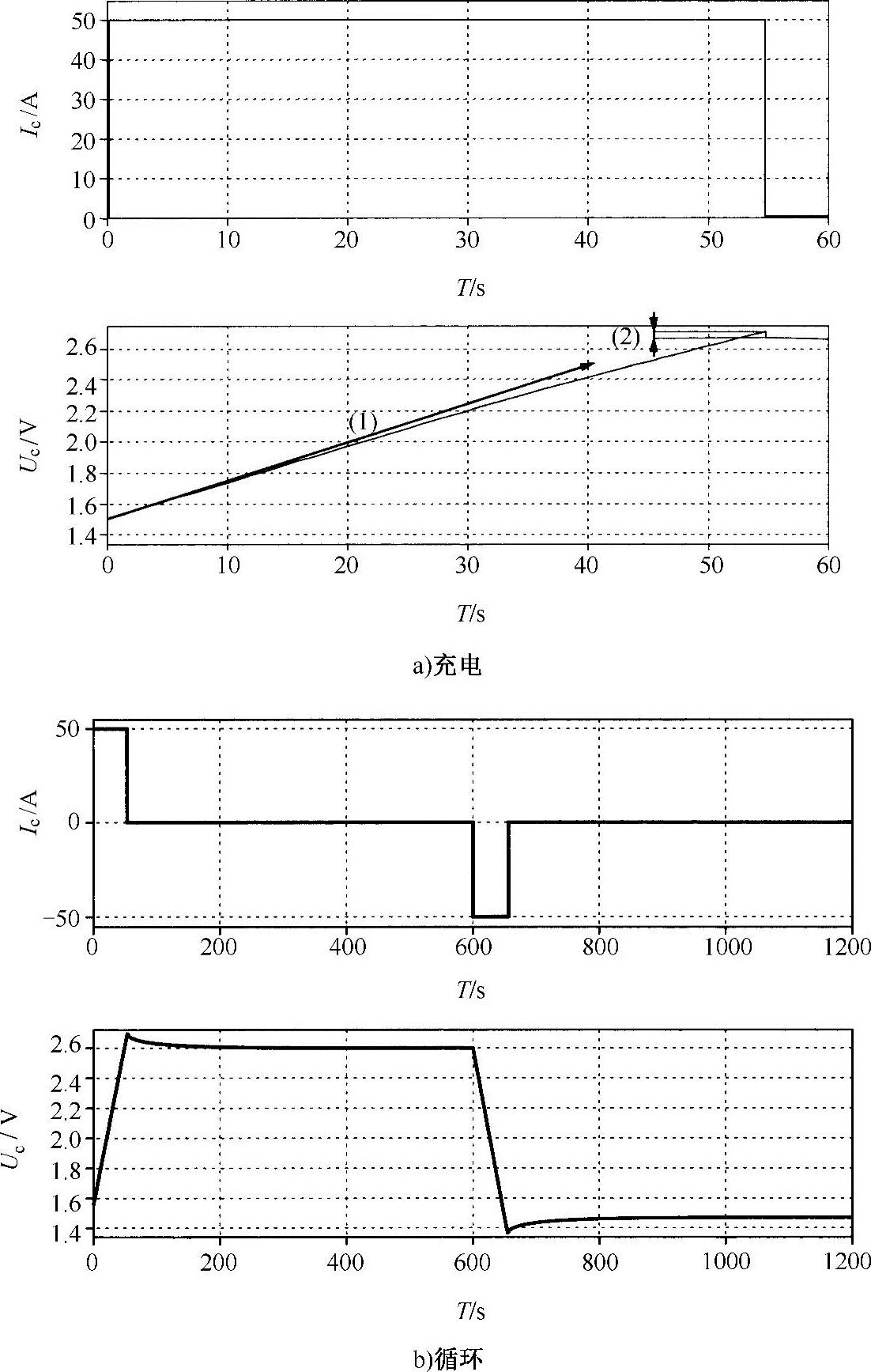
图9-4 超级电容器的充电与放电过程
有关储能技术及应用的文章
- 详细阅读
-
电气火灾原因分析实例详细阅读
造成电气火灾原因很多，但电流产生的热量和火花或电弧是引发火灾的直接原因。发生短路时，线路中的电流增加为正常时的几倍甚至几十倍，使设备温度急剧上升，大大超过允许范围。如果温度达到可燃物的自燃点，即引起燃烧，从而导致火灾。接触部分是发生过热的一个重点部位，易造成局部发热、烧毁。电气设备或线路过热的部分原因如图6-27所示。事故火花是线路或设备发生故障时出现的。......
2023-08-18
-
光耦合器的主要参数分析详细阅读
光耦合器的主要参数有电流传输比CTR、绝缘电压VDC、最大正向电流IFM、反向击穿电压VCEO、饱和压降VCES、暗电流IR。电流传输比CTR是光耦合器的重要参数，在接收管的输出保持不变时，它的输出电流Io与输入电流Ii之比就是传输比，CTR=Io/Ii×100%。图2-11 NEC-2501光耦合器如PC817的传输比为80%～160%，4N30为100%～5000%。......
2023-06-25
-
热和电气特性分析与优化详细阅读
如前所述，大多数LED具有保护功能，避免在电压达10kV或20kV的直接或反向静电放电情况下受到损坏。从热的角度看，LED具有以下特性：1）结和热沉之间的热阻为Rj-s，目前LED的Rj-s一般在5～15K/W，而多芯片LED的热阻低于5K/W；2）正向电压温度系数的单位是V/℃；3）最大结温；4）额定工作模式下的环境空气温度的最大范围。在5.3节中已经解释过最后一个特性非常依赖于热阻Rj-s，但也依赖于总热阻Rj-a。......
2023-06-15
-
电气安全：触电事故规律分析详细阅读
为防止触电事故，应当了解触电事故的规律。根据对触电事故的分析，从触电事故的发生率统计上看，可找到以下规律。应当指出，在专业电工中，情况是相反的，即高压触电事故比低压触电事故多。应当注意，很多触电事故都不是由单一原因引起的，而是由两个及两个以上的原因造成的。在一定的条件下，触电事故的规律也会发生一定的变化。因此，应当在实践中不断分析和总结触电事故的规律，为做好电气安全工作积累经验。......
2023-06-15
-
仿真模型的建立及分析结果详细阅读
图3-25 三角形隶属度函数模糊控制规则是模糊控制的核心，因此，如何建立模糊控制规则成为一个十分关键的问题。根据表3-3所示参数，由式可得D0=0.24；由式可得x0=[0.11573600]T；由式可得图3-28 模糊控制器输出曲线图3-28 模糊控制器输出曲线图3-29 有源电力滤波器整体仿真模型表3-3 仿真参数图3-29 有源电力滤波器整体仿真模型表3-3 仿真参数取正定矩阵取正定矩阵根据实验取定根据实验取定具体仿真结果如下：1）图3-30所示为无滤波器的情况下电网电流波形。......
2023-06-23
-
水文模型的运行与结果分析详细阅读
本研究模拟了1971年到2000年这30年的水文过程，将模拟得到的逐日径流量与实测值进行比较，比较结果如表2所示。然而，模型模拟的低流量水文变量值低于实测值。随后进行了未来气候情景下的水文模型，在对结果的分析中考虑了前面提到的模型的不足。同样地，在模型应用之前，先用空间和时间尺度上插值生成的降水量数据对模型进行了率定和验证。......
2023-06-24
-
耦合模型和非耦合模型的计算成果对比分析详细阅读
图11.11降压结束时水平截面主应力等值线图表11.2耦合非耦合模型计算应力和位移特征值（最大值）比较高压压水引起岩体发生较大位移量的范围约为3.0m，远远小于渗流应力耦合作用模型条件下13m的范围。图11.12为试验区特征铅直剖面上的第三有效主应力等值分布图。由图11.12可知，按流固耦合模型计算得到的应力场分布形态与非耦合模型计算得到的应力场分布形态有显著的差别。......
2023-06-28
相关推荐