岸滩侧蚀数值模拟的关键技术

2023-06-21 理论教育版权反馈

【摘要】：由此实现了由岸滩坍塌引起边坡后退过程的模拟。图6.2-4垂向网格跟踪示意图6.2.2.3 垂向网格跟踪技术应用——岸滩侧蚀沿垂向差异特征及其水动力响应采用连续弯道对岸滩侧蚀沿垂向的差异特征及其水动力响应进行概化模拟分析。

6.2.2.1 局部网格自适应技术

在应用水沙模型对岸滩侧蚀进行模拟时，岸滩崩塌宽度并不一定正好与崩塌处计算网格宽度一致，这就使网格对边岸的准确拟合变得困难。因此，一般的固定网格系统很难准确地处理这种动态的变化过程，不能实时反映边岸变形对水沙输运的影响。采用动网格技术虽能准确地拟合边岸的变化过程，但是需要实时生成网格，特别是在边界复杂时，网格的生成，尤其是正交网格的实时生成存在较大困难。此外，大范围新、旧网格之间的频繁插值也会给计算带来一定的额外误差。

鉴于目前存在的一些不足，本研究基于非正交网格提出局部网格自适应技术对崩岸过程进行跟踪，其基本思路为：在整个大计算域内生成网格，在模拟过程中，仅对发生崩岸附近的网格进行移动，使其能够准确地跟踪边岸位置，同时其余网格位置不变。这样做既能较为准确地拟合崩岸后的岸坡位置，以实时反映边岸变形对水沙输运计算的影响，又无须重新生成整个计算域内的网格，弥补了传统固定网格以及动网格的一些不足，并可提高计算效率。

由三维水沙模型计算得到床面冲刷深度ΔZ及横向冲刷值ΔB，然后根据边坡纵向与横向变形的计算结果，修正边坡的实际形态。初始时刻网格布置如图6.2-3（a）所示，图中节点（i 0，j 0）与（i 0，j 0+1）的连线即为原来的边坡。经过水流冲刷及坍塌后，网格移动情况如图6.2-3（b）所示，此时计算网格节点（i 0，j 0）移动至（i，j）处，从（i 0，j 0+1）展宽至（i，j+1）处，对边坡坡脚及坡顶位置进行了实时跟踪，同时还保留原网格节点（i 0，j 0）与（i 0，j 0+1）的平面位置信息（x 0，y 0）。当坍塌发生后，判断跟踪坡脚的网格节点（i，j）是否已靠近原网格节点（i 0，j 0+1）的位置（ΔY 1＞ΔY 2），若靠近，则节点（i，j）返回原网格节点（i 0，j 0）所在的平面位置，坡脚的网格节点由（i，j+1）进行跟踪，以避免奇异网格的产生，如图6.2-3（c）所示。此时节点（i，j）的冲淤情况则由水流泥沙模型计算来决定，而节点（i，j+1）则处于坡脚位置，需计算ΔZ及ΔB。此时坡顶位置则由节点（i，j+2）进行跟踪，如图6.2-3（d）所示。由此实现了由岸滩坍塌引起边坡后退过程的模拟。

在模拟过程中，采用数组来记录二元结构岸滩上层黏性土层及下层非黏性土层的厚度H u和H d[图6.2-3（d）]，以及上层黏性土层的实际悬空长度ΔW，并由前文所建立的二元结构岸滩坍塌力学模式计算岸滩的失稳过程及相应的坍塌体积。崩塌土体中一部分将以源项形式进入悬沙，剩余部分则均匀分布于坡脚处，对近岸起到掩护作用。

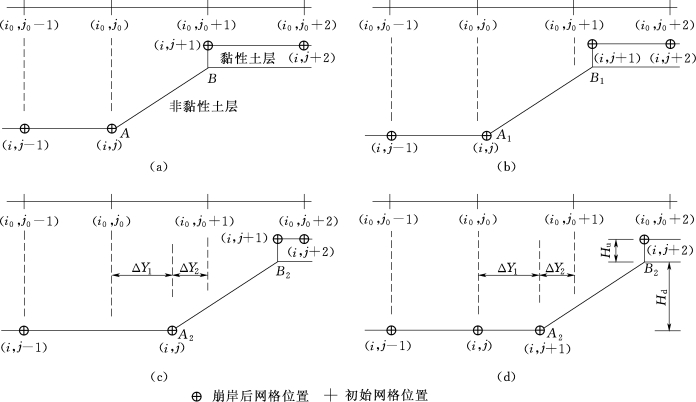
pagenumber_ebook=260,pagenumber_book=237

图6.2-3　二元结构岸滩局部网格自适应技术示意图

6.2.2.2 垂向网格跟踪技术

非均质岸滩（如二元结构）侧蚀模拟过程中，如何实现侧蚀沿垂向差异的拟合与跟踪，是其中一大难点。在应用模型对岸滩侧蚀进行模拟时，岸滩在垂向各点的侧蚀宽度不一致，且往往与该处计算网格宽度也不一致，这就使网格对岸滩侧蚀的准确跟踪变得困难。因此，一般的固定网格系统无法准确地处理这种动态的变化过程，不能实时反映岸滩侧蚀变形对水沙输运的影响。针对目前存在的不足，本研究基于非正交网格提出垂向网格跟踪技术，对岸滩侧蚀过程进行跟踪，其基本思路为：在整个大计算域内生成网格，在模拟过程中，仅对岸滩侧蚀附近的垂向网格进行移动，使其能够准确地跟踪岸滩垂向各点的位置，同时其余网格位置不变。这样做既能较为准确地拟合岸滩侧蚀后的岸坡位置，以实时反映岸滩侧蚀对水沙输运计算的影响，又无须重新生成整个计算域内的网格，弥补了传统固定网格以及动网格在这方面的一些不足。

岸滩侧蚀前形态如图6.2-4中折线ABE所示，BE由初始网格（i+1）描述。模拟过程中，由三维水沙动力学模型计算岸滩侧蚀分布，受岸滩组成沿垂向差异的影响，下部冲蚀多，上部冲刷少，岸滩侧蚀后形态为悬臂式，如图6.2-4中折线AB′C′D′E′所示。此时，侧蚀后的岸滩形态则通过垂向网格跟踪技术对其进行描述：通过移动初始网格（i+1）中相应垂向网格（K 1～K 2）的水平位置，使其与B′C′位置保持重合；通过移动初始网格（i）中相应垂向网格（1～K 1）的水平位置，使其与D′E′的位置保持一致。网格跟踪过程中，采用数组记忆岸滩垂向各点位置与水平相邻网格节点的距离，如图6.2-4中d y 1、d y 2所示，经水流冲刷、岸滩侧蚀后，依据d y 1与d y 2的相互关系来识别、确定和跟踪网格，以避免奇异网格的产生；当d y 1＜d y 2时，岸坡位置由网格（i）跟踪，网格（i+1）保持在原初始网格位置不变；当d y 1＞d y 2时，岸坡位置由网格（i+1）跟踪，网格（i）同样保持在原初始网格位置不变。由此即可实现基于非正交网格的垂向网格跟踪技术对岸滩侧蚀过程的识别与描述。

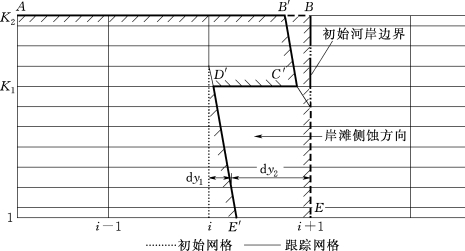
pagenumber_ebook=261,pagenumber_book=238

图6.2-4　垂向网格跟踪示意图

6.2.2.3 垂向网格跟踪技术应用——岸滩侧蚀沿垂向差异特征及其水动力响应

采用连续弯道对岸滩侧蚀沿垂向的差异特征及其水动力响应进行概化模拟分析。连续弯道宽4m，弯顶处8号断面初始断面形态如图6.2-5（a）所示，可冲蚀岸坡设置在左侧凹岸，岸坡上部为黏土（厚0.3m，粒径0.02mm），下部为非黏性沙（粒径0.20mm）。概化模拟过程为强清水冲刷，流量恒定为2.6m3/s，平均流速约为1.2m/s；为分析岸滩侧蚀沿垂向的差异特征及其水动力响应，假定弯道底部不可冲，抗冲层沿图6.2-5（a）所示的1∶5.5斜坡分布。

图6.2-5（彩图7）给出了弯顶处断面岸滩侧蚀过程及其水动力变化特征。由图可见，坡脚沿着抗冲层发生冲刷，底部主流向左侧凹岸偏移，如图6.2-5（b）所示；随着下部非黏性土层的冲刷发展，底部主流进一步偏向凹岸，同时在已有逆时针弯道环流的基础上，于坡脚处出现一顺时针方向（反向）次生流，如图6.2-5（c）所示；上部黏性土层坍塌后，崩塌土体堆积于坡脚处，上部主流明显左偏，下部次生流消失，如图6.2-5（d）所示；随着坡脚堆积体的冲刷搬运，下部主流进一步向凹岸偏移，如图6.2-5（e）所示。如此循环，主流不断向左侧凹岸偏移，致使岸坡持续崩退、河道摆动。

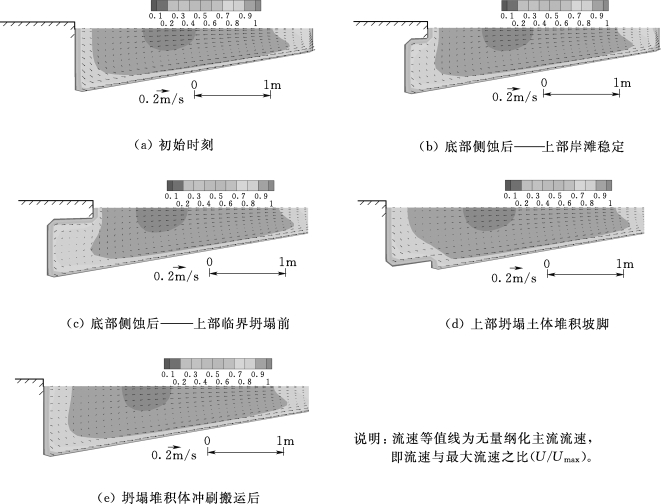
pagenumber_ebook=262,pagenumber_book=239

图6.2-5　岸滩侧蚀过程及其水动力响应特征

由此可见，采用垂向网格跟踪技术，可较好地识别和跟踪河岸侧蚀沿垂向的差异；数值模型可较好地模拟河岸侧蚀过程中三维水流结构的变化特征。应当指出，本研究仅对非均质岸滩侧蚀坍塌过程及其水动力响应进行了概化模拟分析，天然实际岸滩侧蚀机理及形态均十分复杂，还有待进一步深入研究。

岸滩侧蚀数值模拟的关键技术

相关推荐