推移质起动概率分析

推移质起动概率是推移质运动基本规律研究中最具挑战性的问题之一，良好的泥沙起动概率模型将提高推移质输沙率计算的精度。同时，研究推移质起动概率有助于认识三峡水库入库推移质的运动规律，为解决回水变动区的卵砾石碍航问题提供理论基础。本研究采用水槽试验方式来研究推移质起动概率。

3.1.3.1 试验系统

1.试验水槽

试验水槽安装在清华大学水沙科学与水利水电工程国家重点实验室内，如图3.1-17所示，其基本参数及装置如下：

（1）长11m，宽0.25m，高0.25m，整体安装误差为0.2mm。

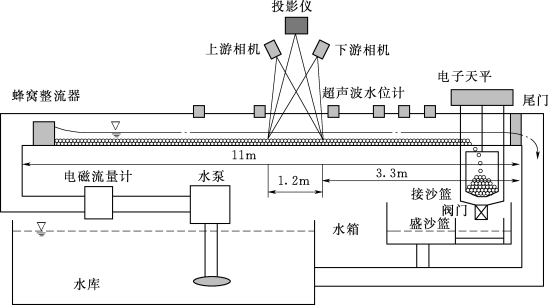
图3.1-17　推移质输沙试验水槽基本参数及装置示意图

（2）变坡循环水槽，可调坡度为0～1.5%。

（3）沿程安装6个超声波水位计，测量精度为0.2mm。

（4）流量通过变频器调整水泵转速调节，流量大小由电磁流量计监测。

（5）水槽上游入水口处安装蜂窝整流器，水槽尾部安装可调尾门，通过调整尾门开度来实现水流均匀流态。

2.接沙系统

推移质接沙系统为推移质试验的重要装置，该系统由电子天平和接沙篮组成，如图3.1-18所示，其中电子天平数据发送频率为1次/s，最大称重30kg，精度0.1g。悬吊在水槽末端沉沙箱内的接沙篮用细钢丝绳连接到电子天平下部的挂钩上，接沙篮下部设开闭闸板，试验过程中关闭闸板，接沙称重，获得推移质输沙重量的累积过程，当接沙篮满载后开启底部闸板，篮内的泥沙快速滑入沉沙箱底部，即刻关闭闸板；在这数秒钟的操作过程中，沉沙箱内的水沙总体积没有变化，不影响水槽内的水流运动。其后，打开沉沙箱底阀门即可将泥沙下泄至纱网制成的盛沙篮内，盛沙篮放置在一个与水库相连、水位齐平的小水箱内，沉沙箱内的水沙进入盛沙篮后水体从纱网排出，始终保持小水箱内的水面与水库的水面齐平；缓慢提起盛沙篮完成一次取沙。由于取沙过程水库内水位高程不变，水泵出水流量恒定，实现推移质输沙试验无限制地连续进行，实验效率大幅提高。特别是，在清水冲刷下河床粗化试验中，该接沙系统能够实现分时段接沙，这对研究河床粗化过程中推移质输沙级配随时间的变化规律起到了至关重要的作用。

图3.1-18　推移质试验接沙系统布置图

3.均匀推移质平衡输沙试验

在推移质平衡输沙试验中，一般要在水槽上游安装加沙机，试验过程中水深沿程不变，并且下游断面的输沙率与上游加沙率相等，这种做法需要反复调整加沙率，较为繁琐。实际操作中，只要水槽足够长，无需安装加沙机也可开展短时间内的推移质平衡输沙试验，操作步骤如下：

（1）在水槽末端的接沙篮入口前端固定安装一个挡沙板以控制床面基准高程，在水槽内沿程铺满与挡沙板高度相等的试验沙，本试验的铺沙厚度为27mm；开启水泵，利用变频器逐渐将水流流量增加至设定流量，缓慢调整尾门以满足水位沿程相等，水流将逐渐进入均匀流状态（图3.1-19）。

图3.1-19　水槽末端挡沙板布置图

（2）每组平衡输沙试验均在二维均匀流条件下进行（宽深比B/H＞5），试验过程中要确保距离尾门1～2m处所设置的3个超声水位计（A、B、C三处，位于水槽纵轴线上）的水位差小于0.5mm（水面有一定的波动），并记录自由水面平均高程，如图3.1-20所示。大量试验表明，只要上游泥沙补给充分，尾门开度调整合适，试验过程中A、B、C三处的自由水面高程一致，电子天平输出的推移质泥沙累积质量也随时间线性增加。

图3.1-20　推移质试验过程中水深及输沙量测量

（3）在试验过程中，根据天平实时输出的数据，利用Matlab平台实时计算推移质单宽输沙率g b[kg/（m·s）]，以检验输沙率是否稳定。当推移质单宽输沙率为直线的斜率时，即达到平衡状态，如图3.1-21所示；实际操作中，平衡输沙试验持续20min以上即可停止。

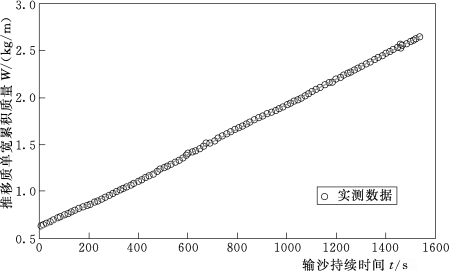
图3.1-21　推移质试验的单宽输沙率计算方法

注：试验工况为比降S=0.0115，流量Q=9.19m3/h，水深H=20mm，水槽宽度B=0.25m，试验沙粒径d=3.24mm，单宽输沙率g b=0.0013kg/ms，从而计算出水流强度Θ=0.043以及输沙强度Ф=0.00068。

（4）关闭水泵，待水槽内水流泄空后，利用超声水位计测量床面高程，试验过程中的自由水面高程与床面高程之差即为试验水深H：

式中：ZsA、ZsB和Z sC为试验过程中A、B、C三处的自由水面高程（基本相等）；ZbA、ZbB和Z bC为A、B、C三处的河床高程。

所有平衡输沙试验中宽深比B/H∈[5.8，21.7]，按照均匀流公式[1]计算摩阻流速u*：

式中：S为水槽坡度。

图3.1-22　推移质试验中不同输沙条件下的自由水面情况

由图3.1-22（a）可见，在低强度输沙时（Θ＜0.067），由于水槽末端固定安装挡沙板的原因，A、B、C三处的自由水面和床面都较为平整，超声水位计可正常工作。由图3.1-22（b）可见，在中高强度输沙试验时，水面波动严重且床面出现沙波，超声水位计无法正常工作，此时要借助钢板尺在水槽边壁处实时测量水深，试验水深取测量值的平均值。

（5）将接沙篮内的泥沙取出倒入水槽上游端，用铺沙板刮平床面。变换试验工况（包括增大流量和调整水槽坡度）进行下一组次的平衡输沙试验。

上述5个步骤是较为严格的推移质平衡输沙试验操作流程，经过上百次试验的摸索，没有必要在每组次试验完毕后关闭水泵、测量床面高程、取出泥沙、重新铺沙、重新开启水泵等耗时环节，即可连续进行推移质平衡输沙试验。

4.高速摄影测量系统

在清华大学水沙科学与水利水电工程国家重点实验室的封闭槽道中开展推移质输沙过程测量，封闭槽道长6.4m、宽0.25m、高0.2m，由上、下游不锈钢过渡段和中部观测段连接而成；观测段四壁均为高强度玻璃，以便于开展光学测量实验，观测段底板比上下游底板低5cm，以填充试验沙。槽道前端为可升降水箱，最大可提升高度为6m，用于提供驱动水流的压力水头，水箱与槽道入口之间依次连接供水软管和渐变截面段，以保证水流平稳过渡。槽道出口依次连接渐变截面段和排水软管，保证水流平稳流出，排水软管上依次安装电磁流量计和蝶形电动阀门，用于自动测量和控制流量。试验开始前，在观测段底板平整铺设长2m、厚5cm的均匀天然沙，中值粒径d 50为1mm，密度ρs为2650kg/m3，对应的临界起动Shields数Θc=0.036[2]。定义x轴沿水流方向，y轴沿水深竖直向上，坐标原点位于床面中心线。

试验观测断面设置在观测段中部，仪器布置示意如图3.1-23。水槽上方竖直向下安装1号高速相机用于拍摄床沙图像，该相机CCD大小为640×480像素、满画幅拍摄帧频200Hz。为提高采样频率，试验时采用640×300像素的局部拍摄模式，使采样频率增大至315Hz，拍摄分辨率R为7.7像素/mm。1号高速相机上游侧倾斜安装照明用LED灯，用于均匀照亮床面待测区域的泥沙颗粒。在进行起动试验时，为测量水流摩阻流速，在测量区域下游使用高频粒子图像测速（TR-PIV）系统测量水槽中垂面内的二维流场，PIV系统所使用的连续激光器安装在水槽上方，2号高速相机安装在水槽侧面，测量范围为5cm×10cm，PIV系统的详细参数和性能可参见文献[3]。

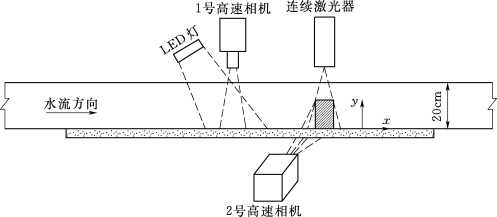
图3.1-23　高速摄影系统试验仪器布置图

（1）测量区域照明方法。

在泥沙起动试验中，为了增加测量区域亮度，使高速相机可在极短的曝光时间内捕获清晰的床沙图像，通常需要在摄像时使用额外光源照亮测量区域。在刘春嵘[3]等的试验中，水槽侧面安装连续激光器，激光片光与床面水平相切以照亮床沙。显然，这种照明方式仅适用于床面极为平整的情况，更为关键的是，由于激光片光主要照亮床面上暴露度较大的凸起颗粒，而这些颗粒更容易在水流作用下发生运动，因此，以被激光片光照亮的泥沙作为统计样本，根据样本中发生运动的泥沙比例计算起动概率，将导致测量结果比实际结果偏大。为避免在图像采集时出现系统性偏差，合理的床沙照明方式应为俯视床面的均匀立体照明。

（2）图像处理方法。

利用高速摄影方法测量起动概率的关键在于根据床沙图像统计运动泥沙的数量，因此，通常需要在拍照时使用较高的分辨率，使单颗泥沙在图片中的直径大于3个像素；同时，为避免粒子成像时发生拖尾现象，相机拍摄时应设置较短的曝光时间。图3.1-24为高速相机实际拍摄的一张床沙图片，由于成像分辨率高、曝光时间短，图片整体亮度较暗、信噪比较低。为增加图像的清晰度和对比度，避免背景照明不均匀、杂质、气泡等对识别结果产生影响，首先对原始图像进行顶帽变换、对比度线性拉伸和高速滤波处理，处理后效果如图3.1-25所示。

图3.1-24　高速相机原始床沙图像

图3.1-25　经处理后的床沙图像

为了从连续两张图片中提取出运动泥沙，一种方法是从第一帧图片中标识出所有泥沙颗粒的位置和范围，再将每个颗粒图像与第二帧图片中对应位置的图像进行相关计算，根据相关系数的大小判断颗粒是否发生位移，若已运动，则在一定搜索区域内进行移动相关计算，根据相关峰值的位置求出颗粒位移（刘春嵘等，2008）。上述方法的缺陷主要包括：从第一帧图片中识别出的泥沙颗粒往往暴露度大，根据这些样本统计起动概率容易产生偏差；对每个颗粒进行判读需要耗费大量的计算资源，计算效率较低；该类方法仅适用于粒径较大且起动泥沙数较少的情况，当起动泥沙数量较多或颗粒粒径较小时，颗粒之间的辨识度急剧降低，容易发生误匹配现象。

为克服上述缺陷，一种更为常用的方法是将两帧图片相减，根据图像灰度的变化判读泥沙是否发生运动，这种方法的理论依据是颗粒运动导致初始位置和当前位置的灰度均发生改变。在泥沙起动试验中，由于运动泥沙暴露度大、距光源近，其对应的灰度值一般比静止泥沙大，当泥沙发生运动后，其初始位置的灰度变小而当前位置的灰度增大，当利用第二帧图片减去第一帧图片时，初始位置的灰度为负，当前位置的灰度为正。分析本试验实际拍摄的图片时发现，运动颗粒既可能比静止颗粒亮，也可能比静止颗粒暗，但前者出现概率极低，在统计分析时不会对测量结果产生影响。图3.1-26（彩图2）展示了一张典型的灰度差分布图，图中成对出现的正负峰值清晰标识了运动泥沙的初始位置和当前位置。

以图3.1-26中数值为正或负的部分为分析对象，经二值化处理即可求得运动泥沙的位置和面积。本试验以数值为负的部分为分析对象，二值化阈值经反复测试后统一选择为-18。为尽量减少测量噪声对结果的影响，对二值化结果进行形态学开处理，以剔除尺寸小于4×4像素的伪颗粒。图3.1-27展示了根据图3.1-26所示灰度差提取出的运动泥沙分布，其中，一个白色连通区域代表一颗运动泥沙。根据运动泥沙的数量N、中值粒径D、拍摄分辨率R以及测量区域对应的图片面积A m，可计算出瞬时运动比例为

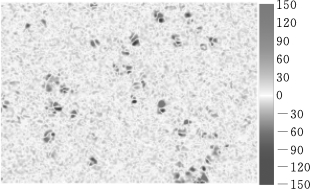
图3.1-26　连续两帧床沙图片的灰度差

图3.1-27　提取出的运动床沙

需要指出的是，在细颗粒泥沙起动试验中，泥沙颗粒容易成群起动，若按泥沙数量计算运动比例会产生较大误差，此时可按识别出的运动泥沙的面积进行计算。

（3）相机帧频设定标准。

理论分析中的起动概率是与时间无关的瞬时量，但在实际测量过程中，总需要一定的时间间隔来检测泥沙颗粒的运动。对基于高速摄影的泥沙起动测量技术，为了使实测值逼近真实值，两帧图像之间的时间间隔Δt应足够小，以满足捕捉泥沙颗粒每一次起动的要求。

根据Nikora[4]等提出的低输沙强度推移质运动概念模型，推移质运动主要有局部、中间和全局三种时间尺度。局部时间尺度T l是指泥沙颗粒连续两次与床面发生碰撞的时间间隔；中间时间尺度T m是指泥沙颗粒连续两次处于静止状态的时间间隔，由于泥沙从起动到止动的过程中可能多次与床面发生碰撞，中间时间尺度一般包含多个局部尺度；以此类推，全局时间尺度T g是指包含有多个中间尺度的时间间隔，如图3.1-28所示。根据上述模型，只有当两帧图像之间的拍摄间隔Δt＜T m时，相机才可能捕捉到泥沙颗粒的每一次起动。因此，高速摄像时相机的最小帧频应满足以下条件：

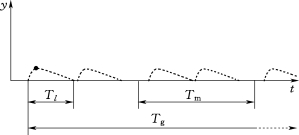
图3.1-28　推移质运动概念模型

已有文献对局部时间尺度有较多可参考结果，但少有关于推移质运动中间尺度的研究报道。Nikora等在利用实测资料分析不同尺度条件下推移质的扩散规律时发现，中间时间尺度和全局时间尺度的分界点约为。基于此，定义推移质运动的中间时间尺度为

在实际测量中，拍摄帧频除了应满足式（3.1-13）要求外，还应保证泥沙颗粒在两帧图片之间的位移适中，以准确识别颗粒运动及其位移。

3.1.3.2 泥沙起动概率试验结果

1.起动概率预报模型检验

为提供泥沙起动概率数据来检验不同起动概率模型，选取经典的推移质实测输沙率数据（221组），这些可靠性较高的数据被国内外诸多研究人员分析及使用过。

推移质输沙试验发现不同强度的水流将会塑造不同的床面形态，低强度水流冲刷时，床面将形成条带结构，高强度水流冲刷时，床面将形成沙波。图3.1-29（彩图3）为利用三维地形测量系统所重构的水槽输沙试验中的三维床面形态。

图3.1-29　水槽试验中被水流冲刷后的床面形态（d=1.0～1.5mm）

由于床面形态的存在，沙粒切应力需要校正，沙粒切应力校正时可能会引入人为主观因素（如Einstein[5]校正方法、Engelund[6]校正方法等）。由于粗颗粒泥沙组成的河床在低强度水流冲刷下较为平坦，此时不需要进行沙粒切应力校正，为此，本试验计算泥沙起动概率时，仅使用试验中粗颗粒泥沙的99组平衡输沙率数据。

综上所述，共有363组推移质平衡输沙率实测数据参与了泥沙起动概率P的计算，将计算结果P-Θ点绘于图3.1-30。为检验不同泥沙起动概率模型的性能，选取了著名的Einstein（1950）起动概率公式及其修正公式，同时也选取了最有代表性的Fredsøe和Deigaard[7]公式，将上述泥沙起动概率公式一起绘入图3.1-30中。

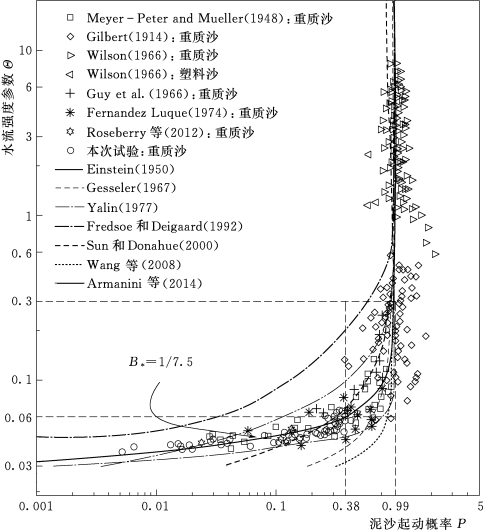
图3.1-30　泥沙颗粒起动概率理论公式与本研究试验所提供的起动概率数据对比

由图3.1-30可见，相对于用本研究收集资料所计算的泥沙起动概率数据，Fredsøe和Deigaard（1992）公式计算值偏小，Wang et al.[8]（2008）公式在低强度水流条件下有所偏大，Yalin[9]（1977）和Armanini et al.[10]（2014）公式基本能预测起动概率变化趋势，而备受后人质疑的Einstein[5]起动概率公式却与本研究提供的数据最为吻合[注：Einstein在原著中已说明其起动概率公式P中的系数可由推移质输沙率率定，公式中原系数B*=1/6.06，后被钱宁[11]更正为B*=1/7.0，本研究将其更新为B*=1/7.5，这样Einstein（1950）公式与本计算数据的吻合程度较使用上述系数略有提高，见表3.1-9]。

一些研究者认为Einstein起动概率公式存在三大缺陷：

其一，关于水流上举力分布的问题。由于脉动流速符合高斯分布，所以水流上举力应该符合χ2分布[12]。事实上，王兴奎等[13]（1993）通过试验发现瞬时水流上举力基本符合正态分布，所以这点不应该成为一个缺陷。

其二，关于起动概率积分区域的问题。部分研究者认为只有方向向上的上举力才能对泥沙起动有贡献，故起动概率积分区域不应该包含方向向下的水流上举力。事实上，当诸如Yalin（1977）和Wang等（2008）公式中采用与Einstein（1950）公式相同的参数B*和η0时，修正公式的起动概率计算结果与Einstein（1950）公式的计算结果基本相等，所以积分区域也不应该成为一个缺陷。低强度输沙试验表明，床面上不少泥沙颗粒处于上下振动状态，目前还难以否认方向向下的水流上举力对泥沙起动同样具有一定的贡献。

其三，关于泥沙颗粒受力问题。Laursen[14]以及Sun和Donahue[15]认为Einstein只考虑的水流上举力F L对泥沙起动的贡献，而忽略了水流推力F D的作用。实际上，无论采用滚动、滑动或者跳跃起动模式，尽管所获得的Θc的表达式不同，由于相关参数（如C D、C L、ψ、α等）的取值并不统一，若采用合适的参数，所得到的泥沙起动条件可以完全相等，同样的，无论采用何种起动模式，同样可以获得与Einstein（1950）公式中的相等的B*和η0，所以泥沙颗粒受力问题也不应该成为一个缺陷。

综上所述，本研究认为Einstein（1950）起动概率本身没有重大缺陷。此外，Einstein（1950）推移质平衡输沙率公式难以预报高强度输沙率的原因也不是因为起动概率P的问题，而是因为Einstein（1950）在建立推移质输沙模型时将泥沙起动的随机性推广到任意水流条件下。泥沙起动的随机性只有在Θcmin和Θcmax之间有效，当水流强度参数Θ超出Θcmax之后，泥沙起动则为一个必然事件。图3.1-30表明，当Θ＞0.3，泥沙起动概率P已基本接近于1，这种水流状态下的推移质输沙率使用确定性研究方法较为合理。

表3.1-9　Einstein（1950）起动概率公式及其修正公式

注 Einstein（1950）公式中的系数B*=1/7.0被更新为B*=1/7.5。

2.高速摄影测量结果

利用高速摄影方法能够获取推移质起动概率。本研究在5m压力水头工况下，测量了4种不同流量条件下的起动概率，随着流量的增大，泥沙起动现象从个别起动逐渐变为少量起动。为避免沙纹等床面结构对水流产生影响，未在更大流量条件下继续开展起动试验。在泥沙起动试验中，由于观测的床面区域有限，每组试验均需要长历时采集样本，将统计样本的期望值作为该水流条件下的起动概率。在本研究试验中，每组试验均连续采集40000帧图片用于计算起动概率。

表3.1-10　推移质水槽试验主要试验参数统计表

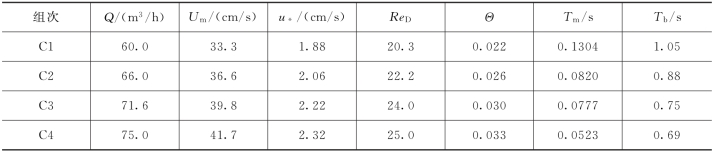
注 Q为流量，U m为断面平均流速，摩阻流速u*根据PIV实测平均流速剖面按对数律进行拟合（Jiménez，2004）；颗粒雷诺数Re D=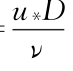，水流强度参数Θ=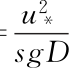，g为重力加速度，s=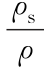-1为泥沙水下比重，ρs为泥沙密度，ρ为水密度，ν为水的运动黏性系数；T m为推移质运动的中间时间尺度，T b为水流紊动猝发的平均周期。

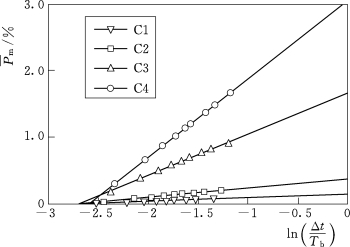
图3.1-31　推移质实测平均运动比例随拍摄间隔变化规律

利用每组试验中连续拍摄的40000张床沙图片，分别将间隔0、1、2、3、4、5、7、9、14张图片的两张图片选为一对，计算出拍摄间隔Δt分别为1s/315、2s/315、3s/315、4s/315、5s/315、6s/315、8s/315、10s/315、15s/315时对应的瞬时运动比例，进而求得不同拍摄间隔条件下的平均运动比例。图3.1-31在半对数坐标系下点绘了平均运动比例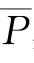m随无量纲拍摄间隔Δt/T b的变化趋势，图中实线为利用模型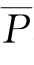m=a ln（Δt/T m）+b对实测点进行拟合的结果，其中，a、b为待定系数。在利用高速摄影方法进行床沙运动测量时，当拍摄间隔较大时，单颗泥沙在拍摄间隔内无论运动几次，在两张图片中均表现为空间位置的改变，实测运动比例将随着Δt的增大而趋于饱和，因此，图中实测运动比例随Δt对数增长的趋势与实际相符，表明本研究测量方法可靠。

根据图3.1-31中的拟合结果，可计算出不同水流条件下的起动概率。图3.1-32点绘了实测起动概率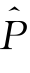m随相对水流强度参数Θ/Θc的变化趋势，其中，临界起动Shields数Θc按Cao等[2]提出的显示方法计算。受实验条件限制，本研究未能测得Θ/Θc≥1条件下的起动概率，这就增加了推求Θ/Θc=1时的临界起动概率的难度，为了尽量合理地通过外延方法推求临界起动概率，分别用二次多项式、指数函数和幂函数对实测点进行拟合，其中，二次多项式拟合时限制Θ/Θc＞0.6时为单调递增函数，拟合结果及其对应的拟合优度R 2如下：

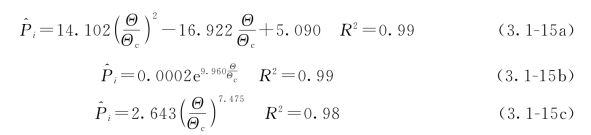
图3.1-32（a）和（b）分别在笛卡尔坐标系和半对数坐标系绘制了起动概率拟合曲线随Θ/Θc变化趋势，图中结果表明，尽管式（3.1-15）中每个拟合公式对应的拟合优度R 2均接近1，但根据不同公式外延计算出的临界起动概率差异较大。根据图3.1-32（b）中拟合曲线变化趋势以及Shields数的定义可知，若起动概率与相对水流强度之间的关系满足式[3.1-15（b）]及式[3.1-15（c）]，则摩阻流速u*增大至临界摩阻流速u*c的1.16倍或1.28倍时，起动概率将增大至100%，与实际情况不符。因此，根据式[3.1-15（a）]计算临界起动概率，计算结果为2.27%，与窦国仁[16]根据理论分析结果定义的少量起动概率2.28%接近。

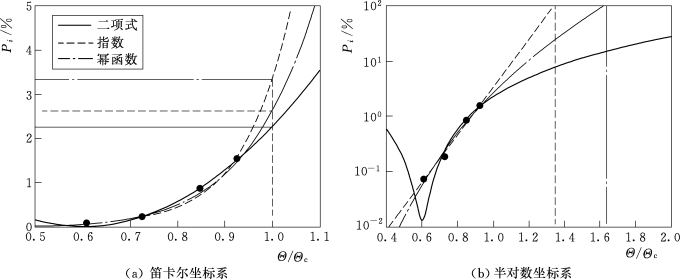
图3.1-32　起动概率随相对水流强度参数的变化趋势