推求防洪限制水位的逆时序计算法，仍是依据G5.2中介绍的调洪计算原理，所不同的是将当年允许最高水位Z允作为起始条件，其相应的泄流量和蓄水量作为第一个时段末的值q2、V2，逆时序调节计算求逐时段初的q1、V1，进而得到防洪限制水位。具体方法可采用列表试算法、半图解法。
由水量平衡方程和蓄泄方程可得逆时序调节计算的半图解法的公式为
通常式（G8.4）表示为关系线q—（V/Δt-q/2），称为辅助曲线。
以控制泄流与自由泄流相结合的泄流方式为例，介绍逆时序调洪计算的方法步骤如下：
（1）确定调洪计算的时段Δt，计算并绘制辅助曲线q—（V/Δt-q/2）。具体方法与顺时序调洪计算相似。
（2）确定调洪计算的起始条件。在当年允许最高洪水位已定时，闸门全开的最大溢洪水头Hm＝Z允-Z堰，即当年允许最高洪水位和溢洪道堰顶高程之差。当淹没系数、侧收缩系数均等于1时，利用溢洪道出流公式（G5.3），由最大溢洪水头Hm可以求得水库的最大下泄流量qm，即
其中
式中 M1——也称为流量系数；
其他符号含义同前。
因此，当年允许最高洪水位相应的蓄水量及qm，则分别为最后一个时段（也为逆时序计算的第一个时段）末的值V2、q2。
（3）逆时序逐时段调洪计算。由q2＝qm，在入流过程线Q—t的退水段，找到qm＝Q时刻，记tm，如图G8.4所示。若tm在时段分界处，则由公式（G8.3）可计算V1/Δtq1/2，并由此值查辅助曲线q—（V/Δt-q/2），得该时段初的值q1。若tm不在时段分界处，则应采用试算法，求时段初的值q1、V1。
将q1作为前一时段末的q2，用半图解法依次可求得逐时段初的流量q1，直至某一时刻的泄流量等于涨水段的某一入流量Q时为止，如图G8.4中的b点。但往往b点不在时段Δt的分界点上，因此需用试算法或由Q—t线和q—t线的交点得出该点流量。当b点的泄流量qb求得以后，即可由溢洪道的泄流量公式反求出相应堰顶水头Hb，进而求得防洪限制水位Z限＝Z堰＋Hb，或利用Z—q关系查得Z限。
图G8.4 某水库入流与出流曲线
【例G8.1】 某水库溢洪道设有闸门，下游无防洪要求。水库防洪设计标准为1%，相应设计洪水位为61.72m，校核标准为0.2%，校核洪水位为62.50m；工程已按规划设计时的标准运行。其他有关资料如下：
（1）水库容积关系见表G8.1。
表G8.1 水位—容积关系表
（2）溢洪道堰顶高程57.48m，堰宽B＝35m，流量系数M1＝
＝1.77。
（3）经分析汛期分为前汛期（主汛期）6月1日至8月15日，后汛期（尾汛期）8月16日至9月30日。后汛期p＝1%的设计洪水过程线见表G8.2中的第（1）、（2）栏。
图G8.5 某水库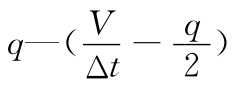
辅助曲线
试推求后汛期防洪限制水位。
计算过程如下：
（1）确定调洪计算时段Δt＝1h，从堰顶以上开始，对某一水位计算q、（V/Δt-q/2）（限于篇幅，计算过程不一一列出），然后绘制辅助曲线q—（V/Δt-q/2），如图G8.5所示，其中V为堰顶以上库容。
（2）确定调洪计算的起始条件。对于本例，设计条件下，当年允许最高洪水位为设计洪水位，闸门全开的最大溢洪水头Hm＝Z允-Z堰＝61.72-57.48＝4.24（m），由式（G8.5）求得：
根据qm查辅助曲线，得V2/Δt-q2/2＝3140m3/s。
（3）逆时序逐时段调洪计算。由q2＝qm，在入流过程线Q—t的退水段，找到qm≈Q的时刻为7h，由式（G8.3）可计算V1/Δt-q1/2＝V2/Δt-q2/2-
＝3140-620＋541＝3061（m3/s），由此值查辅助曲线q—（V/Δt-q/2），得q1＝525m3/s。依次逐时段计算结果见表G8.2。相应于时间1h的泄流量大于入流量，显然是不合理的，说明在时段1h～tb应控制泄流，q＝Q。由Q—t线和q—t线的交点得出tb点流量qb＝220m3/s，如图G8.4所示。进而求得
Z限＝Z堰＋Hb＝57.48＋［220/（1.77×35）］2/3＝59.81（m）
表G8.2 逆时序半图解法调洪计算表
需要指出，当水库年允许的最高水位低于设计条件下的校核洪水位时，求得的当年主汛期的防洪限制水位有可能低于堰顶高程，此种情况下，则需结合流域暴雨特性和水库堰顶高程以下的泄流能力分析其可行性，特别是要分析发生连续洪水时，防洪限制水位与堰顶高程之间的蓄水量的泄放时间应不大于发生连续洪水的时间间隔，且应留有余地。
有关工程水文及水利计算的文章
DocOfClassReduce，循环遍历输出，当概率更大时就更新tempClass和tempProbably；Step4.3 GetPriorProbably，计算先验概率，利用该静态函数计算每个类的文档在总类中占的比例；Step4.4 GetConditionProbably，计算条件概率。Step5利用测试文档的真实类别，计算评价指标Step5.1 OriginalDocOfClassMap，读写原本的文档分类，得到文档分类的类别；Reduce，计算得出初始情况下各个类有哪些文档。Step5.3 GetEvaluation，利用所选评价指标评价算法。......
2023-11-08
粒子群算法和其他的进化算法类似， 也是根据群体对环境的适应度， 将个体选择更好的区域进行移动。在标准的粒子群算法中， 粒子的速度和位置的变化可由公式(6-1)和公式(6-2)计算获得。标准的粒子群算法流程分为以下几个步骤：初始化种群。需要随机产生群体中所有粒子的初始速度和位置， 确定粒子的pbest 和gbest。......
2023-06-20
Spark MLlib中的K-means算法使用Map分布式读取数据集，并存储在内存里。计算时，用Map键值对表示随机挑选出来的k个聚类中心，Spark的驱动器节点负责把数据发送到各个工作节点，以实现具体的计算任务。Spark MLlib不同于传统的机器学习工具，它提供了简单易用的API，特别是Spark能够高效地处理大数据，并且在迭代计算时具有较强的优势。......
2023-11-21
在上位机将控制算法传输到控制卡后，控制卡会将控制算法信息暂存到控制算法缓冲区，并不会立即对控制算法进行解析。所以，控制算法的解析必须选择合适的时机。本系统中将控制算法的解析操作放在本周期的控制算法运算结束后执行，这样不会对本周期内的控制算法运行产生影响，新的控制算法将在下一周期得到执行。上位机下发给控制卡的控制算法包含控制算法的操作信息、回路信息和回路中各功能模块信息。......
2023-11-22
开源飞控为我们提供了丰富的研究、实践、学习资料。为了平衡硬件与算法实践难度，本小节会以Multiwii开源飞控为例，挑选2.3版本控制器实现的部分代码与大家一同分析。完整代码或其他开源算法中的实现过程，大家可以通过互联网找到。在控制器设计中往往会涉及三个方面：误差的获取，基于误差的算法实现，控制信号的生成和输出。代码中errorGyroI[axis]+error体现了上一小节中积分运算的程序实现方式。......
2023-07-05
式表示的空间滤波器称为逆滤波器。除此之外，逆滤波器还可用计算全息图来制造。采用逆滤波器消模糊又称为无限制的消模糊，它无法解决系统噪声的影响。如果采用加性噪声模型，则式和式应表示为当应用式所示的逆滤波器进行空间滤波处理时，输出平面上的复振幅为上式表明，由于模糊系统的传递函数H存在着一系列零点和弱的高频分量，第二项将变得很大，以至淹没有用的第一项，致使原始物体像得不到恢复。......
2023-11-23
本节根据MSAA的特征模型和渐进式比对算法构件的交互模型，利用Apla语言的高抽象性、对泛型及ADT的良好支持以及易于正确性验证等优点，来形式化实现多序列比对算法构件。prog构件该构件为ADT类型HMSAA中的泛型子程序，根据传入不同类型的计算比对步骤进行渐进式比对。result_op构件该构件为ADT类型，泛型子程序multiAlign_op在多序列比对结果的基础上，对结果进行格式化输出。......
2023-10-25
对于正弦波的负半周，可以用倒相技术或负值三角波来进行调制。图4-26单极性SPWM脉宽调制波形如图4-26用单相正弦波全波整流电压信号U s与单向三角形载波U c交截，再通过倒相得到功率开关驱动信号，或直接用参考正弦波与单向三角形载波交截产生功率开关驱动信号。......
2023-07-02
相关推荐