首页理论教育水库调洪计算原理简介

水库调洪计算原理简介

2023-06-21 理论教育版权反馈

【摘要】：调洪计算的原理就是根据起始条件，逐时段连续求解水量平衡方程和水库的蓄泄方程，从而求得水库出流过程q—t。若水库设有水电站，且发生洪水时能够运行，则泄洪能力中还应计入水轮机过水流量q电，其值一般可按水轮机过水能力的2/3～4/5计入。综上所述，水库调洪计算的原理，就是由已知的Δt、Q1、Q2、q1、V1、联解式和式，求得q2、V2。

洪水波在水库中运动时，其流态属于缓变不恒定流，沿程的水力要素（水位、流量、流速等）都是随时间变化的，其运动规律可用圣维南方程组进行描述，该方程组由连续方程和运动方程构成，但目前尚无直接求解的办法，故水库调洪计算中，常做一定的简化，采用水库的水量平衡方程和水库的蓄泄方程。调洪计算的原理就是根据起始条件，逐时段连续求解水量平衡方程和水库的蓄泄方程，从而求得水库出流过程q—t。

1.水库水量平衡方程

如图G5.2所示，对调洪过程中任意时段Δt（Δt＝t2-t1），可得水量平衡方程

图G5.2　水库水量平衡示意图

即

式中　Q1，Q2——时段初、末的入库流量，m3/s；

q1，q2——时段初、末的出库流量，m3/s；

V1，V2——时段初、末的水库蓄水量，m3；

Δt——计算时段，s，其长短选择视入库洪水过程的变化情况而定，陡涨陡落的，t取短些；反之取长些；

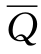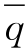，——时段平均入库、出库流量，m3/s；

ΔV——时段Δt的水库蓄水变量，m3。

2.水库蓄泄方程或蓄泄曲线

水库的蓄泄方程反映的是水库蓄水量V与泄洪能力q之间的单值关系。所谓泄洪能力是指水库在某一蓄水量V条件下，泄洪建筑物闸门全开或无闸门时的泄流量q。蓄泄方程可表示为

式（G5.2）常以曲线形式表示，称为蓄泄曲线或泄洪能力曲线，记q—V。

对于溢洪道，其泄流能力q溢按堰流公式计算

式中　ε、σs、m——堰的侧收缩系数、淹没系数（自由出流时，σs＝1）和流量系数，其值可查水力学手册或通过模型试验确定；

B——溢洪道宽度，m；

h——堰顶水头，m。

对于泄洪洞，其泄流能力q洞可按有压管流计算

式中　μ——泄洪洞的流量系数，其值可查水力学手册或通过模型试验确定；

ω——泄洪洞洞口面积，m2；

h——计算水头，当淹没出流时，h为上、下游水位差，m，非淹没出流时h为泄洪洞出口处的洞心水头，m。

若水库设有水电站，且发生洪水时能够运行，则泄洪能力中还应计入水轮机过水流量q电，其值一般可按水轮机过水能力的2/3～4/5计入。船闸、灌溉渠首等建筑物，一般过水能力不大，通常不考虑其参与泄洪。

水库蓄泄曲线q—V绘制方法为：假定若干个库水位Z，按泄洪建筑物出流公式计算各水位对应的各个出流量，水库泄洪能力的总和q＝q溢＋q洞＋q电；由各水位Z利用库容曲线Z—V可查得对应的各个库容V，根据q、V关系值，可点绘q—V曲线。

综上所述，水库调洪计算的原理，就是由已知的Δt、Q1、Q2、q1、V1、联解式（G5.1）和式（G5.2），求得q2、V2。依时序逐时段递推计算，可得水库出流过程。

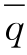，——时段平均入库、出库流量，m3/s；

ΔV——时段Δt的水库蓄水变量，m3。

2.水库蓄泄方程或蓄泄曲线

水库的蓄泄方程反映的是水库蓄水量V与泄洪能力q之间的单值关系。所谓泄洪能力是指水库在某一蓄水量V条件下，泄洪建筑物闸门全开或无闸门时的泄流量q。蓄泄方程可表示为

式（G5.2）常以曲线形式表示，称为蓄泄曲线或泄洪能力曲线，记q—V。

对于溢洪道，其泄流能力q溢按堰流公式计算

式中　ε、σs、m——堰的侧收缩系数、淹没系数（自由出流时，σs＝1）和流量系数，其值可查水力学手册或通过模型试验确定；

B——溢洪道宽度，m；

h——堰顶水头，m。

对于泄洪洞，其泄流能力q洞可按有压管流计算

式中　μ——泄洪洞的流量系数，其值可查水力学手册或通过模型试验确定；

ω——泄洪洞洞口面积，m2；

h——计算水头，当淹没出流时，h为上、下游水位差，m，非淹没出流时h为泄洪洞出口处的洞心水头，m。

若水库设有水电站，且发生洪水时能够运行，则泄洪能力中还应计入水轮机过水流量q电，其值一般可按水轮机过水能力的2/3～4/5计入。船闸、灌溉渠首等建筑物，一般过水能力不大，通常不考虑其参与泄洪。

水库蓄泄曲线q—V绘制方法为：假定若干个库水位Z，按泄洪建筑物出流公式计算各水位对应的各个出流量，水库泄洪能力的总和q＝q溢＋q洞＋q电；由各水位Z利用库容曲线Z—V可查得对应的各个库容V，根据q、V关系值，可点绘q—V曲线。

综上所述，水库调洪计算的原理，就是由已知的Δt、Q1、Q2、q1、V1、联解式（G5.1）和式（G5.2），求得q2、V2。依时序逐时段递推计算，可得水库出流过程。