用数学统计法分析数据

2023-06-21 理论教育版权反馈

【摘要】：数理统计法有合成总库容法、直接总库容法和随机模拟法等。某多年调节水库，已知多年平均年径流量＝6000万m3、Cv＝0.6、Cs＝2Cv，年供水量W用＝4500万m3，p设＝85%。已知Cv＝0.3、Cs＝3Cv，α＝0.8，p设＝90%，求β多。因为Cs≠2Cv，故需先用式变换参数。当代表年的来水、用水确定后，就可采用年调节兴利调节计算方法确定年库容。在不计损失的基础上，可进一步计入损失。

数理统计法有合成总库容法、直接总库容法和随机模拟法等。以下仅对生产实际中常用的合成总库容法作简要介绍。

由多年调节的含义，多年调节水库的兴利库容Vp具有双重作用，一部分用来调节年际之间的水量，即拦蓄丰水年的余水量，以补充枯水年的年水量不足，设这部分库容为V多，并称其为多年库容；另一部分调节年内来水与用水之间的不均衡性，设这部分库容为V年，并称其为年库容。基于多年调节兴利库容的双重作用，合成总库容法的基本出发点是分别求V多和V年，然后将两者相加得到设计兴利库容。即

1.多年库容的确定

库容系数β多等于多年库容与多年平均年径流量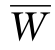之比，即

引入上述相对值后，前苏联水文学学者普列什柯夫应用水量平衡与频率组合原理，于1939年研制了Cs＝2Cv时各种保证率的β多—α—Cv关系图，称之为线解图，如图G4.15所示。该线解图是在假定各年来水相互独立及各年年用水量相同的情况下研究的。

当来水一定时，应用普氏线解图，若α、β多、p设三者中知其二，则能求得另一个。

图G4.15　普列什柯夫线解图

（a）p＝50%；（b）p＝75%；（c）p＝80%；（d）p＝85%；（e）p＝90%；（f）p＝95%

由于多年库容调节丰、枯水年年际之间的水量，所以计算时以年为时段进行水量平衡分析，研究来水、用水、设计保证率、V多四者之间的关系。对于来水，采用皮尔逊Ⅲ型概括为三个统计参数：多年平均年径流量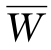、变差系数Cv、偏态系数Cs；用水量和多年库容采用相对值，引入调节系数α和多年库容系数β多。

调节系数α等于设计年用水量与多年平均年径流量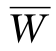之比，即

库容系数β多等于多年库容与多年平均年径流量之比，即

当来水一定时，应用普氏线解图，若α、β多、p设三者中知其二，则能求得另一个。

图G4.15　普列什柯夫线解图

（a）p＝50%；（b）p＝75%；（c）p＝80%；（d）p＝85%；（e）p＝90%；（f）p＝95%

【例G4.8】某多年调节水库，已知多年平均年径流量＝6000万m3、Cv＝0.6、Cs＝2Cv，年供水量W用＝4500万m3，p设＝85%。求多年库容V多。

首先求调节系数α＝＝0.75，然后在p＝85%的线解图中，查出对应于Cv＝0.6、α＝0.75的β多＝0.54。于是，V多＝β多＝0.54×6000＝3240（万m3）。

如对于给定的p设值无图可查，例如p设＝92%，则由相近的两图，即p＝90%和p＝95%，分别求得两个β多，再用直线内插法确定相当于p设＝92%的库容。

线解图是在Cs＝2Cv的情况下绘制的，当Cs≠2Cv时，必须先进行变换，把α、β多、Cv转换成α′、β′多、C′v，然后再查线解图。我国学者张永平研究了转换公式：

其中　a0＝（m-2）/m，m＝Cs/Cv。

【例G4.9】已知Cv＝0.3、Cs＝3Cv，α＝0.8，p设＝90%，求β多。

因为Cs≠2Cv，故需先用式（G4.22）变换参数。由a0＝（m-2）/m＝（3-2）/3＝0.33，得

然后由α′＝0.7、C′v＝0.45，在保证率p设＝90%的图中查得β′多＝0.29，则由式（G4.22）中的β′多式得

β多＝0.29×（1-0.33）＝0.19

强调指出，普氏线解图是在年用水量固定不变的情况下绘制的，若各年的年用水量不同，则不能直接查图，需进行有关处理，可参阅有关文献。

2.年库容的确定

多年库容的计算是以年为计算时段求得的，它用于调节枯水年年用水量的不足，没有考虑年内来水和用水的变化。由于年内来、用水之间存在矛盾，仅有多年库容是不够的。还必须有解决年内来、用水之间矛盾所需的年库容。

年库容的确定，采用代表年法。当代表年的来水、用水确定后，就可采用年调节兴利调节计算方法确定年库容。关于代表年的选择遵循以下原则。

（1）选择年来水量等于年用水量的年份，即完全年调节的年份。其理由是根据多年调节丰水年与枯水年组的随机组合情况，通过分析可以得出，年库容取决于设计枯水年组（决定多年调节兴利库容的枯水年组）前一年丰水年的亏水量，或设计枯水年组第一年（枯水年）的余水量。若选择丰水年，一般说来，枯水期亏水量的大小与年水量有关，年水量越小，枯水期亏水量越大，所需年库容越大，为安全起见，应选年来水量较小的年份，但由于是丰水年，年来水量不应小于年用水量。若选择枯水年，一般说来，年来水量越大，丰水期的余水量也越大，所需年库容越大，为安全起见，应选年来水量较大的年份，但由于是枯水年，年来水量不应超过年用水量。综合上述两方面考虑，选择年来水量恰好等于年用水量年份。

（2）年内分配取多年平均情况。由于年水量的选择已按不利的原则考虑，因而年内分配不再考虑不利的情况。

具体计算时不一定存在正好具备上述条件的代表年，一般可选年来水量最接近年用水量的几个代表年；对各代表年通过同倍比缩放使年来水量等于年用水量；进而采用G4.6节介绍的列表法或简化水量平衡公式法进行兴利调节计算，求出几个年库容，然后取其平均值或略偏大值作为采用的年库容。

在求得的多年库容V多和年库容V年基础上，则可求得多年调节水库的设计兴利库容Vp＝V多＋V年。在不计损失的基础上，可进一步计入损失。

合成总库容法能考虑来水的不同排列，可解决无资料情况下设计兴利库容的推求。但需要指出，水库在实际运用中是不存在截然分开的两部分库容V多和V年的，这是计算中人为划分的，而且将有设计保证率概念的V多与没有设计保证率概念的V年相加所得Vp，其设计保证率概念不明确。

首先求调节系数α＝＝0.75，然后在p＝85%的线解图中，查出对应于Cv＝0.6、α＝0.75的β多＝0.54。于是，V多＝β多＝0.54×6000＝3240（万m3）。