如何计算设计洪峰流量和洪量系列的频率？

G2.2.2.1　特大洪水及其作用

所谓特大洪水，目前还没有一个非常明确的定量标准，通常是指比实测系列中的一般洪水大得多的稀遇洪水，例如模比系数K≥2～3。特大洪水包括调查历史特大洪水（简称历史洪水）和实测洪水中的特大值。

目前，我国各条河流的实测流量资料多数都不长，一般都不超过100年，即使经过插补延后几十年的资料来推算百年一遇、千年一遇等稀遇洪水，难免会存在较大的抽样误差。而且，每当出现一次大洪水后，设计洪水的数据及结果就会产生很大的波动，若以此计算成果作为水工建筑物防洪设计的依据，显然是不可靠的。如果能调查和考证到若干次历史特大洪水加入频率计算，就相当于将原来几十年的实测系列加以延长，这将大大提高资料系列的代表性，增加设计成果的可靠度。例如：我国某河某水库，在1955年规划设计时，仅以20年实测洪峰流量系列计算设计洪水，求得千年一遇洪峰流量Qm＝7500m3/s。其后于1956年发生了特大洪水，洪峰流量Qm＝13100m3/s，超过了原千年一遇洪峰流量。加入该年洪水后按n＝21年重新计算，求得1000年一遇洪峰流量Qm＝25900m3/s，为原设计值的3倍多，可见计算成果很不稳定。若加入1794年、1853年、1917年和1939年等历史洪水，并将1956年的实测洪水与历史洪水放在一起，进行特大值处理，则求得千年一遇洪峰流量Qm＝22600m3/s。紧接着1963年又发生了Qm＝12000m3/s的特大洪水，将它加入系列计算，得到千年一遇的洪峰流量Qm＝23300m3/s，与22600m3/s比较只相差4%。这充分说明考虑历史洪水，并对调查和实测的特大洪水作特大值处理，设计成果也基本趋于稳定。上述计算成果见表G2.5。

表G2.5　某水库不同资料系列设计洪水计算成果表

上述实例充分说明了调查、考证历史上发生的大洪水是提高洪水系列代表性的又一重要、有效的手段。加入洪水特大值，补充了实测资料的不足，起到了延长系列和增加系列代表性的作用，从而减少了抽样误差，使设计值趋于稳定，有效地提高了设计成果的可靠性。

G2.2.2.2　不连序系列

由于特大洪水的出现机会总是比较少的，因而其相应的考证期（调查期）N必然大于实测系列的年数n，而在N-n时期内的各年洪水信息尚不确知。把特大洪水和实测一般洪水加在一起组成的样本系列，在由大到小排队时其序号不连序，中间有空缺的序位，这种样本系列称为不连序系列。不连序系列有三种可能情况，如图G2.2所示。

图G2.2（a）中为实测系列n年以外有调查的历史大洪水QM1，其调查期为N年。

图G2.2（b）中没有调查的历史大洪水，而实测系列中的QM远比一般洪水大，经论证其考证期可延长为N年，将QM放在N年内排位。

图G2.2（c）中既有调查历史大洪水，又有实测的特大值，这种情况比较复杂，关键是要将各特大值的调查考证期考证准确，并弄清排位的次序和范围。

对于不连序的样本系列，其经验频率的计算及统计参数的初估，与连序样本系列有所不同，解决这两个问题通常也称为特大洪水的处理。

图G2.2　特大洪水组成的不连序洪水系列

（a）实测期外有特大洪水；（b）实测期内有特大洪水；（c）实测期内、外均有特大洪水

G2.2.2.3　经验频率的计算

设在调查考证期N年中有特大洪水a个，其中l个发生在n项连序实测系列内。这类不连序系列，目前我国采用的计算方法有以下两种：

（1）分别处理法。即将实测一般洪水样本与特大洪水样本，分别看作是来自同一总体的两个或几个连序随机样本，则各项洪水分别在各自的样本系列内排位计算经验频率。a个特大洪水按式（G2.2）计算经验频率

式中　M——特大洪水排位的序号，M＝1，2，…，a；

N——特大洪水的调查或考证期，即为调查或考证的最远的年份至样本资料最末一年的年数；

pM——特大洪水第M项的经验频率。

同理，实测一般洪水的经验频率按式（G2.3）计算

式中　m——实测洪水排位的序号，m＝l＋1，l＋2，…，n；

n——实测洪水的项数；

pm——实测洪水第m项的经验频率；

l——实测洪水中提出作特大值处理的洪水个数。

（2）统一处理法。即将实测系列和特大值系列都看作是从同一总体中抽取的一个容量为N的不连序样本，各项洪水均在N年内统一计算其经验频率。

对于a个特大洪水，其经验频率仍按式（G2.2）计算，而实测系列中剩余的（n-l）项的经验频率按式（G2.4）计算

（1）矩法。对于不连序系列，矩法公式与连序系列的计算公式有所不同。设调查考证期N年内共有a个特大洪水，其中l个发生在实测系列中，（n-l）项为一般洪水。假定除去特大洪水后的（N-a）年系列的均值和均方差与（n-l）年系列的均值和均方差相等，即，可推导出不连序系列的均值和变差系数Cv的计算公式如下

式中　xj——特大洪水的洪峰流量或洪量，j＝1，2，…，a；

xi——实测一般洪水的洪峰流量或洪量，i＝l＋1，l＋2，l＋3，…，n；

其他符号含义同前。

偏差系数Cs由于抽样误差较大，一般不直接计算，而是参考相似流域分析成果，选用一定的Cs/Cv值作为初始值。

式中　pMa——是N年中末位特大值的经验频率，

其他符号含义同前。

【例G2.1】某站1938～1982年共45年洪水资料，其中1949年洪水比一般洪水大得多，应从实测系列中抽出作特大值处理。另外，通过调查历史洪水资料，得知本站自1903年以来的80年间有两次特大洪水，分别发生在1921年和1903年。经分析考证，可以确定80年以来没有遗漏比1903年更大的洪水，洪水资料见表G2.6，试用两种方法分析计算各次洪水的经验频率，并进行比较。

1.用分别处理法计算

按式（G2.2）和式（G2.3）分别计算洪水特大值系列及实测洪水系列的各项经验频率。1921年洪水Qm＝8540m3/s，在特大值系列中（N＝80年）排第一，则

实测系列中由于将1949年抽出作特大值处理（l＝1），所以排位实际上应从m＝l＋1＝2开始，即1940年洪水经验频率为

2.用统一处理法计算

a个特大值洪水的经验频率仍用式（G2.2）计算，结果与独立样本法相同。（n-l）项实测洪水的经验频率按式（G2.4）计算，1940年洪峰流量的经验频率为

其余各项实测洪水的经验频率可仿此计算，成果列入表G2.6中。

表G2.6　某站洪峰流量系列经验频率分析计算表

由表G2.6中计算结果可以看出，特大洪水的经验频率两种方法计算一致；而实测一般洪水的经验频率两种方法计算结果不同，如1940年洪水（m＝2），分别处理法计算频率为4.35%，统一处理法计算为5.84%，可见第二种方法计算的经验频率比第一种方法计算值大。

研究表明，统一处理法公式更具有理论依据；分别处理法可能出现特大洪水的经验频率与实测洪水的经验频率有“重叠”的不合理现象，即末位几项特大洪水的经验频率大于首几位实测一般洪水的经验频率，但由于其比较简单，因此目前两种方法都在使用。一般来说，分别处理法适用于实测系列代表性较好，而历史洪水排位可能有遗漏的情况；统一处理法适用于在调查考证期N年内为首的各项历史洪水确系连序而无错漏的情况。

G2.2.2.4　洪峰流量与洪量系列频率适线

洪峰流量和不同时段洪量的样本系列的各项经验频率确定后，就可以在频率格纸上点绘经验点，并以此为基础采用适线法推求理论频率曲线，其方法已在X3.6介绍，此处着重对不连序系列统计参数的初估方法、适线的原则等问题进行介绍。

1.统计参数的初估

对于不连序系列统计参数初值的估算方法，常用矩法和三点法。

（1）矩法。对于不连序系列，矩法公式与连序系列的计算公式有所不同。设调查考证期N年内共有a个特大洪水，其中l个发生在实测系列中，（n-l）项为一般洪水。假定除去特大洪水后的（N-a）年系列的均值和均方差与（n-l）年系列的均值和均方差相等，即，可推导出不连序系列的均值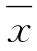和变差系数Cv的计算公式如下

式中　xj——特大洪水的洪峰流量或洪量，j＝1，2，…，a；

xi——实测一般洪水的洪峰流量或洪量，i＝l＋1，l＋2，l＋3，…，n；

其他符号含义同前。

偏差系数Cs由于抽样误差较大，一般不直接计算，而是参考相似流域分析成果，选用一定的Cs/Cv值作为初始值。

（2）三点法。所谓三点法，就是根据实测资料系列（连序、不连序系列）计算并点绘经验点，目估过点群中心定出经验频率曲线后，在曲线上按照点子的频率范围选取三个点，并查出各点坐标值（p1，xp1）、（p2，xp2）（p3，xp3），利用水文统计中离均系数Φ＝，则可建立如下联立方程

联解以上方程组，得出下列公式

式中　S——偏度系数，是p和Cs的函数，当p一定，S仅为Cs的函数，S和Cs的关系由附表3查算；

其他符号含义同前。

三点的取法应结合经验点最前一点和最后一点的频率大小分别选1%-50%-99%，3%-50%-97%，5%-50%-95%或10%-50%-90%等。

当然，统计参数初值的估算还有其他方法，如概率权重法、权函数法等，这里不作详细介绍，可参考有关专业书籍。但不管用何种方法初估统计参数，最后都要经过频率适线来确定参数。

2.洪水频率曲线线型与适线原则

《水利水电工程设计洪水计算规范》（SL44—2006）中指出，洪水频率曲线的线型应采用皮尔逊Ⅲ型。对特殊情况，经过论证后也可采用其他线型。

在洪水频率计算中，推求洪水特征值的理论频率曲线，目前我国普遍采用适线法。适线法有两种：一种是经验适线法（或称目估适线法）；另一种是优化适线法。

经验适线法是在经验频率点据和频率曲线线型确定之后，通过调整参数选配一条与经验点据配合最佳的理论频率曲线。适线的原则如下：

（1）适线时尽量照顾点群趋势，使曲线上、下两侧点子数目大致相等，并交错均匀分布。若全部点据配合有困难，可侧重考虑上部和中部点子。

（2）应分析经验点据的精度，使曲线尽量地接近或通过比较可靠的点据。

（3）历史洪水，特别是为首的几个历史特大洪水，一般精度较差，适线时，不宜机械地通过这些点据，而使频率曲线脱离点群；但也不能为照顾点群趋势使曲线离开特大值太远，应考虑特大历史洪水的可能误差范围，以便调整频率曲线。

（4）要考虑不同历时洪水特征值参数的变化规律，以及同一历时的参数在地区上变化规律的合理性。

优化适线法，通常是在计算机上进行，适线的准则可根据各项洪水的误差情况，采用离差平方和准则或相对离差平方和准则。

【例G2.2】某流域拟建中型水库一座。经分析确定水库枢纽本身永久水工建筑物正常运用洪水标准（设计标准）p＝1%，非常运用洪水标准（校核标准）p＝0.1%。该工程坝址位置有31年实测洪水资料（1952～1982年），经选样审查后洪峰流量资料列入表G2.7第②栏，为了提高资料的代表性，曾多次进行洪水调查，得知1788年发生特大洪水，洪峰流量为9200m3/s，经考证是1788年以来最大值；1909年洪峰流量为6710m3/s，是1909年以来的第二位；实测系列中1954年洪峰流量7400m3/s，为1909年以来的第一位。试推求p＝1%、p＝0.1%的设计洪峰流量。

解：（1）计算经验频率。用分别处理法计算各年最大洪峰流量的经验频率，见表G2.7。

（2）用三点法初估洪峰流量系列统计参数的初值。根据表G2.7在频率格纸上点绘经验频率点据，通过点群中心目估绘出一条光滑的经验频率曲线，如图G2.3中的虚线。根据频率范围在该线上读取p＝5%、50%、95%三点的洪峰流量分别为：

Q5%＝5600m3/s；Q50%＝2500m3/s；Q95%＝1230m3/s

由式（G2.8）计算偏度系数S

由S查用表（附表3）得Cs＝1.49。

由Cs查附表4，得到Φ50%＝-0.237，Φ5%-Φ95%＝3.093，代入式（G2.9）、式（G2.10）

得

所以

表G2.7　经验频率曲线计算成果表

（2）三点法。所谓三点法，就是根据实测资料系列（连序、不连序系列）计算并点绘经验点，目估过点群中心定出经验频率曲线后，在曲线上按照点子的频率范围选取三个点，并查出各点坐标值（p1，xp1）、（p2，xp2）（p3，xp3），利用水文统计中离均系数Φ＝，则可建立如下联立方程

联解以上方程组，得出下列公式

式中　S——偏度系数，是p和Cs的函数，当p一定，S仅为Cs的函数，S和Cs的关系由附表3查算；

其他符号含义同前。

三点的取法应结合经验点最前一点和最后一点的频率大小分别选1%-50%-99%，3%-50%-97%，5%-50%-95%或10%-50%-90%等。

当然，统计参数初值的估算还有其他方法，如概率权重法、权函数法等，这里不作详细介绍，可参考有关专业书籍。但不管用何种方法初估统计参数，最后都要经过频率适线来确定参数。

2.洪水频率曲线线型与适线原则

《水利水电工程设计洪水计算规范》（SL44—2006）中指出，洪水频率曲线的线型应采用皮尔逊Ⅲ型。对特殊情况，经过论证后也可采用其他线型。

在洪水频率计算中，推求洪水特征值的理论频率曲线，目前我国普遍采用适线法。适线法有两种：一种是经验适线法（或称目估适线法）；另一种是优化适线法。

经验适线法是在经验频率点据和频率曲线线型确定之后，通过调整参数选配一条与经验点据配合最佳的理论频率曲线。适线的原则如下：

（1）适线时尽量照顾点群趋势，使曲线上、下两侧点子数目大致相等，并交错均匀分布。若全部点据配合有困难，可侧重考虑上部和中部点子。

（2）应分析经验点据的精度，使曲线尽量地接近或通过比较可靠的点据。

（3）历史洪水，特别是为首的几个历史特大洪水，一般精度较差，适线时，不宜机械地通过这些点据，而使频率曲线脱离点群；但也不能为照顾点群趋势使曲线离开特大值太远，应考虑特大历史洪水的可能误差范围，以便调整频率曲线。

（4）要考虑不同历时洪水特征值参数的变化规律，以及同一历时的参数在地区上变化规律的合理性。

优化适线法，通常是在计算机上进行，适线的准则可根据各项洪水的误差情况，采用离差平方和准则或相对离差平方和准则。

【例G2.2】某流域拟建中型水库一座。经分析确定水库枢纽本身永久水工建筑物正常运用洪水标准（设计标准）p＝1%，非常运用洪水标准（校核标准）p＝0.1%。该工程坝址位置有31年实测洪水资料（1952～1982年），经选样审查后洪峰流量资料列入表G2.7第②栏，为了提高资料的代表性，曾多次进行洪水调查，得知1788年发生特大洪水，洪峰流量为9200m3/s，经考证是1788年以来最大值；1909年洪峰流量为6710m3/s，是1909年以来的第二位；实测系列中1954年洪峰流量7400m3/s，为1909年以来的第一位。试推求p＝1%、p＝0.1%的设计洪峰流量。

解：（1）计算经验频率。用分别处理法计算各年最大洪峰流量的经验频率，见表G2.7。

（2）用三点法初估洪峰流量系列统计参数的初值。根据表G2.7在频率格纸上点绘经验频率点据，通过点群中心目估绘出一条光滑的经验频率曲线，如图G2.3中的虚线。根据频率范围在该线上读取p＝5%、50%、95%三点的洪峰流量分别为：

Q5%＝5600m3/s；Q50%＝2500m3/s；Q95%＝1230m3/s

由式（G2.8）计算偏度系数S

由S查用表（附表3）得Cs＝1.49。

由Cs查附表4，得到Φ50%＝-0.237，Φ5%-Φ95%＝3.093，代入式（G2.9）、式（G2.10）

得

所以

表G2.7　经验频率曲线计算成果表

（3）适线并推求设计值。现按＝2835m3/s，Cv＝0.50，选取Cs＝3.0Cv进行适线，曲线与点子配合欠佳，需要调整参数；故又令＝2840m3/s，Cv＝0.50，选取Cs＝3.5Cv，再次适线，配合较好，如图G2.3中的实线，故最后采用该参数作为设计依据。

根据采用的参数推求坝址断面处千年一遇的设计洪峰流量Qm＝10735m3/s。

G2.2.2.5　频率计算成果的合理性检查

为了避免单一洪水特征值系列频率计算的任意性以及减小频率计算的抽样误差，应对频率计算成果（指适线后得到的统计参数或设计值）根据本站洪峰、不同时段洪量统计参数和设计值的变化规律，以及上下游、干支流和邻近流域各站的成果进行合理性检查。检查时，一方面要分析一般规律，检查成果是否合理，必要时可作适当调整；另一方面，也要注意是否具有特殊性，发现问题，找出原因。

合理性检查常用的方法可以归纳为以下几个方面：

图G2.3　某站洪峰流量频率曲线图

1—经验频率曲线；2—理论频率曲线

（1）本站洪峰流量及不同时段洪量频率计算成果比较。

1）一般情况下，各种时段的洪量均值和设计值，随时段的增长而加大；变差系数Cv值随时段的增长而减小。但对于调蓄作用大且连续暴雨次数多的河流，各时段洪量Cv值随时段增长反而增大，至某时段达到最大值后再逐渐减小。

2）各种时段洪量频率曲线绘于同一张频率格纸上，各条曲线在使用范围内不得相互交叉。

（2）与上下游及邻近站的频率计算成果比较。

1）同一条河流的上下游站，当气候及地形等条件相似时，洪峰流量、洪量的均值及设计值由上游向下游呈递增的变化规律，其模数则递减。而变差系数Cv值往往由上游向下游呈递减趋势。当上下游站气候及下垫面条件不一致时，各项参数及设计值的变化规律比较复杂，需要结合自然地理及暴雨分布特性等因素进一步分析论证，判断是否符合应有的规律。

2）与邻近河流的计算成果比较，通常用洪峰流量模数的变化规律加以分析，一般情况下，洪峰流量的模数随流域面积的增大而减小。

（3）与暴雨频率分析计算成果比较。暴雨与洪水有着密切的因果关系。因此，不同时段暴雨量的统计参数与相应时段洪量的统计参数应有一定的关系。

洪水径流深（均值或设计值）应小于相应时段的暴雨深（均值或设计值）；一般情况下，洪量的变差系数Cv应大于相应时段暴雨的Cv。

由于洪水特征值影响因素的复杂性，上述分析方法所依据的规律并不十分严密，所以分析时必须作多方面论证，不可生搬硬套。如发现不合理现象，应认真查明原因，并应重新审查原始资料的可靠性、一致性和代表性以及复核整个计算过程。

G2.2.2.6　设计洪峰及洪量的确定与安全修正值

由适线法求得洪峰、洪量的理论频率曲线后，根据指定频率，则可确定设计洪峰和不同时段的设计洪量。

在洪水频率计算中，虽然考虑了特大洪水延长了系列，在一定程度上提高了代表性，但洪水资料系列仍然是无限总体中的一个样本，由此样本求得统计参数和设计值，必然存在抽样误差。对于大型水利水电工程或重点中型工程，如果经过综合分析发现设计值确有可能偏小时，为了安全起见，可在校核洪水的基础上加一安全修正值。

安全修正值的大小，可根据综合分析成果偏小的可能幅度来计算，但规范规定安全修正值一般以不超过计算值的20%为宜。

（3）适线并推求设计值。现按＝2835m3/s，Cv＝0.50，选取Cs＝3.0Cv进行适线，曲线与点子配合欠佳，需要调整参数；故又令＝2840m3/s，Cv＝0.50，选取Cs＝3.5Cv，再次适线，配合较好，如图G2.3中的实线，故最后采用该参数作为设计依据。

根据采用的参数推求坝址断面处千年一遇的设计洪峰流量Qm＝10735m3/s。

G2.2.2.5　频率计算成果的合理性检查

为了避免单一洪水特征值系列频率计算的任意性以及减小频率计算的抽样误差，应对频率计算成果（指适线后得到的统计参数或设计值）根据本站洪峰、不同时段洪量统计参数和设计值的变化规律，以及上下游、干支流和邻近流域各站的成果进行合理性检查。检查时，一方面要分析一般规律，检查成果是否合理，必要时可作适当调整；另一方面，也要注意是否具有特殊性，发现问题，找出原因。

合理性检查常用的方法可以归纳为以下几个方面：

图G2.3　某站洪峰流量频率曲线图

1—经验频率曲线；2—理论频率曲线

（1）本站洪峰流量及不同时段洪量频率计算成果比较。

1）一般情况下，各种时段的洪量均值和设计值，随时段的增长而加大；变差系数Cv值随时段的增长而减小。但对于调蓄作用大且连续暴雨次数多的河流，各时段洪量Cv值随时段增长反而增大，至某时段达到最大值后再逐渐减小。

2）各种时段洪量频率曲线绘于同一张频率格纸上，各条曲线在使用范围内不得相互交叉。

（2）与上下游及邻近站的频率计算成果比较。

1）同一条河流的上下游站，当气候及地形等条件相似时，洪峰流量、洪量的均值及设计值由上游向下游呈递增的变化规律，其模数则递减。而变差系数Cv值往往由上游向下游呈递减趋势。当上下游站气候及下垫面条件不一致时，各项参数及设计值的变化规律比较复杂，需要结合自然地理及暴雨分布特性等因素进一步分析论证，判断是否符合应有的规律。

2）与邻近河流的计算成果比较，通常用洪峰流量模数的变化规律加以分析，一般情况下，洪峰流量的模数随流域面积的增大而减小。

（3）与暴雨频率分析计算成果比较。暴雨与洪水有着密切的因果关系。因此，不同时段暴雨量的统计参数与相应时段洪量的统计参数应有一定的关系。

洪水径流深（均值或设计值）应小于相应时段的暴雨深（均值或设计值）；一般情况下，洪量的变差系数Cv应大于相应时段暴雨的Cv。

由于洪水特征值影响因素的复杂性，上述分析方法所依据的规律并不十分严密，所以分析时必须作多方面论证，不可生搬硬套。如发现不合理现象，应认真查明原因，并应重新审查原始资料的可靠性、一致性和代表性以及复核整个计算过程。

G2.2.2.6　设计洪峰及洪量的确定与安全修正值

由适线法求得洪峰、洪量的理论频率曲线后，根据指定频率，则可确定设计洪峰和不同时段的设计洪量。

在洪水频率计算中，虽然考虑了特大洪水延长了系列，在一定程度上提高了代表性，但洪水资料系列仍然是无限总体中的一个样本，由此样本求得统计参数和设计值，必然存在抽样误差。对于大型水利水电工程或重点中型工程，如果经过综合分析发现设计值确有可能偏小时，为了安全起见，可在校核洪水的基础上加一安全修正值。

安全修正值的大小，可根据综合分析成果偏小的可能幅度来计算，但规范规定安全修正值一般以不超过计算值的20%为宜。