AutoCAD绘图提示:按工程制图国家标准绘制图形。学校绘图学习期间可根据图形实际情况建议进行如下设置。a. 将所绘图形按比例匹配在A3图幅,视图缩放,保存为“学号+姓名”并提交。扫一扫,看图形细节图4-3道砟桥面T形桥台总图___________任务报告训练4:按工程制图要求抄绘图4-4T形桥台台顶构造图 并进行打印输出。扫一扫,看图形细节图4-14建筑施工图___________任务报告训练15:按标注抄绘图4-15建筑施工图。......
2025-09-29
设由变量x,y的同期样本系列构成n组观测值(xi,yi),i=1~n,并设待求变量为y,称为倚变量,主要影响因素x为自变量。以倚变量y为纵坐标,自变量x为横坐标,点绘散点图,如图X3.16(a)所示,点群呈现密集的带状分布,且为直线趋势,则可用相关图解法或相关计算法进行简单直线相关分析,选配直线方程
1.相关图解法
根据散点图,通过点群中心,目估定出相关直线,如图X3.16(a)的直线所示。由直线上的两点可确定式(X3.29)中a、b两个参数;也可由图上直接求得,即a为直线在纵轴上的截距,b为直线的斜率。
用目估定线时应注意以下几点:应使相关线两侧点据的正离差之和与负离差之和大致相等;对离差较大的个别点不得轻率的删略,须查明原因,如果没有错误或不合理之处,定线时还要适当照顾,但不易过分迁就,要全盘考虑相关点的总趋势;相关线应通过同步系列的均值点![]() ,这可由下述的相关计算法得到证明。
,这可由下述的相关计算法得到证明。
相关直线方程反映了相关变量之间的近似关系。根据相关直线或相关方程就可由x插补延长系列y。
相关图解法简便实用,一般精度尚可,但目估定线有一定的任意性,且不能定量描述相关的密切程度和估计误差。
2.相关计算法
(1)确定相关方程的准则。根据散点图可确定很多条直线,由于建立相关方程式(X3.29)的目的是由x求y,很自然的一个想法是希望观测点在倚变量y方向上最靠近所求的相关直线。由图X3.17可见,观测点(xi,yi)与相关直线在纵坐标方向上的离差Δyi为
图X3.17 相关分析示意图
式中 yi——观测点的纵坐标,i=1,2,…,n;
用目估定线时应注意以下几点:应使相关线两侧点据的正离差之和与负离差之和大致相等;对离差较大的个别点不得轻率的删略,须查明原因,如果没有错误或不合理之处,定线时还要适当照顾,但不易过分迁就,要全盘考虑相关点的总趋势;相关线应通过同步系列的均值点![]() ,这可由下述的相关计算法得到证明。
,这可由下述的相关计算法得到证明。
相关直线方程反映了相关变量之间的近似关系。根据相关直线或相关方程就可由x插补延长系列y。
相关图解法简便实用,一般精度尚可,但目估定线有一定的任意性,且不能定量描述相关的密切程度和估计误差。
2.相关计算法
(1)确定相关方程的准则。根据散点图可确定很多条直线,由于建立相关方程式(X3.29)的目的是由x求y,很自然的一个想法是希望观测点在倚变量y方向上最靠近所求的相关直线。由图X3.17可见,观测点(xi,yi)与相关直线在纵坐标方向上的离差Δyi为
图X3.17 相关分析示意图
式中 yi——观测点的纵坐标,i=1,2,…,n;
![]() ——由xi根据相关直线求得的纵坐标值,i=1,2,…,n。
——由xi根据相关直线求得的纵坐标值,i=1,2,…,n。
我们希望整体拟合“最佳”,即
为最小。按照这一准则确定的相关直线称最小二乘法准则,由此求得的相关方程称为y倚x的回归方程,相应相关直线也称为回归线。
(2)回归方程的确定。确定回归方程,即推求参数a、b。欲使式(X3.30)取得最小值,可分别对a及b求一阶偏导数并使其等于零。即令
联解方程组得
其中
![]() ——由xi根据相关直线求得的纵坐标值,i=1,2,…,n。
——由xi根据相关直线求得的纵坐标值,i=1,2,…,n。
我们希望整体拟合“最佳”,即
为最小。按照这一准则确定的相关直线称最小二乘法准则,由此求得的相关方程称为y倚x的回归方程,相应相关直线也称为回归线。
(2)回归方程的确定。确定回归方程,即推求参数a、b。欲使式(X3.30)取得最小值,可分别对a及b求一阶偏导数并使其等于零。即令
联解方程组得
其中
式中 ![]() ——x、y系列的均值;
——x、y系列的均值;
sx、sy——x、y系列的均方差;
式中 ![]() ——x、y系列的均值;
——x、y系列的均值;
sx、sy——x、y系列的均方差;
![]() ——x、y系列的模比系数;
——x、y系列的模比系数;
r——相关系数,表示x、y之间线性相关的密切程度。
将式(X3.31)、式(X3.32)代入式(X3.29)得y倚x的回归方程
![]() ——x、y系列的模比系数;
——x、y系列的模比系数;
r——相关系数,表示x、y之间线性相关的密切程度。
将式(X3.31)、式(X3.32)代入式(X3.29)得y倚x的回归方程
![]() 为回归线的斜率,称y倚x的回归系数,并记为Ry/x,即
为回归线的斜率,称y倚x的回归系数,并记为Ry/x,即
上述是y倚x的回归方程,即x为自变量,y为倚变量,应用于由x求y。若由y求x,则要建立x倚y的回归方程。同理,可推得x倚y的回归方程
![]() 为回归线的斜率,称y倚x的回归系数,并记为Ry/x,即
为回归线的斜率,称y倚x的回归系数,并记为Ry/x,即
上述是y倚x的回归方程,即x为自变量,y为倚变量,应用于由x求y。若由y求x,则要建立x倚y的回归方程。同理,可推得x倚y的回归方程
必须指出,对于相关关系,y倚x与x倚y的两条回归线是不重合的,但有一公共交点![]() 。使用时,必须根据问题的需要正确确定倚变量和自变量系列。
。使用时,必须根据问题的需要正确确定倚变量和自变量系列。
(3)回归线的误差。由回归方程所确定的回归线是在最小二乘法准则情况下与观测点的最佳配合线,观测点不会完全落在此线上,而是分布于两侧。因此,回归方程只反映两变量之间的平均关系,由x利用回归方程求y不可避免存在误差。数理统计中经过研究,由式(X3.37)估计回归方程的误差
称δy为y倚x回归线的均方误,式中各符号含义同前。
必须指出,对于相关关系,y倚x与x倚y的两条回归线是不重合的,但有一公共交点![]() 。使用时,必须根据问题的需要正确确定倚变量和自变量系列。
。使用时,必须根据问题的需要正确确定倚变量和自变量系列。
(3)回归线的误差。由回归方程所确定的回归线是在最小二乘法准则情况下与观测点的最佳配合线,观测点不会完全落在此线上,而是分布于两侧。因此,回归方程只反映两变量之间的平均关系,由x利用回归方程求y不可避免存在误差。数理统计中经过研究,由式(X3.37)估计回归方程的误差
称δy为y倚x回归线的均方误,式中各符号含义同前。
回归线的均方误δy与y系列的均方差δy从性质上是不同的。前者是由观测点(xi,yi)与相关直线在纵坐标方向上的离差求得,是回归线与所有观测点的平均误差,从平均意义上反映了相关直线与观测点配合的密切程度;后者是由y系列的各观测值yi与系列的均值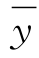 之间的离差求得,反映的是y系列的离散程度。根据统计学原理,可以证明
之间的离差求得,反映的是y系列的离散程度。根据统计学原理,可以证明
如前所述,由于回归方程反映x与y的近似关系,因此,对于任意给定的x0,由回归方程求得y0=a+bx0,仅仅是许多可能值y0i的平均数。按照误差原理,这些可能值y0i落在回归线两侧一个均方误δy范围内的概率为68.3%,落在回归线两侧3个均方误δy范围内的概率为99.7%,如图X3.18所示。
图X3.18 y倚x的回归线的误差范围
同理,对于x倚y的回归方程,回归线的均方误为
必须指出,在讨论上述误差时,没有考虑样本的抽样误差。事实上,只要用样本资料来估计回归方程中的参数,抽样误差就必然存在。可以证明,这种抽样误差在回归线的中段误差较小,而在上下段较大,在使用回归线时,应给予注意。
(4)相关系数。由式(X3.38)或式(X3.40)容易得出,r2≤1。并且:
1)若r2=1,则均方误δy=0,表明关系点(xi,yi),i=1,2,…,n,均落在回归线上,两变量为线性函数关系。
2)若r2=0,则均方误δy=sy,此时误差达最大值,说明变量之间无线性关系。
3)若r2<1,即0<|r|<1,则变量之间存在线性相关关系。r>0,称为正相关;r<0,称为负相关。|r|越大,两变量线性相关越密切。
回归线的均方误δy与y系列的均方差δy从性质上是不同的。前者是由观测点(xi,yi)与相关直线在纵坐标方向上的离差求得,是回归线与所有观测点的平均误差,从平均意义上反映了相关直线与观测点配合的密切程度;后者是由y系列的各观测值yi与系列的均值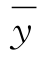 之间的离差求得,反映的是y系列的离散程度。根据统计学原理,可以证明
之间的离差求得,反映的是y系列的离散程度。根据统计学原理,可以证明
如前所述,由于回归方程反映x与y的近似关系,因此,对于任意给定的x0,由回归方程求得y0=a+bx0,仅仅是许多可能值y0i的平均数。按照误差原理,这些可能值y0i落在回归线两侧一个均方误δy范围内的概率为68.3%,落在回归线两侧3个均方误δy范围内的概率为99.7%,如图X3.18所示。
图X3.18 y倚x的回归线的误差范围
同理,对于x倚y的回归方程,回归线的均方误为
必须指出,在讨论上述误差时,没有考虑样本的抽样误差。事实上,只要用样本资料来估计回归方程中的参数,抽样误差就必然存在。可以证明,这种抽样误差在回归线的中段误差较小,而在上下段较大,在使用回归线时,应给予注意。
(4)相关系数。由式(X3.38)或式(X3.40)容易得出,r2≤1。并且:
1)若r2=1,则均方误δy=0,表明关系点(xi,yi),i=1,2,…,n,均落在回归线上,两变量为线性函数关系。
2)若r2=0,则均方误δy=sy,此时误差达最大值,说明变量之间无线性关系。
3)若r2<1,即0<|r|<1,则变量之间存在线性相关关系。r>0,称为正相关;r<0,称为负相关。|r|越大,两变量线性相关越密切。
那么,|r|多大时,可以认为两变量线性相关显著?水文计算中一般要求n在10或12以上,且|r|≥0.8时,成果方可应用。有关其数理统计的理论依据可参考文献[5]。研究表明,相关系数一定时,倚变量的变差系数越大,回归方程的均方误就越大。因此,仅用相关系数作为判别密切与否的标准不够全面,实际应用时,通常要求回归线的均方误δy应小于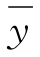 的15%。(https://www.chuimin.cn)
的15%。(https://www.chuimin.cn)
进一步指出,相关系数表示x、y之间线性相关的密切程度。若r=0,只表示两变量之间无线性关系,但可能存在曲线关系,需要根据散点图的趋势进行分析,当曲线关系较密切时,则进行曲线相关。
3.相关分析中应注意的问题
相关分析中除了上述对样本容量、相关系数、回归线的均方误等方面的要求外,还应注意以下几点:
(1)使用相关分析方法,首先应分析论证变量之间在物理成因上确实存在着联系。要防止假相关。所谓假相关是指本来不相关或弱相关的两个变量,由于通过数学上的某种处理(例如两者都加入第三个变量),而使相关关系变得十分密切。为避免假相关,应直接研究变量之间的关系。
(2)在插补延长资料时,如果超出实测点控制的部分,应特别慎重。外延部分一般不宜超过实际幅度的50%。
(3)避免辗转相关。例如,有x、y、z三个变量的实测系列,x系列较长,而y、z系列较短。其中z是待求变量,由x插补z时,z与x的相关系数较小。而y与x、y与z相关系数均较大。欲由x插补z,就先通过y与x相关插补y,再进行z与y相关插补z,这就是辗转相关。研究表明,辗转相关的误差,一定不会小于直接相关的误差,辗转相关是不可取的。
【例X3.5】 湿润地区某流域具有1966~2025年的年径流深和1958~1978的年降水量资料,见表X3.5。试用相关计算法进行相关分析,并插补流域的年径流深资料。
同一流域年径流深与年降水量成因上有联系,因此可进行相关计算。本例相关分析的目的是由年降水量插补延长年径流深系列,故年降水量为自变量x,年径流深为倚变量y。绘散点图如图X3.19所示,由图可见,点群分布趋势呈直线,故可作y倚x的直线回归计算。
表X3.5 某流域年降水量与年径流深资料 单位:mm
利用Excel完成直线回归计算是非常方便的,可采用两种途径进行计算。
第一种途径是利用Excel的计算功能,分步完成[例X3.5]相关计算的各项内容。计算操作步骤如下:
图X3.19 某流域年径流深与年降水量相关图
(1)新建一个Excel工作表,用常规数据格式在A列输入相关计算同步资料相应的年份,B列输入自变量年降水量x值,C列输入倚变量年径流深y值,并在单元格D2~J2中建立相关计算有关项目的表头,如图X3.20所示。
图X3.20 相关分析计算
(2)分别利用前述介绍的平均值函数“AVERAGE”计算年降水量x值和年径流深y的均值,其结果如图X3.20的单元格B17、C17中的数据所示。
那么,|r|多大时,可以认为两变量线性相关显著?水文计算中一般要求n在10或12以上,且|r|≥0.8时,成果方可应用。有关其数理统计的理论依据可参考文献[5]。研究表明,相关系数一定时,倚变量的变差系数越大,回归方程的均方误就越大。因此,仅用相关系数作为判别密切与否的标准不够全面,实际应用时,通常要求回归线的均方误δy应小于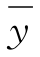 的15%。
的15%。
进一步指出,相关系数表示x、y之间线性相关的密切程度。若r=0,只表示两变量之间无线性关系,但可能存在曲线关系,需要根据散点图的趋势进行分析,当曲线关系较密切时,则进行曲线相关。
3.相关分析中应注意的问题
相关分析中除了上述对样本容量、相关系数、回归线的均方误等方面的要求外,还应注意以下几点:
(1)使用相关分析方法,首先应分析论证变量之间在物理成因上确实存在着联系。要防止假相关。所谓假相关是指本来不相关或弱相关的两个变量,由于通过数学上的某种处理(例如两者都加入第三个变量),而使相关关系变得十分密切。为避免假相关,应直接研究变量之间的关系。
(2)在插补延长资料时,如果超出实测点控制的部分,应特别慎重。外延部分一般不宜超过实际幅度的50%。
(3)避免辗转相关。例如,有x、y、z三个变量的实测系列,x系列较长,而y、z系列较短。其中z是待求变量,由x插补z时,z与x的相关系数较小。而y与x、y与z相关系数均较大。欲由x插补z,就先通过y与x相关插补y,再进行z与y相关插补z,这就是辗转相关。研究表明,辗转相关的误差,一定不会小于直接相关的误差,辗转相关是不可取的。
【例X3.5】 湿润地区某流域具有1966~2025年的年径流深和1958~1978的年降水量资料,见表X3.5。试用相关计算法进行相关分析,并插补流域的年径流深资料。
同一流域年径流深与年降水量成因上有联系,因此可进行相关计算。本例相关分析的目的是由年降水量插补延长年径流深系列,故年降水量为自变量x,年径流深为倚变量y。绘散点图如图X3.19所示,由图可见,点群分布趋势呈直线,故可作y倚x的直线回归计算。
表X3.5 某流域年降水量与年径流深资料 单位:mm
利用Excel完成直线回归计算是非常方便的,可采用两种途径进行计算。
第一种途径是利用Excel的计算功能,分步完成[例X3.5]相关计算的各项内容。计算操作步骤如下:
图X3.19 某流域年径流深与年降水量相关图
(1)新建一个Excel工作表,用常规数据格式在A列输入相关计算同步资料相应的年份,B列输入自变量年降水量x值,C列输入倚变量年径流深y值,并在单元格D2~J2中建立相关计算有关项目的表头,如图X3.20所示。
图X3.20 相关分析计算
(2)分别利用前述介绍的平均值函数“AVERAGE”计算年降水量x值和年径流深y的均值,其结果如图X3.20的单元格B17、C17中的数据所示。
(3)利用“数学与三角函数”中的“ROUND”函数分别计算D~J列数据,并按指定的位数对数值进行四舍五入。例如,计算D列数据![]() ,并保留三位小数,具体方法是,在D3单元格输入“=ROUND(B3/1499.9,3)”,然后按“Enter”键,即在D3单元格得到数据“0.976”;接着,选中D3单元格,鼠标指针变成黑十字时,按住鼠标左键,向下拖动填充D4~D15单元格,即得到D列数据
,并保留三位小数,具体方法是,在D3单元格输入“=ROUND(B3/1499.9,3)”,然后按“Enter”键,即在D3单元格得到数据“0.976”;接着,选中D3单元格,鼠标指针变成黑十字时,按住鼠标左键,向下拖动填充D4~D15单元格,即得到D列数据![]() ;进一步利用工具栏“Σ”求和,即得到该列合计值“13.001”。上述各个环节的结果,如图X3.20中的D列数据所示。
;进一步利用工具栏“Σ”求和,即得到该列合计值“13.001”。上述各个环节的结果,如图X3.20中的D列数据所示。
(3)利用“数学与三角函数”中的“ROUND”函数分别计算D~J列数据,并按指定的位数对数值进行四舍五入。例如,计算D列数据![]() ,并保留三位小数,具体方法是,在D3单元格输入“=ROUND(B3/1499.9,3)”,然后按“Enter”键,即在D3单元格得到数据“0.976”;接着,选中D3单元格,鼠标指针变成黑十字时,按住鼠标左键,向下拖动填充D4~D15单元格,即得到D列数据
,并保留三位小数,具体方法是,在D3单元格输入“=ROUND(B3/1499.9,3)”,然后按“Enter”键,即在D3单元格得到数据“0.976”;接着,选中D3单元格,鼠标指针变成黑十字时,按住鼠标左键,向下拖动填充D4~D15单元格,即得到D列数据![]() ;进一步利用工具栏“Σ”求和,即得到该列合计值“13.001”。上述各个环节的结果,如图X3.20中的D列数据所示。
;进一步利用工具栏“Σ”求和,即得到该列合计值“13.001”。上述各个环节的结果,如图X3.20中的D列数据所示。
采用与上述类似的方法,指定欲计算数据要保留的小数位数,可分别计算![]()
![]() ,计算结果如图X3.20中的E~J列数据所示。
,计算结果如图X3.20中的E~J列数据所示。
(4)依据式(X3.15)、式(X3.33)、式(X3.35)、式(X3.32)、式(X3.38),分别计算均方差、相关系数、回归系数、纵轴截距、回归线的均方误。为便于读者结合公式领会计算方法,图X3.20中给出了各个量的计算公式。例如,计算年降水量x系列的均方差的方法是,在单元格E20中输入“=B17SQRT(H16/(13-1))”,然后按“Enter”键,则在E20单元格得到数据“135.7”。与之类似,可计算其他各个量,并得到回归方程,结果如图X3.20所示。当然,样本均方差的计算,也可采用前面介绍的函数“STDEV”计算。
采用与上述类似的方法,指定欲计算数据要保留的小数位数,可分别计算![]()
![]() ,计算结果如图X3.20中的E~J列数据所示。
,计算结果如图X3.20中的E~J列数据所示。
(4)依据式(X3.15)、式(X3.33)、式(X3.35)、式(X3.32)、式(X3.38),分别计算均方差、相关系数、回归系数、纵轴截距、回归线的均方误。为便于读者结合公式领会计算方法,图X3.20中给出了各个量的计算公式。例如,计算年降水量x系列的均方差的方法是,在单元格E20中输入“=B17SQRT(H16/(13-1))”,然后按“Enter”键,则在E20单元格得到数据“135.7”。与之类似,可计算其他各个量,并得到回归方程,结果如图X3.20所示。当然,样本均方差的计算,也可采用前面介绍的函数“STDEV”计算。
(5)由年降水量插补年径流深。由上述计算结果可见,本例n>12,r>0.8,且![]() =8.7%<15%,故相关成果可用于插补年径流深。具体方法是,输入需插补年径流深的年份及相应的年降水量,如图X3.21(a)所示,然后在C3单元格输入“=1.004B3-810.5”,再按下“Enter”键,即得到插补的2025年的年径流深540.6mm。接着选中C3单元格,鼠标指针变成黑十字时,按住鼠标左键,向下拖动填充C4~C10单元格,即得到1959~2025年插补的年径流深,如图X3.21(b)所示。
=8.7%<15%,故相关成果可用于插补年径流深。具体方法是,输入需插补年径流深的年份及相应的年降水量,如图X3.21(a)所示,然后在C3单元格输入“=1.004B3-810.5”,再按下“Enter”键,即得到插补的2025年的年径流深540.6mm。接着选中C3单元格,鼠标指针变成黑十字时,按住鼠标左键,向下拖动填充C4~C10单元格,即得到1959~2025年插补的年径流深,如图X3.21(b)所示。
图X3.21 由年降水量插补年径流深
(a)输入回归方程;(b)拖动填充
第二种途径是直接利用Excel软件的图表向导功能直接绘出相关直线,并求出相关直线方程及相关系数,其步骤如下:
(1)打开Excel新建一个工作簿,用常规数据格式在A列输入相关计算同步资料相应的年份,B列输入自变量年降水量x值,C列输入倚变量年径流深y值。
(2)点击菜单栏“插入”→“图表”,出现“图表向导—4步骤之1—图表类型”对话框后,选择XY散点图,单击“下一步”按钮。
(3)出现“图表向导—4步骤之2—图表源数据”对话框后,选择“数据区域=Sheet1!$B$3:$C$15,系列X=Sheet1!$B$3:$B$15,系列Y=Sheet1!$C$3:$C$15”;或者用鼠标拖动选择图X3.22中的阴影数据区域;然后在“系列产生在”区选择“列”,再单击“下一步”按钮。
图X3.22 利用Excel“图表向导”建立散点图
(4)出现“图表向导—4步骤之3—图表选项”对话框后,选择“标题”标签,在“图表标题”栏中输入“某站年降雨量与年径流深相关图”、在“数值X轴(A)”栏输入“年降雨量X(mm)”、“数值Y轴(V)”栏输入“年径流深Y(mm)”;选择“坐标轴”标签,在“主坐标轴数值X轴(A)、数值Y轴(V)”前打“√”;选择“网格线”标签,在“数值X轴主要网格线、数值Y轴主要网格线”前打“√”;然后单击“下一步”按钮。
(5)出现“图表向导—4步骤之4—图表位置”对话框后,选择“作为其中的对象插入”,然后单击“完成”按钮,即得到如图X3.22所示的散点图。
(6)将光标放在绘图区内任一相关点上并单击鼠标右键,选“添加趋势线”,在“类型”标签中,选“线性”;在“选项”标签中的“显示公式”、“显示R平方值”前面打“√”,然后单击“确定”,即得到相关线及有关计算结果,如图X3.23所示。对于线性相关分析,“R平方值”即为线性相关系数的平方值。
进一步可对绘图区、坐标轴等处单击鼠标右键,选择有关项目,进而分别对绘图区、坐标轴等处的格式进行设置与修改,读者可上机练习,在此不详细介绍。
根据需要,可将上述各计算表或图形复制到Word文档中。
图X3.23 添加趋势线并得到相关方程
以上两种途径的计算结果完全一致。显然,采用Excel的图表功能计算与绘图,使得简单直线相关变得更为简便易行。
(5)由年降水量插补年径流深。由上述计算结果可见,本例n>12,r>0.8,且![]() =8.7%<15%,故相关成果可用于插补年径流深。具体方法是,输入需插补年径流深的年份及相应的年降水量,如图X3.21(a)所示,然后在C3单元格输入“=1.004B3-810.5”,再按下“Enter”键,即得到插补的2025年的年径流深540.6mm。接着选中C3单元格,鼠标指针变成黑十字时,按住鼠标左键,向下拖动填充C4~C10单元格,即得到1959~2025年插补的年径流深,如图X3.21(b)所示。
=8.7%<15%,故相关成果可用于插补年径流深。具体方法是,输入需插补年径流深的年份及相应的年降水量,如图X3.21(a)所示,然后在C3单元格输入“=1.004B3-810.5”,再按下“Enter”键,即得到插补的2025年的年径流深540.6mm。接着选中C3单元格,鼠标指针变成黑十字时,按住鼠标左键,向下拖动填充C4~C10单元格,即得到1959~2025年插补的年径流深,如图X3.21(b)所示。
图X3.21 由年降水量插补年径流深
(a)输入回归方程;(b)拖动填充
第二种途径是直接利用Excel软件的图表向导功能直接绘出相关直线,并求出相关直线方程及相关系数,其步骤如下:
(1)打开Excel新建一个工作簿,用常规数据格式在A列输入相关计算同步资料相应的年份,B列输入自变量年降水量x值,C列输入倚变量年径流深y值。
(2)点击菜单栏“插入”→“图表”,出现“图表向导—4步骤之1—图表类型”对话框后,选择XY散点图,单击“下一步”按钮。
(3)出现“图表向导—4步骤之2—图表源数据”对话框后,选择“数据区域=Sheet1!$B$3:$C$15,系列X=Sheet1!$B$3:$B$15,系列Y=Sheet1!$C$3:$C$15”;或者用鼠标拖动选择图X3.22中的阴影数据区域;然后在“系列产生在”区选择“列”,再单击“下一步”按钮。
图X3.22 利用Excel“图表向导”建立散点图
(4)出现“图表向导—4步骤之3—图表选项”对话框后,选择“标题”标签,在“图表标题”栏中输入“某站年降雨量与年径流深相关图”、在“数值X轴(A)”栏输入“年降雨量X(mm)”、“数值Y轴(V)”栏输入“年径流深Y(mm)”;选择“坐标轴”标签,在“主坐标轴数值X轴(A)、数值Y轴(V)”前打“√”;选择“网格线”标签,在“数值X轴主要网格线、数值Y轴主要网格线”前打“√”;然后单击“下一步”按钮。
(5)出现“图表向导—4步骤之4—图表位置”对话框后,选择“作为其中的对象插入”,然后单击“完成”按钮,即得到如图X3.22所示的散点图。
(6)将光标放在绘图区内任一相关点上并单击鼠标右键,选“添加趋势线”,在“类型”标签中,选“线性”;在“选项”标签中的“显示公式”、“显示R平方值”前面打“√”,然后单击“确定”,即得到相关线及有关计算结果,如图X3.23所示。对于线性相关分析,“R平方值”即为线性相关系数的平方值。
进一步可对绘图区、坐标轴等处单击鼠标右键,选择有关项目,进而分别对绘图区、坐标轴等处的格式进行设置与修改,读者可上机练习,在此不详细介绍。
根据需要,可将上述各计算表或图形复制到Word文档中。
图X3.23 添加趋势线并得到相关方程
以上两种途径的计算结果完全一致。显然,采用Excel的图表功能计算与绘图,使得简单直线相关变得更为简便易行。
相关文章

AutoCAD绘图提示:按工程制图国家标准绘制图形。学校绘图学习期间可根据图形实际情况建议进行如下设置。a. 将所绘图形按比例匹配在A3图幅,视图缩放,保存为“学号+姓名”并提交。扫一扫,看图形细节图4-3道砟桥面T形桥台总图___________任务报告训练4:按工程制图要求抄绘图4-4T形桥台台顶构造图 并进行打印输出。扫一扫,看图形细节图4-14建筑施工图___________任务报告训练15:按标注抄绘图4-15建筑施工图。......
2025-09-29

截面法确定扭矩1.扭矩图当轴上同时作用两个以上的外力偶矩时,为了形象地表示各截面扭矩的大小和正负,以便分析危险截面,常需画出扭矩随截面位置变化的图形,这种图形称为扭矩图。作扭矩图:根据上述计算结果,按比例画扭矩图[图6-10]。图6-11扭矩图的简洁画法☆想一想 练一练若两轴上的外力偶矩及各段轴长相等,而截面尺寸不同,其扭矩图相同吗?......
2025-09-29

本实例绘制的物件外壳类符号有S00059、S00060、S00061、S00063,绘制过程如下。命令:_rectang指定第一个角点或[倒角/标高/圆角/厚度/宽度]:30,0↙指定另一个角点或[面积/尺寸/旋转]:@10,10↙绘制的S00059图形符号如图6-1所示。在功能区“默认”选项卡的“绘图”面板中单击“多段线”按钮,接着根据命令行提示进行以下操作。......
2025-09-29

3)单击→,系统将弹出对话框,选择上步创建的基准平面作为草绘平面,并单击选项进入草绘界面。4)选择中的按钮,使草绘平面与屏幕平行,在中心处绘制直径为400.00的圆,如图6-118所示,单击按钮完成草绘。图6-118 绘制圆图6-119 更改拉伸方式图6-120 创建固定板图6-121 模型树......
2025-09-29

学习绘制参考制图有两个意义:一是知道了参考制图的来历,通过绘制参考制图可以达到“印证”平面结构制图的原理。二是有了绘制参考制图的能力,可以将自己创意的优秀样板发表出来,提供给更多人参考制作出漂亮的服装。制作参考制图的步骤如下:1.接合样板把衣身裁片样板接合在一起,注意:前过肩片与前中片不留间隙对合,前中心呈一条直线。绘制参考制图能够“印证”以前学过的结构制图。......
2025-09-29

命令:_circle //单击“圆心、半径”按钮根据需要继续指定其他点来创建构//输入圆心的坐标2.圆心、直径通过指定圆心和直径绘制圆的步骤如下。图2-3 创建构造线的提示选项●“水平”/“垂直”:创建一条经过指定点并且与当前UCS的X或Y轴平行的构造线。......
2025-09-29

使用原型绘制参考制图时,通常要依据服装的款式特点将原型的省量转移到相应的位置上之后再附着原型。绘制本款衬衫的参考制图,需要将原型的省量事先转移到前领围线位置上,然后按照如下顺序绘制参考制图。......
2025-09-29

图4.28运动装置的选择具有主要功能性组件的动力装置通常为简单的调节控制元件,如气缸或简单的旋转装置。主要功能可变的运动装置可进一步分为手动控制和程序控制的动力装置。它们用于在对人类有直接风险的情况下执行人类运动,或用于增强人类能力。图4.29显示了空间中的运动由不同的动力学阶段组成,这些阶段可能会影响机械手,如前所述。图4.29用不同颜色标记的加减速运动轨迹在传感器对运动序列的影响方面,近年来取得了重大进展。......
2025-09-29
相关推荐