图3-10缩放为帧大小在“01.jpg”～“02.jpg”图片之间添加“3D运动”文件夹下的“立方体旋转”视频转场特效，直接将其拖放到两个图片之间，如图3-11所示。图3-11添加视频转场特效默认转场时间为0.24秒，单击转场，在“效果控件”面板中，通过持续时间的改变，可以设置转场的快慢，如图3-12所示。图3-13添加不同的视频转场特效新建一个静态字幕，在字幕窗口中利用“矩形工具”绘制一个黄色的矩形条，并将透明度调整为70%，如图3-14所示。......
2025-09-29
随机变量的统计参数优化
【摘要】：随机变量的概率分布完整地刻划了随机变量的统计规律。这种从侧面说明随机变量统计特性的某些特征数字，称为随机变量的统计参数。图X3.3Cv对密度曲线的影响图X3.4Cs对密度曲线的影响称Cv为样本变差系数或离势系数、离差系数，其式中，称为模比系数。
随机变量的概率分布完整地刻划了随机变量的统计规律。然而在许多实际问题中，还需要从某些侧面反映随机变量的统计特性。例如，对于年径流量，人们常常希望知道多年平均值多大，年际变化的离散程度如何等。这种从侧面说明随机变量统计特性的某些特征数字，称为随机变量的统计参数。
图X3.2 分布函数与密度函数关系示意图
统计参数有总体统计参数与样本统计参数之分。总体的统计参数与总体的分布有关，当总体未知时，总体的统计参数是未知的，只能通过样本统计参数来估计总体统计参数。
下面介绍水文计算中常用的样本统计参数。
1.样本均值
设某一随机变量的样本系列为x1，x2，…，xn，则样本的均值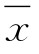
为
样本均值反映随机变量取值的平均情况，反映系列总水平的高低。例如，甲、乙两地年降水量的均值，即多年平均年降水量分别为1000mm和400mm，由此可反映两地年降水量的多寡。
设某一随机变量的样本系列为x1，x2，…，xn，则样本的均值
为
样本均值反映随机变量取值的平均情况，反映系列总水平的高低。例如，甲、乙两地年降水量的均值，即多年平均年降水量分别为1000mm和400mm，由此可反映两地年降水量的多寡。
由式（X3.12）计算的样本均值
估计总体均值是无偏估计。所谓无偏估计，是指使用式（X3.12）估计总体均值时，样本均值
总是在总体均值左右徘徊，误差可能是正的，也可能是负的，多次使用此法进行估计时，平均情况下等于总体均值。无偏估计在工程技术中称为无系统误差。
由式（X3.12）计算的样本均值
估计总体均值是无偏估计。所谓无偏估计，是指使用式（X3.12）估计总体均值时，样本均值
总是在总体均值左右徘徊，误差可能是正的，也可能是负的，多次使用此法进行估计时，平均情况下等于总体均值。无偏估计在工程技术中称为无系统误差。
需要强调指出，无偏估计的概念，只是就平均意义而言的，在总体未知的情况下，由一个具体样本算得的样本均值
是大于还是小于总体均值，是不能确定的。
2.均方差和变差系数
均值能反映随机变量取值的平均情况，但不能反映随机变量取值的离散特征。例如有两个系列：A系列：5，10，15；B系列：1，10，19。
需要强调指出，无偏估计的概念，只是就平均意义而言的，在总体未知的情况下，由一个具体样本算得的样本均值
是大于还是小于总体均值，是不能确定的。
2.均方差和变差系数
均值能反映随机变量取值的平均情况，但不能反映随机变量取值的离散特征。例如有两个系列：A系列：5，10，15；B系列：1，10，19。
两系列均值相等
＝10，且容易看出系列B的离散程度比系列A大。采用一个定量指标来衡量，引入
反映随机变量取值的离散特征，称s′为样本系列的均方差，也称为标准差。s′与随机变量的取值x的单位相同。
对于均值相同的系列，可由s′的大小判断系列离散程度的大小。s′越大，系列的离散程度越大。
容易算出，上述A、B系列的均方差分别为s′a＝4.08，s′b＝7.35。
数理统计研究表明，用式（X3.13）计算样本均方差去估计总体的均方差是系统偏小的。为纠正系统偏差要对s′进行修正，数理统计中导出修正的样本均方差的计算式为
式中，s称为修正的样本均方差，亦简称样本均方差。该式就是生产实际中样本均方差的常用计算式，用其估计总体的均方差。应该指出，对有限容量的样本由s估计总体的均方差仍系统偏小，但比s′有所改善。
对于均值不同的系列，用s比较系列的离散程度就不合适了。引入无因次数
两系列均值相等
＝10，且容易看出系列B的离散程度比系列A大。采用一个定量指标来衡量，引入
反映随机变量取值的离散特征，称s′为样本系列的均方差，也称为标准差。s′与随机变量的取值x的单位相同。
对于均值相同的系列，可由s′的大小判断系列离散程度的大小。s′越大，系列的离散程度越大。
容易算出，上述A、B系列的均方差分别为s′a＝4.08，s′b＝7.35。(https://www.chuimin.cn)
数理统计研究表明，用式（X3.13）计算样本均方差去估计总体的均方差是系统偏小的。为纠正系统偏差要对s′进行修正，数理统计中导出修正的样本均方差的计算式为
式中，s称为修正的样本均方差，亦简称样本均方差。该式就是生产实际中样本均方差的常用计算式，用其估计总体的均方差。应该指出，对有限容量的样本由s估计总体的均方差仍系统偏小，但比s′有所改善。
对于均值不同的系列，用s比较系列的离散程度就不合适了。引入无因次数
称Cv为样本变差系数或离势系数、离差系数，其式中
，称为模比系数。Cv值越大，系列的离散程度越大。Cv对密度曲线的影响如图X3.3所示。Cv越大，密度曲线形状越矮胖。对年降水量和年径流量系列来说，Cv的大小则反映了年降水量或年径流量的年际变化特征。Cv越大，年际变化越大，对水资源开发利用越不利。
3.偏态系数
引入反映随机变量取值相对于均值对称程度的特征参数，无因次数
称Cs为样本偏态系数，无因次。当Cs＝0，称为对称分布；当Cs＞0时，正离差立方和占优势，称为正偏分布；Cs＜0时，负离差立方和占优势，称为负偏分布。
图X3.3 Cv对密度曲线的影响
图X3.4 Cs对密度曲线的影响
称Cv为样本变差系数或离势系数、离差系数，其式中
，称为模比系数。Cv值越大，系列的离散程度越大。Cv对密度曲线的影响如图X3.3所示。Cv越大，密度曲线形状越矮胖。对年降水量和年径流量系列来说，Cv的大小则反映了年降水量或年径流量的年际变化特征。Cv越大，年际变化越大，对水资源开发利用越不利。
3.偏态系数
引入反映随机变量取值相对于均值对称程度的特征参数，无因次数
称Cs为样本偏态系数，无因次。当Cs＝0，称为对称分布；当Cs＞0时，正离差立方和占优势，称为正偏分布；Cs＜0时，负离差立方和占优势，称为负偏分布。
图X3.3 Cv对密度曲线的影响
图X3.4 Cs对密度曲线的影响
例如，对于系列A：3，4，5，6，7，可算得
，系列为对称分布。
例如，对于系列A：3，4，5，6，7，可算得
，系列为对称分布。
对于系列B：2，3，4，6，10，可算得
90，Cs＝1.43，系列为正偏分布。
｜Cs｜越大，随机变量的分布越偏。Cs对密度曲线的影响如图X3.4所示。例X3.2中年降水量的频率密度图呈现了明显的正偏规律。
对于系列B：2，3，4，6，10，可算得
90，Cs＝1.43，系列为正偏分布。
｜Cs｜越大，随机变量的分布越偏。Cs对密度曲线的影响如图X3.4所示。例X3.2中年降水量的频率密度图呈现了明显的正偏规律。
数理统计中可以证明正偏分布的一个结论：
。水文现象大多属于正偏分布，即Cs＞0，这说明水文变量取值大于均值的机会比取值小于均值的机会少。
用式（X3.12）～式（X3.16）计算样本参数来估计总体参数的方法称为矩法。这些公式常称为参数估计的矩法公式。除式（X3.12）估计总体均值为无偏估计外，其余各式作为总体相应参数的估值公式是系统偏小的，特别是式（X3.16）估计总体偏态系数系统偏小更为明显［2-4］。
需要指出，有些教科书中，认为式（X3.14）～式（X3.16）分别为总体均方差、变差系数、偏态系数的无偏估计公式是不正确的。
数理统计中可以证明正偏分布的一个结论：
。水文现象大多属于正偏分布，即Cs＞0，这说明水文变量取值大于均值的机会比取值小于均值的机会少。
用式（X3.12）～式（X3.16）计算样本参数来估计总体参数的方法称为矩法。这些公式常称为参数估计的矩法公式。除式（X3.12）估计总体均值为无偏估计外，其余各式作为总体相应参数的估值公式是系统偏小的，特别是式（X3.16）估计总体偏态系数系统偏小更为明显［2-4］。
需要指出，有些教科书中，认为式（X3.14）～式（X3.16）分别为总体均方差、变差系数、偏态系数的无偏估计公式是不正确的。
相关文章
- 详细阅读
-
反力弹簧参数的优化设计方法详细阅读
为了对比，采用了两组弹簧进行实验，其原长均为36mm，而刚度系数分别为根据上述仿真结果、优化设计出的2.4N/mm，和不满足设计要求的3N/mm。......
2025-09-29
-
脱扣器几何参数优化设计详细阅读
作为短路保护的电磁脱扣器对断路器的短路开断过程有重要作用，它的动作时间越短，越有利于提高短路开断性能，对塑壳断路器来说，更有利于达到操作机构动作与触头斥开过程的合理配合，防止动触头斥开后的跌落现象。所以实现电磁脱扣器的优化设计，一般可取动作时间最短作为优化的目标，而把几何尺寸作为设计变量。......
2025-09-29
-
液压泵的主要性能参数优化详细阅读
它取决于液压泵的几何尺寸,又称几何排量。液压泵的实际流量和理论流量之比称为容积效率ηbv,即式中,ηbv 为小于1 的数字,表示液压泵的内在质量的一个重要指标。液压泵的额定压力是指泵在正常工作条件下,按试验标准规定能连续运转的最高压力,它反映了泵的能力。泵的额定压力,受泵本身的零件结构强度和泄漏所限制,主要受泄漏限制。液压泵的总效率为泵的机械效率和泵的容积效率之乘积。......
2025-09-29
-
电弧喷涂工艺参数优化方案详细阅读
电弧喷涂的主要工艺参数有：喷涂电压、喷涂电流、雾化空气压力和流量、喷涂距离。由此可见，电弧电压对喷涂质量影响很大，在保证电弧稳定燃烧的前提下，应选择尽可能低的喷涂电压值。表2-7 常用材料的喷涂工作电压2.工作电流用于电弧喷涂的电源应具有平特性或略带上升的外特性，喷涂过程中，电弧电压保持不变，工作电流随送丝速度的增大而增大。......
2025-09-29
-
仿真设计：关键参数和未来事件的优化详细阅读
未来事件包括以下几种：投料事件。投料事件主要会影响仿真过程中工件信息的变化。包括设备的预维护事件、 设备的非加工占用事件等。这类事件都是在生产调度安排中已经计划的， 包括的信息是占用的设备及时间。设备已知停机事件属于系统仿真的已知事件。未知事件添加是否恰当， 会直接影响仿真结果的准确性。......
2025-09-29
-
综合成型工艺参数优化详细阅读
吹胀比2.0，牵引比为5.0，牵引速度为10～20m/min，口模间隙为0.8～1mm，常用于育秧、化肥包装等方面。吹胀比为1.5～2.5，拉伸比为2～5。各种薄膜采用的吹胀比：PVC为2.0～3.0，LDPE为1.5～3.5，LLDPE为1.5～3.0，PP为0.9～1.5，PA为1.0～1.5，HDPE超薄膜为3.0～5.0，收缩膜拉伸膜为2.0～5.0。冷冻线高度与泡型和吹胀比之间有密切关系。......
2025-09-29
-
热路参数计算方法优化详细阅读
根据式，取加热体的导热系数为λj=24.8W/（m·K），可得加热体的热阻为双金属片材料为5J20110，形状为梯形。在5.6.1中提到，为了计算的简便，在进行热路计算时仅将加热体当作唯一热源。它们共同对断路器内部零件的温升产生影响。加热体占所有热源总和的百分比为16.6%。C3=mn×cn×0.166 断路器外壳为塑料，质量mk=0.29kg，比热ck=1100J/。C4=mk×ck×0.166 电磁铁等效热路的热容的单位为J/K。......
2025-09-29
相关推荐