首页理论教育PCA的理论原理和推导过程

PCA的理论原理和推导过程

2023-06-21 理论教育版权反馈

【摘要】：图10－1PCA推导在图10－1中，u1就是主成分方向，然后在二维空间中取与u1方向正交的方向，就是u2的方向。则n个数据在u1轴的离散程度最大，即方差最大，数据在u1上的投影代表了原始数据的绝大部分信息，即使不考虑u2，信息损失也不多。PCA有两种通俗易懂的解释:①最大方差理论；②最小化降维造成的损失。如图10－1所示，样本在u1上的投影方差较大，在u2上的投影方差较小，那么可认为u2上的投影是由噪声引起的。

假设有二维数据，即只有两个变量，它们由横坐标和纵坐标所代表，如图10－1所示，因此每个观测值都有相应于这两个坐标轴的两个坐标值；如果这些数据形成一个椭圆形状的点阵，那么这个椭圆有一个长轴和一个短轴，在短轴方向上，数据变化很小；如果在极端的情况，短轴退化成一点，那只有在长轴的方向才能够解释这些点的变化，这样由二维到一维的降维就自然完成了。

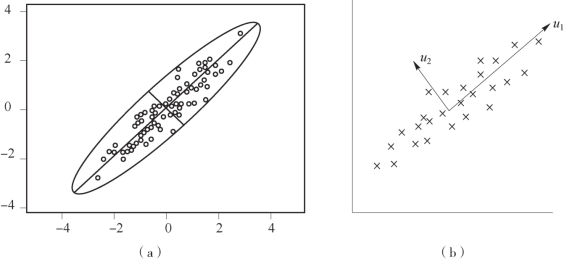
pagenumber_ebook=146,pagenumber_book=136

图10－1　PCA推导

在图10－1中，u1就是主成分方向，然后在二维空间中取与u1方向正交的方向，就是u2的方向。则n个数据在u1轴的离散程度最大，即方差最大，数据在u1上的投影代表了原始数据的绝大部分信息，即使不考虑u2，信息损失也不多。而且u1，u2不相关。只考虑u1时，二维降为一维。

PCA有两种通俗易懂的解释:①最大方差理论；②最小化降维造成的损失。这两个思路都能推导出同样的结果，这里只介绍最大方差理论。

在信号处理中认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，越大越好。如图10－1所示，样本在u1上的投影方差较大，在u2上的投影方差较小，那么可认为u2上的投影是由噪声引起的。

因此我们认为，最好的k维特征是将n维样本点转换为k维后，每一维上的样本方差都很大。例如，将图10－2中的5个点投影到某一维上，这里用一条过原点的直线表示(数据已经中心化)。

pagenumber_ebook=147,pagenumber_book=137

图10－2　两种不同方式的投影图

假设选择两条不同的直线做投影，那么左右两条中哪个好呢?根据之前的方差最大化理论，左边的好，因为投影后的样本点之间方差最大，也可以说是投影的绝对值之和最大。计算投影的方法如图10－3所示。

pagenumber_ebook=147,pagenumber_book=137

图10－3　投影的方法

在图10－3中，小点表示样例，大点表示在u上的投影，u是直线的斜率也是直线的方向向量，而且是单位向量。大点是在u上的投影点，离原点的距离是＜x，u＞。