基于高斯混合模型的聚类算法：期望最大化

2023-06-21 理论教育版权反馈

【摘要】：图9－4K－Means不适用的情况高斯混合模型具有比K－Means更好的灵活性。使用GMM，需要假设数据点是高斯分布，相对于环形的数据而言，这个假设的严格程度与均值相比弱很多。因此，每个高斯分布会被分配到单一的聚类簇。基于这些概率，我们为高斯分布计算了一组新的参数，这样就可以最大化集群中数据点的概率。

K－Means的一个主要缺点是它简单地使用了集群中心的平均值。如图9－4所示，可以看到为什么这不是最好的方式。图片的左半边，可以很明显地看到，有两个半径不同的圆形星团以相同的平均值为中心。K－Means不能处理这个问题，因为不同簇的平均值非常接近。当簇不是圆形时，K－Means也会失效，这也是将均值用作簇中心的后果。

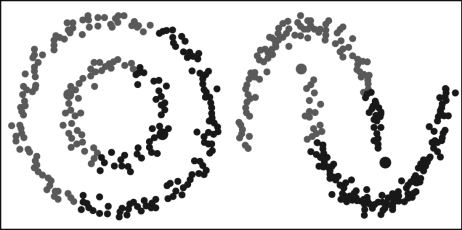
pagenumber_ebook=138,pagenumber_book=128

图9－4　K－Means不适用的情况

高斯混合模型(Gaussian Mixture Models，GMM)具有比K－Means更好的灵活性。使用GMM，需要假设数据点是高斯分布，相对于环形的数据而言，这个假设的严格程度与均值相比弱很多。这样的话，有两个参数来描述簇的形状:均值和标准差。以二维为例，意味着簇可以是任何一种椭圆形(因为有两个标准差在x和y方向)。因此，每个高斯分布会被分配到单一的聚类簇。

为了在每个聚类簇中找到这两个高斯参数(均值和标准差)，将使用的优化算法称为期望最大化(Expectation－Maximization，EM)算法。

算法9.4　EM算法

(1)首先设定聚类簇的数量(如K－Means)；然后随机初始化每个集群的高斯分布参数，也可以通过快速查看数据来为初始参数提供一个很好的猜测。

(2)给定每个簇的高斯分布，计算每个数据点属于特定簇的概率。一个点越靠近高斯中心，它就越可能属于该簇。这应该是直观的，因为对于高斯分布，假设大多数数据都靠近集群的中心。

(3)基于这些概率，我们为高斯分布计算了一组新的参数，这样就可以最大化集群中数据点的概率。使用数据点位置的加权和计算这些新参数，其中权重是属于特定集群的数据点的概率。

(4)重复第(2)步和第(3)步，直到收敛，也就是在收敛过程中迭代变化不大。

使用GMM有两个关键优势。首先，GMM在簇协方差方面比K－Means灵活得多；由于标准偏差参数的存在，簇可以呈现任何椭圆形状，而不局限于圆形。K－Means实际上是GMM的一个特例，其中每个簇的所有维的协方差都接近于0。然后，由于GMM使用概率，因此每个数据点可以有多个集群。因此，如果一个数据点位于两个重叠集群的中间，我们可以简单地定义它的类，方法是它属于类1的概率是X%，属于类2的概率是Y%，即GMM支持混合成员。

基于高斯混合模型的聚类算法：期望最大化

相关推荐