Spark MLlib中的K-means算法使用Map分布式读取数据集，并存储在内存里。计算时，用Map键值对表示随机挑选出来的k个聚类中心，Spark的驱动器节点负责把数据发送到各个工作节点，以实现具体的计算任务。Spark MLlib不同于传统的机器学习工具，它提供了简单易用的API，特别是Spark能够高效地处理大数据，并且在迭代计算时具有较强的优势。......
2023-11-21
基本概念：DBSCAN密度聚类算法
【摘要】：图9－2DBSCAN基本概念(见彩插)图9－3“直接密度可达”和“密度可达”概念示意描述根据前面基本概念的描述知道:由于有标记的各点M、P、O和R的Eps近邻均包含三个以上的点，因此它们都是核对象；M是从P“直接密度可达”；而Q则是从M“直接密度可达”；基于上述结果，Q是从P“密度可达”；但P从Q无法“密度可达”(非对称)。
(1)Eps邻域:给定对象半径Eps内的邻域称为该对象的Eps邻域。
(2)核心点:如果对象的Eps邻域至少包含最小数目minPts的对象，则称该对象为核心对象。
(3)边界点:边界点不是核心点，但落在某个核心点的邻域内。
(4)噪声点:既不是核心点，也不是边界点的任何点。
(5)直接密度可达:给定一个对象集合D，如果p在q的Eps邻域内，而q是一个核心对象，则称对象p从对象q出发时是直接密度可达的。
(6)密度可达:如果存在一个对象链p1，…，pi，…，pn，满足p1＝p和pn＝q，pi是从pi＋1关于Eps和minPts直接密度可达的，则对象p是从对象q关于Eps和minPts密度可达的。
(7)密度相连:如果存在对象O∈D，使对象p和q都是从O关于Eps和minPts密度可达的，那么对象p到q是关于Eps和minPts密度相连的。
(8)类:为非空集合，满足密度可达且密度相连。
有关核心点、边界点、噪声点以及直接密度可达、密度可达和密度相连解释如图9－2所示。
图9－2中的红色为核心点，黄色为边界点，蓝色为噪声点，minPts＝4，Eps是图中圆的半径大小。有关“直接密度可达”和“密度可达”定义的实例如图9－3所示。其中，Eps用一个相应的半径表示，设minPts＝3。
图9－2 DBSCAN基本概念(见彩插)
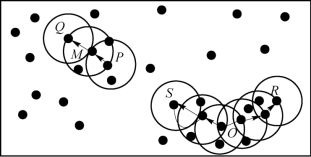
图9－3 “直接密度可达”和“密度可达”概念示意描述
根据前面基本概念的描述知道:由于有标记的各点M、P、O和R的Eps近邻均包含三个以上的点，因此它们都是核对象；M是从P“直接密度可达”；而Q则是从M“直接密度可达”；基于上述结果，Q是从P“密度可达”；但P从Q无法“密度可达”(非对称)。类似地，S和R从O是“密度可达”的；O、R和S均是“密度相连”(对称)的。
有关数据挖掘技术与应用的文章
- 详细阅读
-
Mean-Shift聚类算法详解详细阅读
Mean－Shift聚类是一个基于滑窗的算法，其目的是尝试找到数据点密集的区域。算法9.2M ean－Shift聚类确定滑动窗口半径r，以随机选取的中心点为C、半径为r的圆形滑动窗口开始滑动。Mean－Shift聚类的优点如下:不同于K－Means算法，均值漂移聚类算法不需要知道有多少类/组。基于密度的算法相比于K－Means受均值影响较小。Mean－Shift聚类的缺点:窗口半径r的选择可能是不重要的。......
2023-06-21
-
聚类算法与特异性发现算法的比较详细阅读
聚类分析发现强相关的对象组，而特异检测发现不与其他对象强相关的对象。图3.8K-means聚类方法与CpecuFind发现特异数据能力ROC曲线K-means聚类；CpecuFind表3.6K-means与CpecuFind发现特异数据能力ROC曲线面积对比上述对比说明，只简单地以簇类大小和对象与类心距离来评估对象的特异程度结果很粗糙，其评价特异数据的能力远不如Cpecu Find方法。......
2023-06-16
-
K-Means 聚类算法优化简介详细阅读
算法9.1K－Means聚类选择一些类/组，并随机初始化它们各自的中心点，中心点是与每个数据点向量长度相同的位置。K－Means采用的启发式方式很简单，用下面一组图就可以形象地描述。图9－1K－Means的启发式方式(见彩插)......
2023-06-21
-
基于RNN的层次聚类算法介绍详细阅读
RNN算法对标准层次聚类的合并准则和相似度度量做了相应的改进，从而降低了其复杂度，使其更适用于大规模的数据集。当合并最近邻对得到一个新的簇时，需要重新计算该簇与其他各个簇的相似度，如果通过平均值的距离来度量两个簇的距离，其计算复杂度仅为O，但是由于本书采用的是平均距离，则需要通过更为有效的方法进一步降低复杂度。对于低维数据，还可以通过更为有效的最近邻搜索技术进一步降低复杂度。......
2023-06-28
-
基于聚类的全局特异数据挖掘算法详细阅读
设某一属性的所有值的数据集为S，其平均值为Smean。根据这些想法，提出一种基于聚类的全局特异数据挖掘方法。构架仍由挖掘特异属性和挖掘特异记录两个层次构成。从原则上讲可以采用任何基于距离的聚类算法对S进行聚类，采用的聚类算法的效果好，可以减少后续的计算量。图3.2SimC聚类算法可以看出，k是控制聚类半径Cd的。现在根据式（3.9）计算每个类的特异因子，记为CPF。显然，CPF越小的类，其中的元素是特异数据的可能性越小。......
2023-06-16
-
基于高斯混合模型的聚类算法：期望最大化详细阅读
图9－4K－Means不适用的情况高斯混合模型具有比K－Means更好的灵活性。使用GMM，需要假设数据点是高斯分布，相对于环形的数据而言，这个假设的严格程度与均值相比弱很多。因此，每个高斯分布会被分配到单一的聚类簇。基于这些概率，我们为高斯分布计算了一组新的参数，这样就可以最大化集群中数据点的概率。......
2023-06-21
-
DBSCAN算法的原理及优化探究详细阅读
DBSCAN通过检查数据集中每点的Eps邻域来搜索簇，如果点p的Eps邻域包含的点多于minPts个，则创建一个以p为核心对象的簇。DBSCAN迭代地聚集从这些核心对象直接密度可达的对象，这个过程可能涉及一些密度可达簇的合并。当没有新的点添加到任何簇时，该过程结束。算法9.3DBSCAN算法输入:数据集D；给定点在邻域内成为核心对象的最小邻域点数:minPts；邻域半径:Eps；输出:簇集合。标记所有对象为unvisited。重复步骤～，直至没有标记为unvisited的对象。......
2023-06-21
相关推荐