目前,能够用于大容量储能的蓄电池类型只有铅酸蓄电池。此外,铅酸蓄电池的放电深度不能低于其额定容量的80%,超过80%的放电深度会缩短电池的寿命。研究人员正在试图改进这种蓄电池的性能。尽管镍镉蓄电池具有良好的电气性能,但其市场份额并不大。尽管环境温度65℃时,电池的内部温度高达95℃,且放电结束时,电池温度可达160℃,但电池依然能安全运行、结构完好。......
2023-06-23
1.静态经济分析
静态经济分析的评价指标为投资回收期N。投资回收期定义为投建该储能系统比参照系统所增加的投资费用(ΔCOST)与该储能系统投运后每年节约的运行费用(ΔSaving)的比值,即

式中,ΔCOST=COSTbess-COSTref;ΔSaving=Chargeref-Chargebess。其脚注bess表示电池储能系统的投资成本和能耗支出;ref表示参比系统的投资成本和能耗支出。在投资回收年限之后,其每年节省的运行费用则为用户净收益。
该方法适用于短期回收工程,如N≤5年。静态评估方法简单而直观,可用于筛选并列的几种替代方案,例如在电池储能系统应用中,关于电池种类锁定铅酸电池、钠硫电池还是全钒电池的问题。
2.动态投资回收期法
在涉及动态投资的经济评估中,除了考虑系统初始投资和运行维护费用,还考虑到时间价值的影响,包括通货膨胀率、利率以及贴现率等。设储能系统投用后收益为NPVbess,而投资成本以及运行支出为NPVcost,则利润为
Profit=NPVbess-NPVcost(5-14)


式中,T表示储能系统的服务年限;r表示考虑投资时间价值的贴现率;Reven-uebess表示储能系统的年收益;COSTbess表示储能系统的年支出。将式(5-15)、(5-16)代回式(5-14),可根据收支平衡原则确定回收期,计算方法如下:
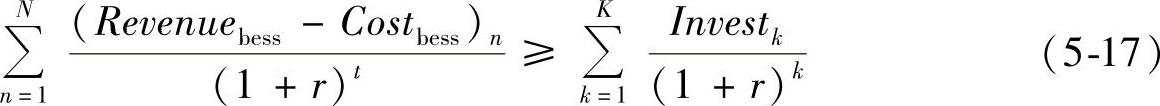
式中,N为动态投资回收年限,K为投资结束的年限;r为贴现率;Investk为第k年的追加投资;Profitn=(Revenuebess-Costbess)n为第n年的净收益。由式(5-17)即可得到关于N的表达式。
3.寿命周期分析法
寿命周期分析法是从储能系统使用寿命周期的角度进行经济分析的。寿命周期投资包括系统服务期内所有的投资费用、建筑能耗费用、设备追加及维修、安装及材料更换等,以及其他与投资相关的费用。在该方法中,所有资金量都要考虑与当前资金的等价性,均需转换成当前净资金(Net Present Value,NPV),即净现值NPV。

式中,COSTinital表示储能系统的初始一次性投资;其他同上。当NPV>0时说明该方案可行。若多个并列方案横向对比,在使用寿命T相同的前提下,NPV最大的方案为最优。
无论采用哪种经济分析方法,其结果必然存在误差。成本评估误差通常源于两种原因:
1)厂商知晓但拒绝公开的价格信息。这部分往往被视作商业机密或私有资产,包括机密原材料、特有的制作方法、加工成本以及将来预期的批量生产的成本降幅。
2)厂商和相关部门都无法确定的信息。例如原材料将来随市场价格的波动以及有待开发的新兴材料成本等。
4.实物期权法
实物期权方法可用于研究不确定环境下的投资决策问题,反映决策灵活性和不确定性的价值,弥补静态经济分析方法的不足。实物期权定价的二叉树分析方法由John Cox、Stephen Ross和Mark Rubinstein提出,通常采用连续时间的Black-Scholes模型或离散时间的二叉树模型(见图5-58)。考虑投资决策的不确定性,将期权的有效期间分为若干个时间间隔,根据资产价值S的波动情况,确定资产价值在各时间间隔的上涨幅度和下跌幅度、资产运动的上升概率和下降概率,建立资产变化的树形图,最后通过树形图倒推,计算实物期权的价值C。综合分析项目的实物期权价值和项目投资的净现值NPV评价项目投资的经济性问题。
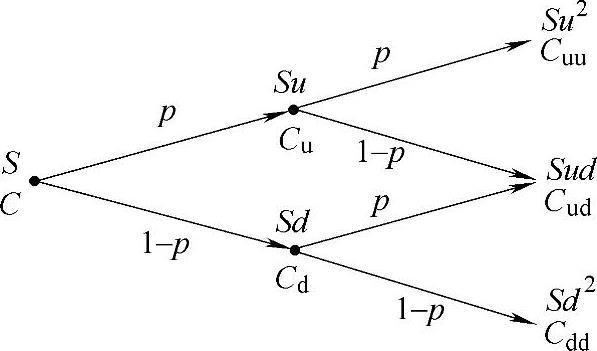
图5-58 二叉树分析模型
上涨幅度、下跌幅度、上升概率由风险中性定价原理得出,如下



式中,r代表无风险利率,在整个投资项目寿命期内,视为常数;σ为资产回报率的瞬时标准差,假定为常数;u和d分别代表标的资产价值在各区间上升和下降的幅度;Δt为时间间隔;p代表标的资产价值在各区间上升的概率;C代表期权的价值。
实物期权价值C的求解。假设在t0时刻有一项目投资机会,其期权价值为C1,到期日是t1时刻,t1时刻C1的执行(执行价格是I1)将产生现金流价值V1,若t2时刻有另一项目投资机会,在t1时刻其实物期权的价值为C2,依此类推。为便于理解,可参考图5-59。
第一阶段的标的资产价值C1是C2和V1的总和,价值V1在C1的有效期[t0,t1]内以概率p变为uV1,或者以概率1-p变为dV1,从而根据二叉树定价方法和风险中性的定价原理,可以得出在第一阶段的期初t0时刻的价值C1为
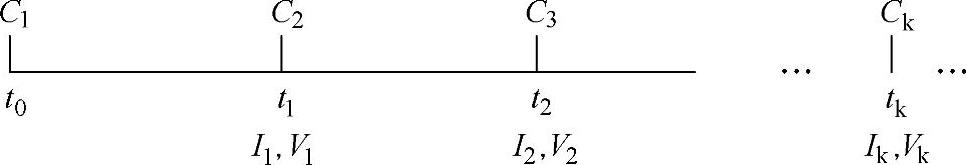
图5-59 实物期权示意图
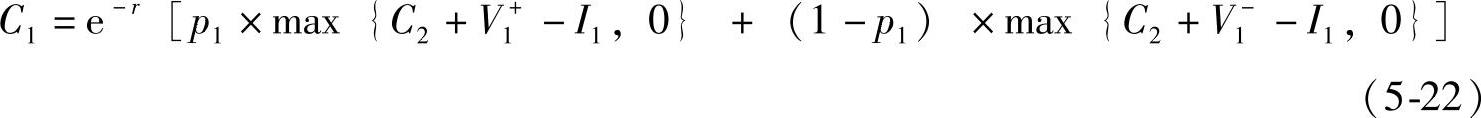
有关智能电网中的风光储关键技术的文章

目前,能够用于大容量储能的蓄电池类型只有铅酸蓄电池。此外,铅酸蓄电池的放电深度不能低于其额定容量的80%,超过80%的放电深度会缩短电池的寿命。研究人员正在试图改进这种蓄电池的性能。尽管镍镉蓄电池具有良好的电气性能,但其市场份额并不大。尽管环境温度65℃时,电池的内部温度高达95℃,且放电结束时,电池温度可达160℃,但电池依然能安全运行、结构完好。......
2023-06-23

电池储存电能的能量块手机可以帮助我们和朋友保持联系;电子表可以向我们通报时间;手电筒可以帮助我们在黑暗中照亮,而这些物品的工作都离不开电池的有力支撑。应用在手机上的锂电池电动自行车上的铅酸电池作为储存电能的能量块,电池已经诞生了200多年,并且现在仍然在不断改进,在现代科技中,电池扮演的角色越来越不可或缺。伏打电池在伏打电池发明之前,人们只能使用储存在莱顿瓶中的电。......
2024-06-12

表1-2给出了一份总结。事实上,由于储能系统的高成本,其经济效益尚未被充分证实,也没有得到广泛认可。表1-2 储能在电力系统中的可能应用(续)需要特别说明的是,在今天或可预见的未来,认识到某些因素的影响,进而评估储能的经济性是非常必要的。最后,在储能系统自身的经济效益尚不可观时,需要考虑其他具有竞争性的解决方案及其可能的发展态势。......
2023-06-22

以储能提高风电接纳能力为例,分析风电场中配置储能系统的经济效益。假定在该风电场中规划建设5MW/10MW·h储能系统,使用寿命T=20年,EEES=7200MW·h,Rout=0.61元/kW·h,Ccoal=0.32823元/kW·h,常规燃煤发电的环境成本为0.109186元/kW·h,分析三种储能系统的经济效益。表5-6 算例经济分析结果统计由表5-6可知,目前的储能系统成本及收益水平下,锂离子电池的投资经济性优于全钒液流电池、钠硫电池。......
2023-06-20

锂电池是近年来发展迅猛的一种新能源产品。图4-6-1锂电池三视图包装的功能就是在流通过程中保护产品、方便储运、促进销售。其防护能力是对包装最基本的要求,该锂电池对外力的承受能力较差,在选择防震包装时,需要使用刚度小的材料,使得包装具有缓冲和防震功能。由于该锂电池的质量为50kg,装卸工具选择叉、吊车,在装卸时,要保证内外包装牢固可靠,适合长途运输、起吊、托运等要求。......
2023-06-27

极端情况下,电力系统会变得不稳定。众所周知,现有的电力系统在电力产量和负载需求之间缺少密切的相关性。美国曾在20世纪发现,如果将6%~12%的发电容量作为能量储存系统安装,那么电网的运行将是最高效的。输入功率和释放功率的大小则与能量转换器的特性有关。换句话说,采用的储能装置和能量转换器的特性决定了能量储存的动态特性。......
2023-06-23

在特定条件和特定运行模式下,燃料电池可以形成水自足系统。图7-1 燃料电池系统为了能够体现这些附属装置对燃料电池性能的显著影响,我们以当前最为普遍的质子交换膜燃料电池为例,说明此类燃料电池系统中不同的附属装置的典型能量消耗情况,如图7-2所示。图7-2强调了燃料电池系统中不同的附属装置对系统动态性能及效率的重要性和影响。本章的最后还将分析燃料电池系统的寿命和失效机理。......
2023-06-22

目前比较典型的电池管理系统有美国AC Propulsion 公司的BATOPT 系统、Aerovironment 公司的SmartGuard 系统、通用公司EVI 电池管理系统以及近几年以来比较火热的特斯拉电动汽车电池管理系统。美国通用公司研发的EVI 电池管理系统利用微处理器对26 块串联而成的铅酸蓄电池组进行监控,从而获取电池组信息,估算电池的荷电状态。德国在汽车制造业方面一直独树一帜,在电池管理系统方面比较有名的有BADICHEQ 系统、BADICOACH B系统和BATTMAN 系统。......
2023-09-28
相关推荐