在输出波形不失真的条件下，选取适当幅度的正弦输入信号，在维持输入信号幅度不变的情况下，逐点改变输入信号频率。测量输出电压，记入表2.8.1中，描绘频率特性曲线。表2.8.12.二阶高通滤波器实验电路如图 2.8.3所示。测绘高通滤波器的幅频特性曲线，记入表2.8.2。实测电路的中心频率f0。测绘电路的幅频特性，记入表 2.8.4。......
2023-06-26
BET法测定比表面积的测量原理与实验步骤
【摘要】：图9-6典型的BET作图实际测试过程中，通常实测3～5组被测样品在不同氮气分压下多层吸附量，得到一系列不同压力下的P和吸附气体的体积值。所以BET法测定比表面积的关键是测出V值。
吸附现象的描述除了采用上述的等温线外，有些吸附现象可以用数学方程来描述。描述吸附现象比较重要的数学方程有Langmuir等温方程、BET吸附等温方程、Freundich等温方程和Temkin等温方程。其中，最常用的是BET吸附等温方程。利用氮吸附可以测量纳米材料的比表面积和孔材料的孔径分布。它们都是利用等温吸附曲线进行计算，只不过计算依据根据吸附的类型而有所变化。
1.比表面积测定法
BET氮吸附测定比表面积的基本原理是根据Branauer、Emmett和Teller三人提出的多分子层吸附模型，并推导出单层吸附量Vm与多层吸附量之间的关系，即著名的BET方程
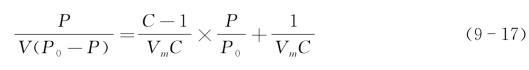
式中，P和P0分别为平衡吸附压力和吸附温度下氮气的饱和蒸汽压（Pa）；V和Vm分别为吸附体积和单分子层吸附体积，mol／g；C是与吸附热和冷凝热有关的常数。
由上式可以看出，BET方程建立了单层饱和吸附量Vm与多层吸附量V之间的数量关系，为比表面积测定提供了很好的理论基础。BET方程是建立在多层吸附的理论基础之上，与物质实际吸附过程更接近，因此测试结果更准确。可测定样品范围广，测试结果准确性和可信度高，特别适合科研及生产单位使用。在实际中，通过测量吸附在固体表面（包括固体最外部的表面和气体可到达的孔的内表面）的气体的量，计算出固体单分子层的吸附体积Vm，利用式10-17即可得到材料的比表面积。
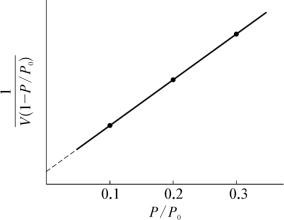
图9-6 典型的BET作图
实际测试过程中，通常实测3～5组被测样品在不同氮气分压下多层吸附量，得到一系列不同压力下的P和吸附气体的体积值（P，V值）。以
作曲线，得到斜率值
和截距值
（如图9-6所示）。理论和实践表明，当P／P0取点在0.05～0.35范围内时，BET方程与实际吸附过程相吻合，图形线性也很好，因此实际测试过程中选点在此范围内。因为
于是得到Vm值，即单层饱和吸附体积（铺满单层时的体积）。把Vm换算为吸附质分子数（Vm／V0）NA，乘以一个吸附分子的截面积Am，单位体积比表面积的计算公式为
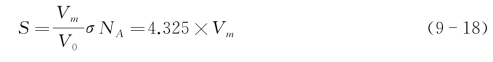
式中，S为单位体积比表面积；σ为氮分子的横截面积，16.2×10-20 m2（77 K）；NA是阿伏伽德罗常数，6.022×1023 mol-1，V0为气体的摩尔体积。
当吸附气体为氮气时，S=4.25Vm。
所以BET法测定比表面积的关键是测出V值。由于选取了3～5组P／P0进行测定，通常我们称之为多点BET。当被测样品的吸附能力很强，即C值很大时，直线的截距接近于零，可近似认为直线通过原点，此时可只测定一组P／P0数据与原点相连求出比表面积，我们称之为单点BET。与多点BET相比，单点BET结果误差会大一些。若采用流动法来进行BET测定，测量系统需具备能精确调节气体分压P／P0的装置，以实现不同P／P0下吸附量测定。对于每一点P／P0下，BET吸脱附过程与直接对比法相近似，不同的是BET法需标定样品实际吸附气体量的体积大小，而直接对比法则不需要。
BET公式也具有它的局限性，只适用于Ⅱ、Ⅳ型吸附等温线。常数C与吸附能量相关：C=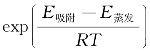
，C值必须为正值。一般而言，对于有机物、高分子和金属，C=2～50；对于氧化物，C=50～200；对于活性碳和分子筛C≥200。BET理论是建立在纳米孔和较大孔材料基础上的，在研究以微孔为主的样品的比表面积时，BET公式并不适用，计算出的比表面积有较大的误差。
2.孔径（孔隙度）分布测定
气体吸附法孔径（孔隙度）分布测定利用的是毛细凝聚现象和体积等效代换的原理，即以被测孔中充满的液氮量等效为孔的体积。吸附理论假设孔的形状为圆柱形管状，从而建立毛细凝聚模型。由毛细凝聚理论可知，在不同的P／P0下，能够发生毛细凝聚的孔径范围是不一样的，随着P／P0值增大，能够发生凝聚的孔半径也随之增大。对应于一定的P／P0值，存在一临界孔半径Rk，半径小于Rk的所有孔皆发生毛细凝聚，液氮在其中填充，大于Rk的孔皆不会发生毛细凝聚，液氮不会在其中填充。临界半径可由凯尔文方程给出
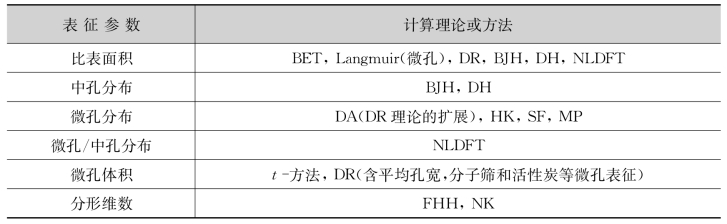
Rk称为凯尔文半径，它完全取决于相对压力P／P0。凯尔文公式也可以理解为对于已发生凝聚的孔，当压力低于一定的P／P0时，半径大于Rk的孔中凝聚液将气化并脱附出来。理论和实践表明，当P／P0大于0.4时，毛细凝聚现象才会发生，通过测定出样品在不同P／P0下凝聚氮气量，可绘制出其等温吸脱附曲线，通过不同的理论方法可得出其孔容积和孔径分布曲线。相关理论包括DR方程、HK方程及其相关改进公式、密度函数法（DFT）和BJH法。最常用的计算方法是利用BJH理论，通常称之为BJH孔容积和孔径分布。表9-1列出了具体参数及相关的计算方法，但对于不同的材料来说，并不是所有的计算公式都适用。
表9-1 氮吸附可表征的参数及其相关的计算理论
有关纳米材料与结构测试方法的文章
- 详细阅读
-
实验内容与步骤详细阅读
将 74LS00 的 14 脚接高电平，7 脚接地，按表 3.1.1 要求改变 A、B 状态，观察 Y 状态变化，测试结果记入表 3.1.1。图3.1.274LS02管脚图排列图表3.1.23.异或门逻辑功能测试将74LS86 按图3.1.3接线，输入端1、2、4、5接电平开关，输出端A、B、C接电平显示发光二极管。图3.1.374LS86连接图将电平开关按表3.1.3置位，将结果填入表中。图3.1.474LS00连接图表3.1.45.平均传输延迟时间tpd的测试（选做）用六反相器74LS04按图3.1.5接线，观察电路输出波形，并测量反相器的平均传输延迟时间。......
2023-06-26
-
准备实验硬件条件的方法与步骤详细阅读
但现场情况复杂多变，有时气体未进入超临界状态。图6-8 在注塑机上加装的部件注气装置对实验十分重要，准备实验的初期，考虑到实验工艺过程的复杂性，制作了定量非连续注气系统，其基本原理是设置一个定量罐，在一次注塑周期中将定量罐中的气体注入注塑机机筒中，以简化注气工艺，图6-9为实物。上列5～9处为输入注气装置的控制系统。......
2023-07-02
-
大学物理实验不等精度测量|测量结果不同详细阅读
，Nk，如果每次测量的条件不同，那么这些值的精确程度不能认为是相同的。在这种情况下，所进行的一系列测量称为不等精度测量。例如，同一实验者用精度不同的3种天平称量某一物体质量m ，得到3个值m1、m2、m3，或者用3种不同的方法测量某一物质的密度ρ，得3个值ρ1、ρ2、ρ3，这都是不等精度测量。......
2023-11-02
-
测量员入门：水平角度测量步骤与技巧详细阅读
第一个目标A：置零第二个目标B：水平角度（α）=39°43′20″水平角度测量流程如图9-37所示。图9-37 测量两方向间水平角图9-38 垂直角度测量图9-39 重复测量流程4.利用视距丝测距利用仪器望远镜分划板视距丝以及标尺可进行测距；具体步骤如下：在测站安放并整平仪器。通过望远镜观察，确定分划板上下视距丝分别在标尺上对应的读数，从而确定在标尺上截取的间隔“l”。......
2023-08-20
-
电极电位的测量与原理解析详细阅读
在1.1节的基本概念里，已经了解了电极是指金属与电解液组成的体系，即电子导体和离子导体组成的体系。然而，绝对电极电位无法测量，必须借助于参比电极与该电极组成原电池，才能通过仪器测量原电池的电动势来得到。......
2023-06-23
-
半圆盘弯曲实验的步骤详细阅读
根据研究发现，半圆盘弯曲实验测量结果重复性较好，是一种适用于评价复合材料弯拉强度的简单实验方法［6，7］。研究者在半圆盘弯曲实验试样的受力状态研究中，发现公式中的应力系数有的比较接近，有的相差甚远。目前，适合的测量炸药材料拉伸性能的方法并不多，因此采用半圆盘弯曲实验研究炸药拉伸力学性能的方法有很大研究空间。......
2023-06-27
-
冲击测量法：原理与应用详细阅读
图8-5磁化曲线测量原理图［1］冲击测量法还可用于测量材料的磁化曲线和磁滞回线。测量时选用环形样品以避免退磁场对磁化的影响。磁化线圈W1的匝数较多，与直流电源相连接，用于产生较强的磁场；测量线圈W2匝数较少，与冲击检流计相串联，用于产生感应电势，形成一个测量回路。如前所述，磁感应强度B可表述为式中，N为测量线圈W2的匝数；S为样品的截面积；Cμ为测量回路的冲击常数；αm为冲击检流计灯尺上的最大偏格数。......
2023-06-20
相关推荐