纳米压痕仪不仅能测量传统的硬度指标，也可以测量拉伸指标、冲击指标等，因此得到了广大纳米科技工作者的青睐。纳米压痕仪作为一种高精度的压痕测试设备，其载荷精度已达到几十个纳牛顿，位移精度达到0.1 nm，可以精确地完成量程为数十个纳米的压痕实验，形成了纳米压痕测量技术。图6-13纳米压痕仪全貌图局部放大图本章介绍的纳米压痕仪是指广义的纳米压痕仪，也可称作纳米力学测试系统。......
2023-06-20
探究纳米压痕测试的原理
【摘要】：图6-14弹塑性材料在纳米压痕实验中的压痕变化剖面图图6-15典型的纳米压痕实验载荷位移曲线1.压痕硬度和弹性模量的计算在图6-15中，hmax表示测试时的最大压痕深度，Pmax表示测试时的最大加载力，hf表示卸载后的剩余压痕深度。纳米压痕仪不仅仅可以测得纳米材料的杨氏模量，还可以测得纳米材料的硬度。
为了便于理论分析，通常用一个轴对称压头作为纳米压痕试验的理论模型，图6-14为试验过程中压痕剖面变化的示意图。当压头压入样品后，压头附近的材料首先产生弹性变形，随着载荷的增加，样品开始产生塑性变形，样品中出现一个与压头形状匹配的压痕，压痕的接触深度为hc，接触圆半径为a。当压头卸载时，仅仅弹性变形得到恢复。
压痕实验中，通过分析加载—卸载的循环过程，记录载荷—位移数据，再根据相关的力学模型，计算出压头与材料的接触面积等参数，即可测量材料的硬度和弹性模量等参数。因此，在解释硬度和弹性模量的计算公式之前，需要对载荷—位移曲线进行分析。图6-15是一个典型的加载—卸载循环过程的载荷—位移曲线。从图6-15可以看到，加载和卸载过程的位移随载荷的变化不是重合的。这是因为在加载过程中，材料除了产生弹性变形外，还会产生塑性变形，而在载荷卸载时，只有弹性变形能够恢复。因此，加载曲线反映的是材料的弹塑性变形过程；卸载曲线反映的是材料的弹性回复过程；经过一个加载—卸载循环过程最终形成的残余应力反映了材料的塑性变形。
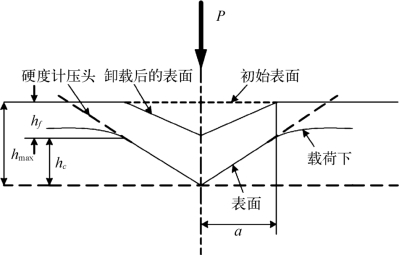
图6-14 弹塑性材料在纳米压痕实验中的压痕变化剖面图
图6-15 典型的纳米压痕实验载荷位移曲线
1.压痕硬度和弹性模量的计算
在图6-15中，hmax表示测试时的最大压痕深度，Pmax表示测试时的最大加载力，hf表示卸载后的剩余压痕深度。根据传统的Olive-Pharr压痕实验研究［62］，在最大加载力处，沿压痕曲线的卸载部分做一条切线，我们可以把该直线的斜率定义为初始点的卸载刚度S，其具体的定义表达式为
式中，A为压痕印迹的投影接触面积，E*为简约化的等效弹性模量（杨氏模量），其与被测样品品和压头的弹性模量有关；β为与压头几何形状有关的常数，如具有圆形截面的圆锥和球形压头，则β与压头，其他形状压头的β值见表6-1。被测材料的弹性模量可从下式计算得出
式中，E和ν分别为样品的弹性模量和泊松比，Ei和υi分别为压头的弹性模量和泊松比，为已知量。对于金刚石材质的压头，压头的弹性模量和泊松比分别为Ei=1 141 GPa，νi=0.07。由式（6-6）和式（6-7）即可计算出所测材料的弹性模量。
纳米压痕仪不仅仅可以测得纳米材料的杨氏模量，还可以测得纳米材料的硬度。硬度作为一个表征材料坚韧程度的力学参数，其物理意义在于反映材料抵抗外物压入其表面的能力。对于纳米压痕实验来说，被测纳米材料的硬度H可以表示为［63］
式中，Pmax为最大载荷；A为压痕印迹的投影接触面积，是压痕接触深度的函数，且与压头的形状有关。在理想情况下，当压头的形状为Berkovich压头时，A可以由下式来表达
式中，hc为压痕接触深度。式6-9仅仅是相对于理想情况而言的，在实际情况下，一般需要对其进行修正。根据经验方法，我们可以把压痕印迹的投影接触面积的计算公式修正为［64］
式中，C1=24.56，参数C2、C3、C4等的具体数值可以通过拟合得到。压痕接触深度hc的表述见图6-14，具体数值可以由下面的公式获得
式中，ε的取值是与所用的压头形状有关。对于平直圆柱型压头、旋转抛物线型以及Berkovich压头，ε的值分别取1.0、0.75、0.75［65］。
2.Martens硬度
Martens硬度是在压痕试验中载荷达到规定的试验力后，试验力除以压头压入样品表面后的压痕表面积，单位为N／mm2。
测Martens硬度的压头有两种，维氏压头和Berkovich压头，采用维氏压头时
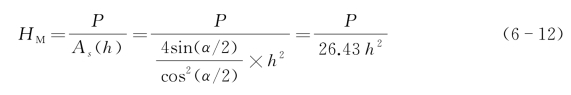
当采用Berkovich压头时
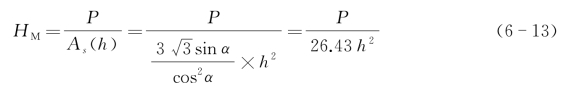
为了便于比较，试验力应选择1 N、2.5 N和5 N以及它们的十或十分之一倍数，试验力有时还应在最大力时保持一定的时间。Martens硬度包含有弹性和塑性变形，它适合于所有的材料。
3.压痕蠕变CIT
载荷保持一定，随着温度的增加，材料会发生随时间不同，变形也不同的现象，这种现象叫做蠕变。材料在恒载荷的情况下，压痕深度的相对变化量就为压痕蠕变CIT，即
式中，h1为开始保持载荷时的压痕深度（单位mm）；h2为保持载荷结束时的压痕深度（单位mm）。压痕蠕变与传统上的拉伸蠕变是不同的，在拉伸蠕变试验中，样品横截面的变化是很小的，恒载荷往往就意味着恒应力；而在压痕蠕变试验中，随着压痕深度的变化，其接触面积也在变化，试验过程中应力和应变都在变化，使得压痕蠕变比拉伸蠕变复杂得多。
4.压痕松弛RIT
材料在保持恒压痕深度的情况下，试验力的相对变化量就为压痕松弛RIT，即
式中，P1为达到规定压痕深度的试验力；P2为压痕深度保持时间结束时的试验力。
在压痕松弛试验中，通过载荷控制系统的反馈，压痕深度保持恒定，由于压痕深度与应变相关，恒定的压痕深度就意味着恒定的应变，这就与传统上的应力松弛试验相类似，使得两者之间可以相互比较。
5.断裂韧性KC
按压痕硬度和弹性模量计算的方法，用Berkovich压头测得材料的压痕硬度值和压痕模量值，然后用Cube-corner压头进行压痕试验，由于Cube-corner压头比Berkovich压头尖得多，在周围材料中可产生较大的应力和应变，易于压痕裂纹的形成和扩展，如图6-16所示，测量在最大载荷F下的径向裂纹的长度C，则断裂韧性KC为
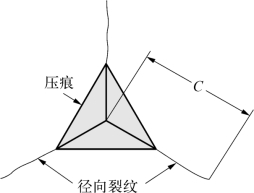
图6-16 Cube-corner压头在材料中产生径向裂纹
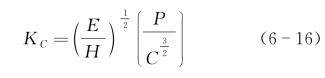
式中α为与压头形状相关的经验参数。一般情况下，即使用较小的载荷，Cube-corner压头也可在许多脆性材料中产生带有径向裂纹的亚微米压痕，因此，特别适合于薄膜或材料微小区域内的断裂韧性的测量。
6.连续刚度测试
由式6-11可以看到，计算得到的硬度和弹性模量都是最大载荷或最大压痕深度处所对应的硬度和弹性模量。Oliver等［65］提出了在加载过程中连续计算接触强度的动态测量方法。其原理是将相对较高频率的简谐力叠加在准静态的加载信号上，并测量压头的位移响应。简谐力的施加应保持在较小的水平上，以使在整个压入的过程中产生的简谐位移的振幅在一个很低的水平（1～2 nm），从而避免影响材料的变形过程。对接触强度进行连续测量，就可以利用一次压痕实验获得硬度和弹性模量随压痕深度的变化情况，这种技术称为连续刚度测量法（continuous stiffness measurement，CSM）。
图6-17为纳米压痕系统简图及其动力学模型。质量为m的压杆由刚度为Ks的两个弹簧支撑，弹簧的特点为在叶片平面内刚度很高而在垂直方向上刚度很低。带有压头的压杆被线圈—铁磁装置驱动，压头上的准静态载荷由加在线圈上缓慢变化的电流控制，再叠加小简谐分量。位移通过平行板电容器测量，运动被严格控制在一个自由度上。
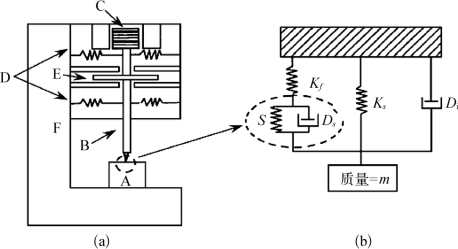
图6-17 纳米压痕系统简图及其动力学模型
A.试样；B.压杆；C.加载线圈；D.支撑；E.电容式位移传感器；F.加载框
为了计算接触刚度，压痕系统的动态响应必须确定。响应的分量为压头的质量m、支撑压头的两根弹簧的弹性系数Ks、压头框架的刚度Kf=1／Cf。Cf是载荷框架和阻尼系数C的联合响应量。阻尼系数C的出现是考虑到电容板位移传感器内有空气存在。
这些分量和接触刚度S一起产生全面的响应，如图6-17（b）所示。如果驱动力表示为P=Pos exp（iωt），压头的位移响应为h（ω）=h0 exp（iωt＋φ），则接触刚度S可以由位移信号中得出
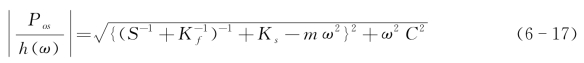
或者由力和位移信号的相差计算得出，位移角φ可以表示为
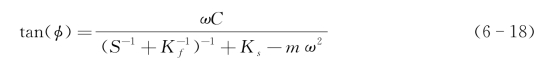
由式（6-17）和式（6-18）可以得出接触刚度S和空气在电容板间的阻尼系数ω（样品本身的阻尼可以忽略）
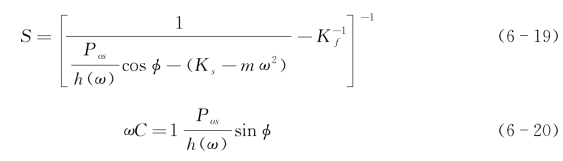
对于理想的玻氏压头来说，接触面积A是接触深度hc的函数，如式（6-10）所示。将式（6-11）代入式（6-6），可以得到
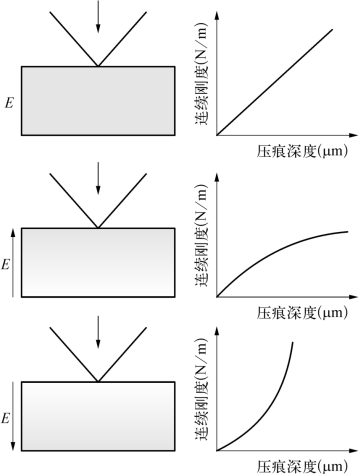
图6-18 均匀和梯度材料的连续刚度测量曲线
对于均质材料，由式（6-7）可知，其弹性模量E和Ei均为常数。则式（6-21）中接触刚度S与接触深度hc呈线性关系。而对于非均匀材料来说，E的值随着压痕深度而变化，在这种情况下，接触刚度S和接触深度hc的线性关系不成立。图6-18为均匀材料和梯度材料的压痕示意图。因此，CSM技术通过追踪接触刚度、弹性模量和硬度作为压痕接触深度函数的变化，能够用来研究梯度材料和多层结构的力学性能。对于大多数研究来说，普遍采用的是玻氏压头和45 Hz的振动频率。循环加载的幅度和所施加的最大载荷由所研究的材料决定。
有关纳米材料与结构测试方法的文章
- 详细阅读
-
纳米压痕仪的结构分析详细阅读
图6-19为一个商品化的纳米压痕仪及其工作原理。目前，各种商业应用的纳米压痕仪原理基本相同，它们的差别主要表现在力的加载方式和位移的测量方式上。图6-19压痕仪的结构及内部结构根据前面的介绍，目前的纳米压痕仪的工作模式有两种：普通模式和连续刚性测量模式。压头在纳米压痕仪中是一个重要的部件，测试时需要选择合适的压头。是纳米压痕试验另一个常用的压头。球形压头的初始接触应力小，仅产生弹性变形。......
2023-06-20
- 详细阅读
-
纳米压痕面阵列技术解析标记物运动详细阅读
通过使用装有Berkovich金刚石压头的仪器系统，我们可以在焊点横截面上制作一个纳米压痕标记物的面阵列。在本次研究中，所使用的纳米标记物的尺寸为5μm，标记深度为1 000 nm。图9.15所示为在电迁移试验前后，共晶锡银铜焊点横截面上所制成的纳米压痕标记物的阵列[15]。对于阳极附近标记物的反向移动，一种可能的机制是，背应力或柯肯达尔漂移引起了锡从阳极到阴极的反向流动。因此，为了分析第六行标志物的运动，我们需要一个不同的机制。......
2023-06-20
-
纳米压痕技术在应用中的优势和挑战详细阅读
近十几年来，在微观力学方面，纳米压痕技术受到越来越广泛的应用，主要体现在以下几个方面。图6-27为采用纳米压痕技术在硅表面施加50mN压力后形成的压痕阵列。图6-30为利用纳米压痕和显微成像技术相结合的一个典型例子。图6-31为采用材料纳米压痕技术测量Al多晶材料中一个晶粒性能的过程及力—位移曲线。Bahr［88］利用纳米压痕实验完成了低于50 nm深度的硬度测量；Adams［89］用纳米压痕实验研究了颗粒薄膜凝聚体的断裂机制。......
2023-06-20
-
如何结合纳米压痕仪和显微镜进行实验？详细阅读
从纳米压痕仪的结构可以看到，显微镜是压痕仪的重要组成部分，利用显微镜，可以精确定位需要测量的位置及实现对压痕、划痕等的观察。传统的纳米压痕仪通称使用光学显微镜。因此，现代的纳米压痕仪更多的是与各种高分辨率的显微镜相结合［67-72］。图6-25为压痕仪与扫描电镜、透射电镜和原子力显微镜相结。AFM纳米压痕的缺点是不能提供较大的载荷，响应速度较慢，数据处理复杂。......
2023-06-20
-
测试纳米材料磁学性能的优化方案详细阅读
纳米材料的磁性质主要表现为超顺磁性、高的矫顽力、低的居里温度和高的磁化率［1-3］。当纳米材料尺寸较小，使得各向异性减少到能与热运动相比拟时，磁化方向不再固定于一个易磁化方向而是做无规律的变化，因而出现超顺磁性现象。不同纳米材料出现超顺磁性的临界尺寸不同。由于小尺寸效应和表面效应而导致纳米粒子的本征和内在的磁性变化，使其具有较低的居里温度。......
2023-06-20
-
丁香烯的测试方法探究详细阅读
丁香烯从丁香叶油、丁香茎油、肉桂叶油等分离而得。有消炎止痛功能，可能还有一定的减压和治疗忧郁症的功能。从以上分子结构可以看出丁香烯是强非极性化合物，本方法用C18柱子加以分离及定量测试。②样品液的配制：称取一定量含有约10 mg丁香烯的样品，转入50 m L容量瓶中，加入10 m L水，超声5 min，再加入25 m L异丙醇，超声15 min，冷却后加入乙醇至刻度，摇匀后离心5 min，吸取清液即可注射。......
2023-07-02
相关推荐