1988年kass等人提出的基于能量函数的活动轮廓模型，即Snake模型，便是一种典型的自由式变形模板模型。Snake模型是一种有效地寻找目标轮廓的搜索算法，具有良好的提取、跟踪特定区域内目标边缘的能力，工作过程主要是利用能量最小化原理。实现Snake模型原型的算法通常十分复杂，曲线收敛速度慢且搜索范围有一定限制，因此许多学者提出了不同的算法，对经典Snake模型进行了改进。......
2023-11-24
基于原子力显微镜的测量技术优化方法
【摘要】：振动方法对材料无接触、无损伤，但是由于不能直接测量力，其应用仅限于弹性模量的测量。而基于显微镜的轴向加载需要的装置比较复杂。目前已报道了Si［50］、多晶Au［55］、Ag［57，58］、ZnO［53，59］等纳米线的弹性模量的实验结果。
振动方法对材料无接触、无损伤，但是由于不能直接测量力，其应用仅限于弹性模量的测量。而基于显微镜的轴向加载需要的装置比较复杂。相对而言，利用高精度微悬臂梁和位移探测系统的原子力显微术（AFM）能够以很高的分辨率同时实现空间尺寸（优于nm）和力信号（优于nN）的测量。因此，基于多种模式的AFM的实验纳米力学方法［48］很早即受到关注，并已逐渐发展成熟。
1.悬臂梁横弯曲
早在1997年，美国哈佛大学Lieber小组就利用原子力显微镜在侧向力模式下定量测量了单根SiC纳米线和多壁碳纳米管受到横向弯曲时的载荷—位移（Fd）曲线，并计算了它们的弯曲模量和强度。首先，他们将纳米线（管）分散在原子级平滑、摩擦系数很低的MoS2衬底上，然后沉积一层较厚的SiOx图形，那些正好有一端被压住的纳米线（管）就形成了图6-11（a）的水平悬臂梁构型；然后使用AFM进行定位并观察，再在沿SiC纳米线和碳纳米管长度方向不同的接触点处施加侧向力［图6-11（b）］，并记录侧向力对挠度的数据；最后考虑摩擦力、侧向集中力以及梁刚度的连续模型对数据进行分析。
根据F-d关系式（6-3）可知，通过拟合F-d曲线的斜率与x的关系既可得到弹性模量（弯曲模量）E。实验结果如图6-11（c）（d）所示，显示直径为23nm，悬臂梁长约600nm的SiC纳米棒的杨氏模量为610GPa，直径为21.5nm的SiC纳米棒的杨氏模量为660GPa，基本接近于在SiC体材料（111）方向的理论计算值600GPa。他们也测试了直径为32.9nm多壁碳纳米管的杨氏模量最大为1.26TPa，平均值为1.28±0.59TPa。通过连续施加载荷，他们还测试了SiC纳米线弯曲断裂前的最大弯曲强度和多壁碳纳米管出现屈曲前的最大弯曲强度分别是53.4GPa和14.2±8.0GPa。但是由于这种方法要求悬臂梁与衬底严格平行，也需要比较复杂的光刻工艺［50，51］，目前并未得到推广。
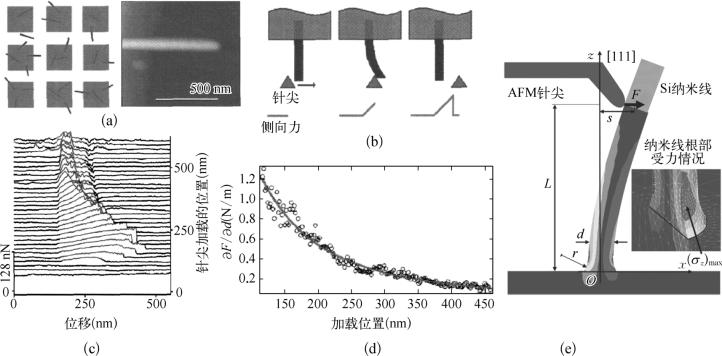
图6-11 F-d定量测试实验
（a）压在SiOx图形下的SiC纳米线及AFM图像 （b）用AFM针尖推动纳米线示意图（c）AFM测量的力曲线 （d）用式（6-3）拟合一系列x下测量的F-d曲线［49］ （e）针尖推动纳米线的变形模型［52］
根据悬臂梁弯曲至断裂之前所受的最大的力还可以计算纳米线（管）的断裂强度（σFS）。Lieber等报道的SiC纳米线的弯曲强度高达53.4 GPa，接近E／10的理论强度。2006年，Hoffmann等发展了SEM中的类似实验，如图6-11（e）所示，用纳米机械手的针尖推动悬臂梁构型的Si纳米线和ZnO纳米线［53］。根据断裂之前的最大挠度（S）能够计算纳米线根部受拉一侧的最大应变，也就是纳米线的弯曲断裂应变（σz）max，经过简单推导得到（D是纳米线的直径）
式中，E是杨氏模量。
2.三点弯曲
1999年，Salvetat等［54］发展了另一种通过Fd曲线测量弹性模量和断裂强度的方法。如图6-12（a）（b）所示，他们将多壁或单壁碳纳米管（SWCNT）束分散在多孔阳极氧化铝（AAO）表面，使CNT悬空于微孔上方，然后用AFM微悬臂的针尖在悬空部分的中点进行三点弯曲。假设范德华力足以使CNT的两端固定，则基于Timoshenko梁理论的Fd关系可写为
式6-5适用于短粗梁或CNT、WS2纳米管等剪切变形显著的层状结构；当L／D≫4
时，式6-4中只需要考虑纯弯曲的第一项，即简化为Euler-Bernoulli梁，大多数纳米线都符合这样的条件。此后的三点弯曲实验中更普遍的方法是利用光刻技术在硅衬底表面产生平行的沟槽，然后用聚焦离子束（FIB）辅助沉积铂（Pt），如图6-12（c）所示，从而确保纳米线两端的牢固固定。目前已报道了Si［50］、多晶Au［55］、Ag［57，58］、ZnO［53，59］等纳米线的弹性模量的实验结果。后来，王中林［60］和Eklund等［61］以沿纳米线轴向逐点测量Fd曲线代替仅在中点测量，可以消除因边界条件或加载位置不准确而产生的误差，进一步完善了三点弯曲方法。
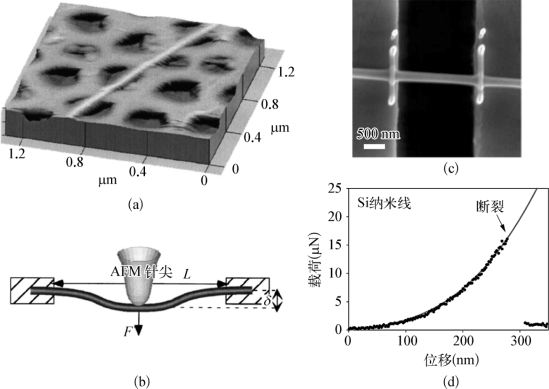
图6-12 各种纳米线弹性模量的测量
（a）搭在AAO微孔上CNT的AFM图像 （b）三点弯曲模型［54］（c）搭在沟槽上、两端固定的Au纳米线［55］ （d）一根Si纳米线弯曲过程的F-d曲线，直至断裂［56］
有关纳米材料与结构测试方法的文章
- 详细阅读
-
飞机水平测量技术优化方案详细阅读
飞机水平测量是飞机总装时对飞机各部件相对位置准确度进行检验和调整的工序。④飞机水平测量时，起落架应放下并锁住，机轮离地面50～100 mm。④水平测量应连续进行。中间间断2 h 以上时，必须重新复查飞机调平情况，然后才能继续测量。②飞机横向和纵向调平的误差一般为：0 mm±0.5 mm。水平测量图未规定时，则应符合HB/Z 103—1986《飞机水平测量公差》的要求。......
2023-07-18
-
基于内容的新闻推荐技术优化详细阅读
目前比较主流的推荐算法有基于协同过滤的推荐和基于内容的推荐等。由于协同过滤是根据用户对新闻的访问记录来进行推荐的，只有被阅读过的新闻才能被推荐，然而新闻的生命周期十分短暂，用户的访问矩阵会相当稀疏，这对于时效性要求比较高的新闻推荐系统是相当严重的缺陷，所以更多采用基于内容的推荐。大多数的基于内容的推荐系统在处理文字类item特征时，都会尝试将一篇文章映射到量空间模型。......
2023-06-28
-
技术测量基础及应用优化详细阅读
为保证测量的正确性，必须保证测量中单位的统一，为此我国以国际单单位制为基础确定了法定计量单位。测量精度是指测量结果与真值的一致程度。任何测量过程总是不可避免出现测量误差。量规检验不能获得被测几何量的具体数值。间接测量法存在基准不重合误差，故仅在不能或不宜采用直接测量的场合使用。......
2023-06-28
-
基于原位电子显微学的振动测量技术详细阅读
1996年，Treacy等在透射电子显微镜中首次发现，多壁碳纳米管的自由端因本征热振动而变得模糊［图6-1、］。进而，他们推导了热振动平均幅度与弹性模量和绝对温度的关系，从中估算，MWCNT的弹性模量可达1.8 TPa，接近于完美的石墨片的层内模量。Treacy等的报道因首次证实了CNT的超高弹性模量而受到普遍重视［7］。1999年，王中林教授等创新地提出了测量单根纳米线（管）弹性模量的原位电致振动方法。......
2023-06-20
-
视觉测量技术：影响测量系统精度的因素与提高方详细阅读
成像系统的几何畸变误差是典型的系统误差，是影响光学测量精度的因素之一。选用高质量的镜头和进行镜头畸变校正可提高测量精度。......
2023-11-24
-
电流测量电路优化方法详细阅读
电流测量有两种方法：直接测量法和间接测量法。低电压、小电流电路适合用直接测量法测量电流，高电压、大电流电路适合用间接测量法测量电流。测量直流电流要选择直流电流表，测量交流电流则要选择交流电流表。图2-4 利用电流互感器间接测量一相交流电流的电路使用钳形电流表也可以测量电路中的交流电流值。......
2023-06-15
-
基于规则的分类方法优化策略详细阅读
仔细研究各算法就会发现，决策树分类算法、关联规则分类算法、贝叶斯分类算法都是基于规则“A→C”和其统计特性的。C 4.5是决策树分类算法的代表[98]。构造决策树时，总选择增益比例大的属性作为下一分支节点。简化后的规则按类进行分组，形成最终的分类规则集。可见，贝叶斯分类器也是基于规则“A→C”的统计特性的。决策树分类法是一种直观且精度较高的方法，但决策树有时也会变得很复杂，以至于难以解释。......
2023-06-16
相关推荐